約数の個数と総和の公式・求め方が一目でわかる！なぜ？の証明もご紹介

約数の個数と総和の公式・求め方は高校数学の数学Aにおける重要な公式の1つです。

大学入試や共通テストでも頻出なので、必ず覚えておかなくてはなりません。

そこで今回は早稲田大学教育学部数学科を卒業した筆者が約数の個数と総和の公式・求め方について解説していきます。

なぜその公式・求め方なのか？の証明もご紹介しますので、数学が苦手な人はぜひ最後までお読みください。

約数の個数の公式・求め方

まずは約数の個数の公式・求め方から解説していきます。

自然数Nを素因数分解した結果がN=p^a×q^b×r^cとなるとき、

Nの正の約数の個数＝（a+1）（b+1）（c+1）[個]となります。

素因数分解とは、ある自然数を素数の掛け算のみで表すことです。

※素数とは何かについて解説した記事もぜひ合わせてご覧ください。

素数とは、約数が1とその数自身のみである自然数のことです。

例えば、7の約数は1と7（＝自分自身）のみなので素数となります。19の約数も1と19（＝自分自身）のみなので素数となります。

素因数分解のやり方は簡単です。例えば540を素因数分解してみましょう。

まずは素因数分解したい数（＝540）を書いて、それを素数で以下のようにどんどん割っていくだけです。

そして、英語の「L」になっている数（＝以下の図の赤字部分）を掛け合わせれば素因数分解の完了です。

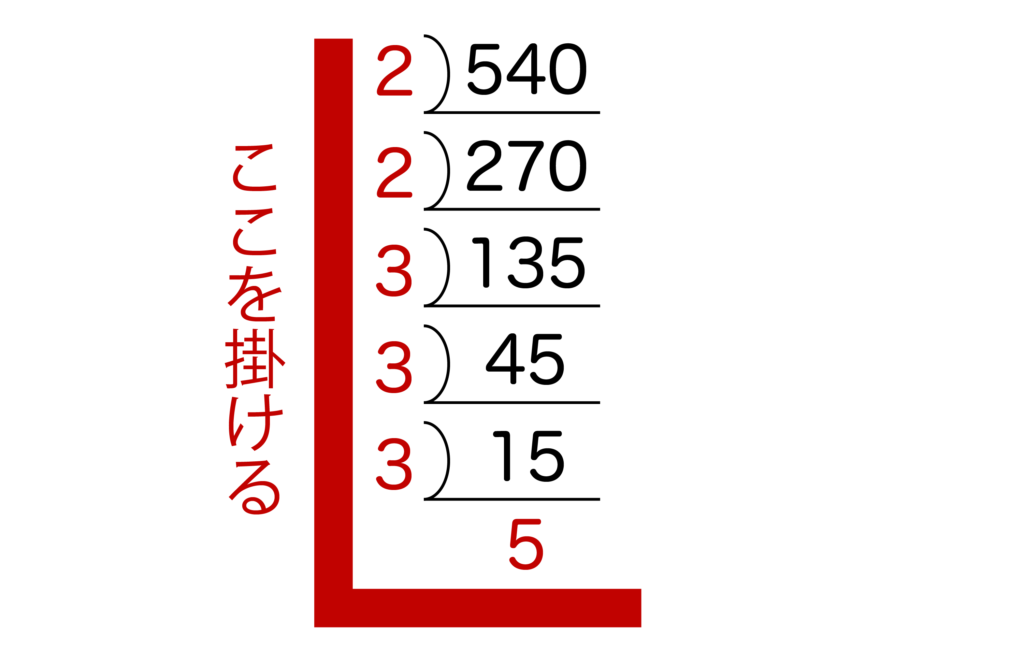
今回は2が2個と3が3個、5が1個あるので、540を素因数分解すると2²×3³×5となります。

2²=4、3³=27、5¹=5なので、4×27×5は確かに540になっていることが確認できます。

※素因数分解のやり方について詳しく解説した記事もぜひ参考にしてください。

では、以上を踏まえて540の正の約数の個数を求めてみましょう。

540を素因数分解すると2²×3³×5なので、540の正の約数の個数＝（2+1）（3+1）（1+1）＝3・4・2＝24[個]となります。

では、20の正の約数の個数はどうなるでしょうか？

20を素因数分解すると2²×5となりますね。

よって、20の正の約数の個数＝（2+1）（1+1）＝3・2＝6[個]となります。

実際に20の正の約数を書き出してみると、1、2、4、5、10、20なので確かに6個であることが確認できますね。

約数の個数の公式・求め方は難しくはないと思います。それぞれの数の指数に1を加えた数を掛け合わせるということを必ず覚えておきましょう。

約数の個数の公式・求め方の証明

では、なぜ自然数N=p^a×q^b×r^cとなるとき、Nの約数の個数＝（a+1）（b+1）（c+1）[個]となるのでしょうか？

先ほど使った540という数字で証明を行なっていきます。

540を素因数分解すると2²×3³×5でした。

なので、540の正の約数は

• a=0、1、2
• b=0、1、2、3
• c=0、1

として、2^a・3^b・5^cと表すことができますね。

aの定め方は3通りあり、そのおのおのについてbの定め方は4通り。さらに、そのおのおのについてcの定め方は2通りあるので、積の法則より540の正の約数の個数＝3×4×2＝24[個]となるわけです。

※積の法則とは何かについて解説した記事もぜひ合わせてご覧ください。

約数の総和の公式・求め方

続いては約数の総和の公式・求め方をご紹介します。

自然数Nを素因数分解した結果がN=p^a×q^b×r^cとなるとき、

Nの正の約数の総和＝（1+p+p²+・・・p^a）（1+q+q²+・・・q^b）（1+r+r²+・・・r^c）となります。

例えば、12を素因数分解すると2²×5でした。

なので、12の正の約数の総和＝（1+2+2²）（1+5）＝7・6=42となります。

20の正の約数を書き出してみると、1、2、4、5、10、20なので、

20の正の約数の総和＝1+2+4+5+10+20=42となり、確かに（1+2+2²）（1+5）と一致していることが確認できます。

また、先ほどから取り上げている540の正の約数の総和も求めておきましょう。

540を素因数分解すると2²×3³×5なので、

540の正の約数の総和＝（1+2+2²）（1+3+3²+3³）（1+5）＝7・40・6=1680となります。

約数の総和も個数と同じくそこまで複雑な公式ではないので覚えやすいと思います。

約数の総和の公式・求め方の証明

540をもとにして、自然数Nの正の約数の総和＝（1+p+p²+・・・p^a）（1+q+q²+・・・q^b）（1+r+r²+・・・r^c）[個]となることの証明を行なっていきます。

証明は非常に簡単です。

540の正の約数は（1+2+2²）（1+3+3²+3³）（1+5）・・・（※）を展開した項にすべて現れますね。

約数の総和は（※）を展開したときの項の数を求めることと同じになるわけです。

よって求める和は（1+2+2²）（1+3+3²+3³）（1+5）＝7・40・6となります。

なんだか不思議な感じの証明ですが、約数の総和に関する証明は大学入試や共通テストで出題される可能性は極めて低いので、そこまで重要視しなくても問題ありません。

しかし、約数の個数・総和の公式・求め方は必ず覚えておきましょう。

約数の個数・総和の公式が混乱したら

自然数N=p^a×q^b×r^cとなるとき

• 約数の個数＝（a+1）（b+1）（c+1）[個]
• 約数の総和＝（1+p+p²+・・・p^a）（1+q+q²+・・・q^b）（1+r+r²+・・・r^c）

でしたが、まだ公式に慣れていない人はどっちがどっちか混乱してしまう可能性もあるでしょう。

そんなときは、まずは両方（個数・総和）を求めてみてください。

ここで、約数の総和は必ずもとの自然数よりも大きくなるということを覚えておきましょう。

例えば、Nという自然数があったとき、Nは1とN（＝自分自身）は必ず約数に持ちます。

よって、N<N+1となります。当たり前ですが、約数の総和はもとの自然数よりも必ず大きくなるのです。

これを知っていれば、もとの数と個数・総和を比較して大き方が総和であることに気づけます。

つまり、小さい方は個数であるということになります。

例えば、先ほどから取り扱っている540に関しても、

• 540の正の約数の個数＝24
• 540の正の約数の総和＝1680

でした。どっちがどっちか迷ってしまっても、1680>540なので、1680が約数の総和であることがわかるというわけです。

約数の個数・総和を求める練習問題

最後に約数の個数・総和を求める練習問題をご用意しました。

公式を覚えるための練習だと思って解いてみてください。

【練習問題】

1400の約数の個数と総和を求めよ。また、1400の正の約数のうち偶数は何個あるかも求めよ。

【解答＆解説】

まずは以下のように1400を素因数分解しましょう。

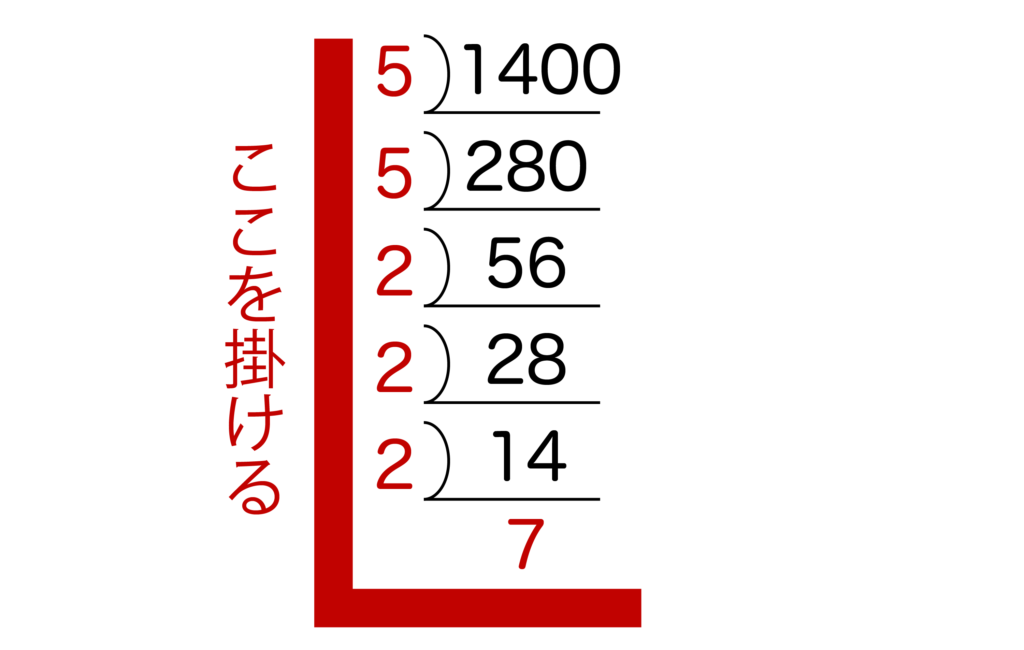
1400=2³・5²・7となりますね。

よって、1400の正の約数の個数＝（3+1）（2+1）（1+1）＝4・3・2＝24[個]・・・（答）となります。

1400の正の約数の総和＝（1+2+2²+2³）（1+5+5²）（1+7）＝15・31・8＝3720・・・（答）となります。

また、1400の正の約数のうち、偶数は

2^a・5^b・7^c（a=1、2、3； b=0、1、2； c=0、1）

と表すことができますね（ある数字に2の倍数をかければ、その数は必ず偶数になりますね）

aの定め方は3通りあり、そのおのおのについてbの定め方は3通り。さらに、そのおのおのについてcの定め方は2通りあるので、1400の正の約数のうち偶数であるものは3・3・2=18[個]・・・（答）となります。

今回は約数の個数と総和の公式・求め方とその証明について解説しました。

証明方法は最悪覚える必要はありませんが、公式・求め方は暗記必須です。教科書や参考書・問題集などでたくさんの練習問題を解いて慣れていってください。