本記事では高校数学の数学Aで登場する数珠(じゅず)順列を取り上げます。
数珠順列は円順列と似ており、違いがわからないという人も多いのではないでしょうか?
そこで今回は早稲田大学教育学部数学科を卒業した筆者が数珠順列とは何か・公式について解説した後、数珠順列の公式はなぜ2で割るのか?や円順列との違いなどについても解説していきます。
数学や場合の数が苦手な人でも理解できるように解説していくので、ぜひ最後までお読みください。
数珠順列とは?公式はなぜ2で割るのか?
異なるいくつかのものを円形に並べ、回転または裏返して一致するものは同じものであるとみなすとき、その並び方のことを数珠(じゅず)順列といいます。
例えば、以下2つの図は円順列としては異なるものとしてみなしますが、裏返すと同じものになるので、数珠順列においては以下の2つは同じものとみなすのです。
※円順列について詳しく解説した記事もぜひ合わせてご覧ください。
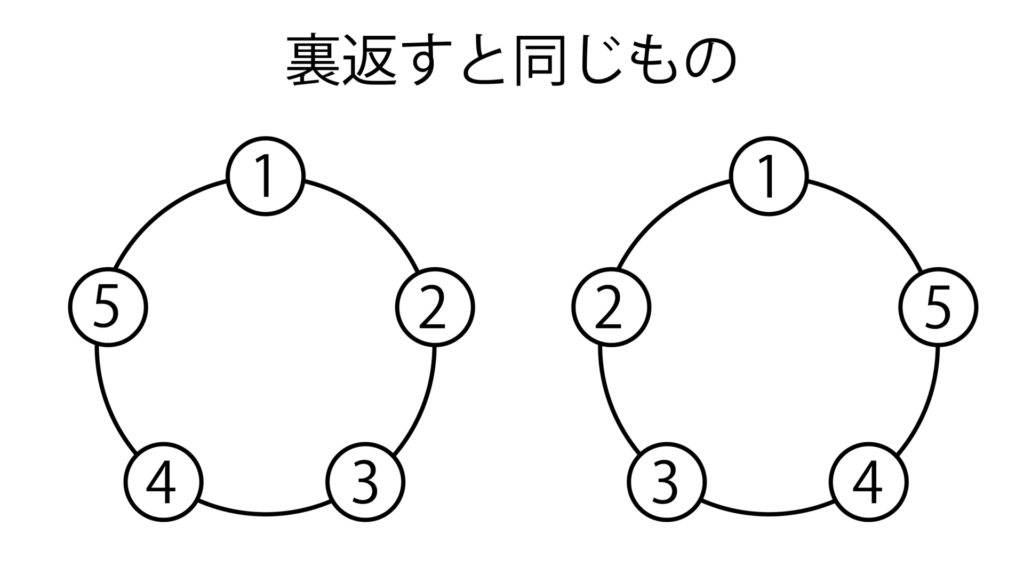
円順列の中には裏返すと一致するものが2つずつ存在するので、数珠順列の総数は円順列の総数の半分となります。
したがって、異なるn個のものの数珠順列の総数=円順列の総数/2=(n-1)!/2となります。
数珠順列の公式は円順列の公式とセットで覚えておきましょう。
※記号「!」の意味がわからない人は順列とは何かについて解説した記事をご覧ください。
数珠順列と円順列の違い
では、数珠順列と円順列の違いについて基礎問題をもとにして解説していきます。
以下の問題を解いてみましょう。
【問題】
異なる6個の宝石がある。このとき、以下の問いに答えよ。
(1)これらの宝石をテーブルの上で円形に並べる方法は何通りあるか求めよ。
(2)これらの宝石を使って首飾りを作るとき、何種類の首飾りができるか求めよ。
【解答&解説】
(1)用意された宝石をテーブルの上で円形に並べるので、裏返したりとかはできません。
したがって、これは円順列の問題となるので、(6-1)!=5!=120[通り]・・・(答)となります。
(2)首飾りとは首にかける装飾品のことで、宝石などをつないで輪にしたものです(以下は首飾りのイメージ)

首飾りは裏返すと同じものになるので、円順列ではなく数珠順列となります。
したがって(6-1)!/2=60[種類]・・・(答)となります。
問題文に首飾りやネックレス、ブレスレット、腕輪など裏返すことができるものが現れたときは数珠順列を疑いましょう。
円順列と数珠順列の違いは、
- そもそも裏返すことができるかどうか?できるなら数珠順列
- 数珠順列では、裏返して一致するものは同じものとみなす
の2点です。混乱する人が多いので必ず覚えておきましょう。
数珠順列の練習問題(応用問題も)
数珠順列の公式を理解したところで、数珠順列の練習問題を2問解いてみましょう。応用問題も用意しています。
【練習問題】
(1)異なる色のガラス玉8個を輪にしてブレスレットを作るとき、玉の並び方の異なるものは全部で何通りあるか求めよ。
(2)立方体の各面に、隣り合った面の色は異なるように色を塗る。このとき、異なる5色をすべて使って塗る方法は何通りあるか求めよ。
ただし、立方体を回転させて一致する塗り方はすべて同じものとみなす。
【解答&解説】
(1)ブレスレットという言葉が登場しているので数珠順列を疑いましょう。
ブレスレットは裏返すと同じものになるので円順列では数珠順列となります。
よって数珠順列の公式より、(8-1)!/2=2520[通り]・・・(答)となります。
(2)数珠問題の応用問題となります。立方体は全部で6面ありますが、色は5色しかありません。
5色の場合、同じ色の面が必ず2つ登場します。その色の選び方は5通りです。その色でまずは上面と下面を塗って固定しましょう。
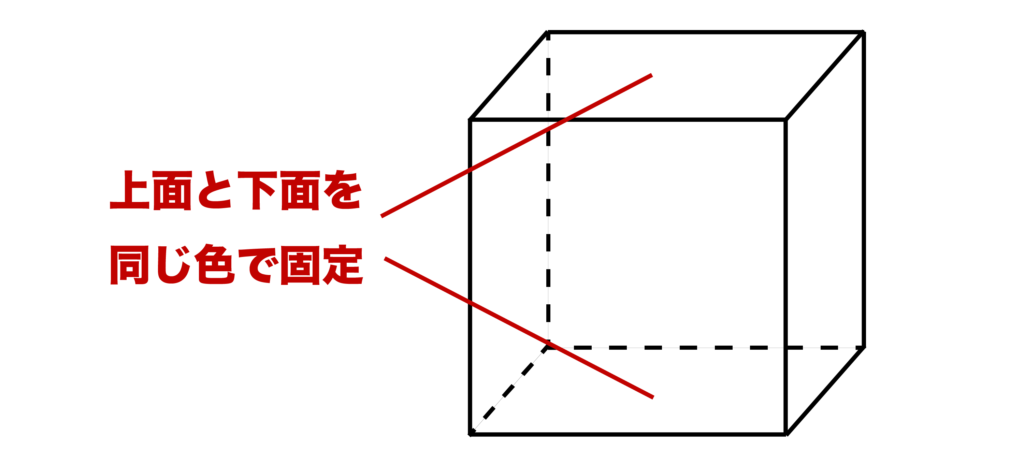
すると、そのおのおのについて側面の塗り方には上下をひっくり返すと塗り方が一致する場合が含まれていますね。
※例えば、色を1〜5とした場合、以下の図のような2つの塗り方(側面の色の並び方が時計回り、反時計回りの違い)は上下をひっくり返すと一致しますね。
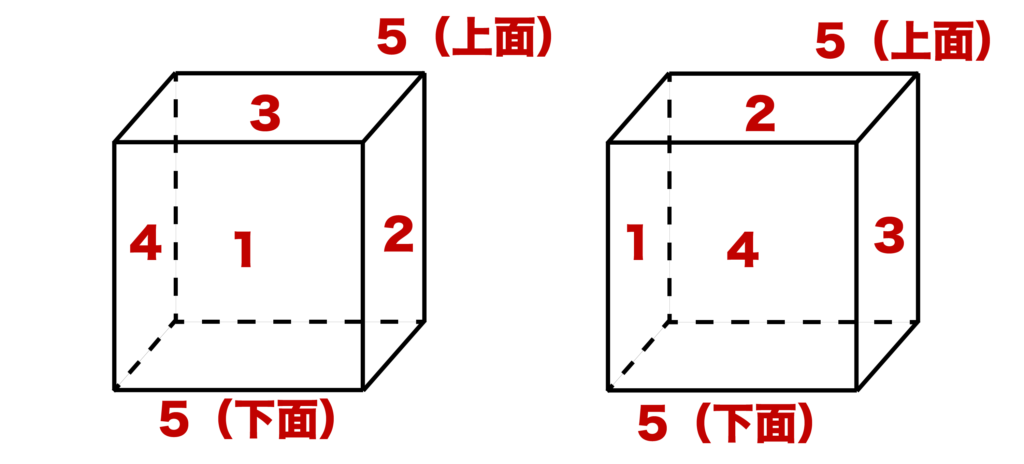
つまり、異なる4つの数珠順列となるので(4-1)!/2=3[通り]
したがって、求める総数は5・3=15[通り]・・・(答)となります。
今回は数珠順列とは何か・数珠順列の公式はなぜ2で割るのか?について解説した後、円順列との違いや練習問題をご紹介していきました。
繰り返しにはなりますが、裏返せるか?裏返すと同じになるか?の2点を意識して円順列との違いを見極めていきましょう。


