中点連結定理は中学数学で学習しますが、高校の教科書によっては数学Aで中学数学の復習として簡単に中点連結定理を取り上げているものもあります。
なので、本記事でも簡単に中点連結定理を振り返っておきます。
今回は早稲田大学教育学部数学科を卒業した筆者が中点連結定理とは何か・なぜ中点連結定理は成り立つのか(証明)や、中点連結定理の逆などについて解説します。
台形の中点連結定理についても解説している充実の内容なので、ぜひ最後までご覧ください。
中点連結定理とは?
まずは中点連結定理とは何かについて解説します。
中点連結定理とは以下の図のように三角形ABCがあるとき、辺AB、ACの中点をそれぞれ点M、Nとすると、
- MN//BC(MNとBCは平行)
- MN=BC/2(MNはBCの半分の長さ)
が成り立つことです。
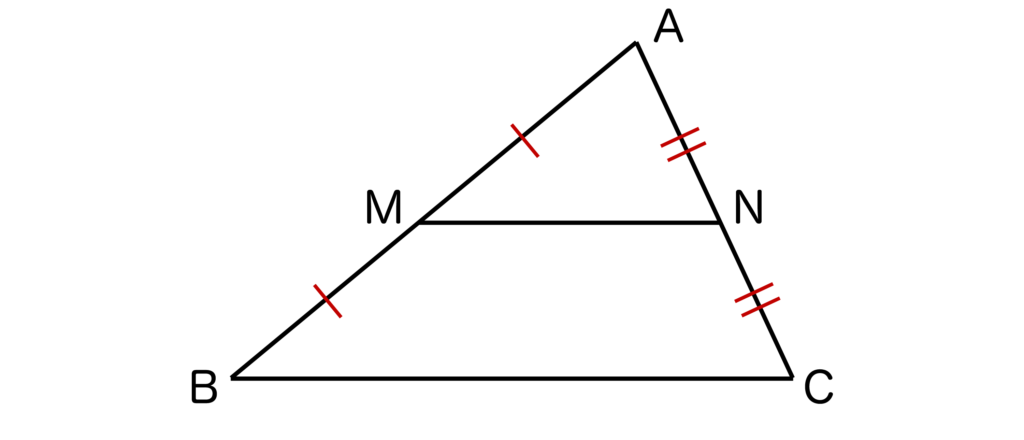
例えば、上記の三角形ABCにおいて、BC=10cmだとすると、MN=10/2=5[cm]となります。
以上が中点連結定理とは何かについての解説となります。中点連結定理自体はとても簡単な公式だと思います。
中点連結定理の証明2つ
では、中点連結定理はなぜ成り立つのでしょうか?ここからは中点連結定理が成り立つ理由(証明)を行なっていきます。
今回は2つの証明方法を取り上げます。
証明1:相似の活用
中点連結定理の証明方法1つ目は相似を活用することです。
以下の三角形ABCにおいて、三角形ABCと三角形AMNに注目します。
すると、
- ∠Aは共通
- AB:AM=2:1
- AC:AN=2:1
より、2組の辺の比とその間の角がそれぞれ等しいので、三角形ABCと三角形AMNは相似になります。
※三角形の相似条件を忘れてしまった人は三角形の相似条件について解説した記事をご覧ください。

よって、三角形ABCと三角形AMNの相似比=2:1となります。
したがって、BC:MN=2:1となるので、MN=BC/2が証明できました。
また、三角形ABCと三角形AMNが相似であることから∠ABC=∠AMNが成り立ちます。
よって、同意角が等しいのでMNとBCが平行であることが証明できました。
※同意角がわからない人は対頂角・同位角・錯角とは何かについて解説した記事をご覧ください。
証明2:平行四辺形の活用
中点連結定理の証明方法2つ目は平行四辺形の性質を活用することです。
以下の図のように三角形ABCにおいて、MNの延長線上にMN=NDとなる点Dをとります。
そして、AD、CD、MCを結びます。
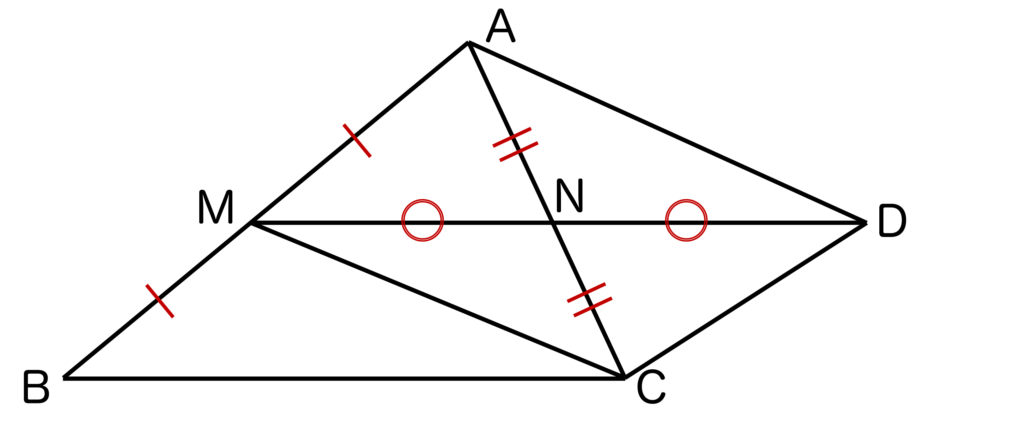
このとき、四角形AMCDに注目すると
- MN=ND
- AN=NC
より、対角線がそれぞれの中点で交わるので、四角形AMCDは平行四辺形となることがわかります。
よって、
- AM=CD
- AM//CD・・・①
となります。
また、四角形MBCDに注目すると、
①より、MB//CD・・・②
AM=MBよりMB=CD・・・③
となります。②、③より、1組の対辺が平行かつ長さが等しいので、四角形MBCDは平行四辺形であることがわかります。
よって、MN//BCが証明できました。
また、MD=BCとMN=MD/2より、MN=BC/2も証明できました。
中点連結定理の逆とは?
ここからは中点連結定理の逆とは何かについて解説します。
中点連結定理の逆とは、以下の図のように三角形ABCの辺AB上の点Mと、辺AC上の点Nについて、
- MN//BC
- MN=BC/2
であれば、点M、Nはそれぞれ辺AB、ACの中点になるということです。
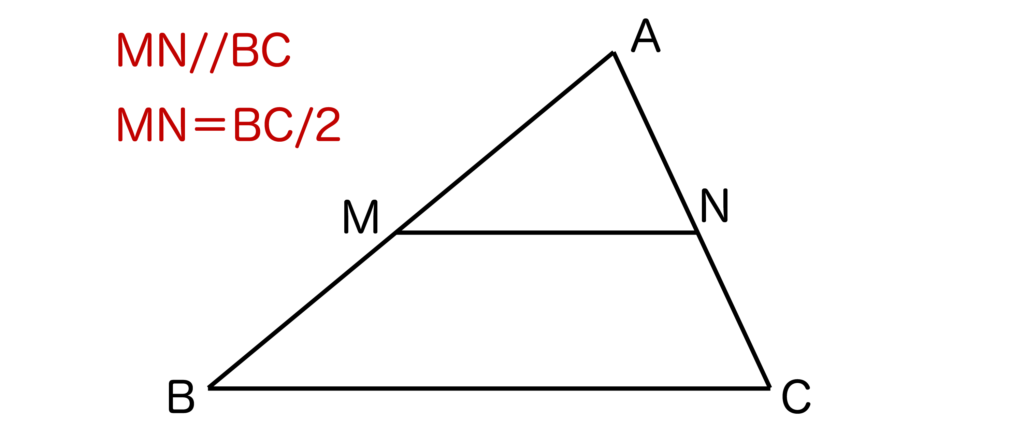
以上が中点連結定理の逆とは何かの解説となります。
中点連結定理の逆の証明
中点連結定理の逆が成り立つ理由も、先ほどと同じように三角形の相似を使って証明が可能です。
【証明】
以下の図において、三角形ABCと三角形AMNに注目します。

このとき、MN//BCより同意角は等しいから
- ∠ABC=∠AMN
- ∠ACB=∠ANM
となります。よって、2組の角がそれぞれ等しいので三角形ABCと三角形AMNは相似となります。
ここで、BC:MN=2:1であることから三角形ABCと三角形AMNの相似比は2:1であることがわかります。
したがって、
- AB:AM=2:1
- AC:AN=2:1
となるので、点M、Nはそれぞれ辺AB、ACの中点であることが証明できます。
【証明終】
中点連結定理と三角形の相似は非常に相性が良いので必ず使えるようにしておきましょう。
台形の中点連結定理とは?
中点連結定理は三角形だけでなく、台形にもあります。
台形の中点連結定理とは以下の図のように台形ABCDがあったとき、辺AB、DCの中点をそれぞれ点M、Nとすると、AD//BCであれば
- MN//BC
- MN=(AD+BC)/2
が成り立つことです。
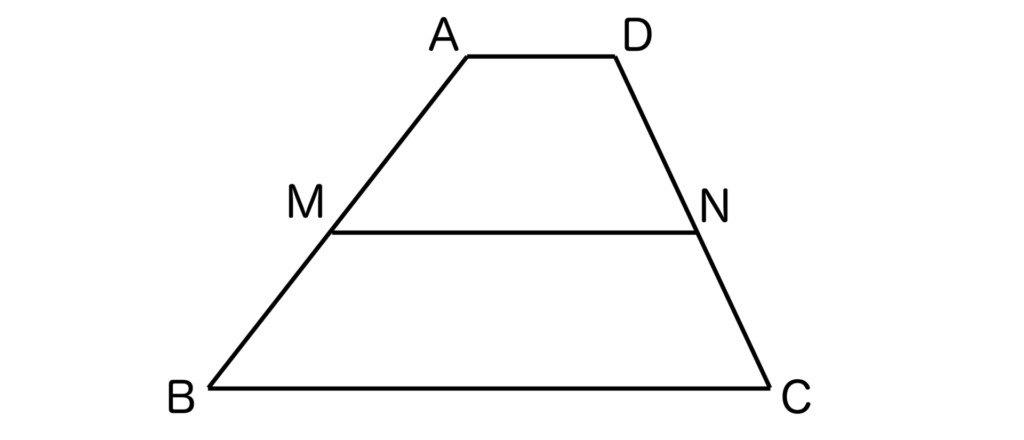
例えば、上記の台形ABCDにおいて、AB=5cm、BC=9cmの場合、MN=(5+9)/2=7[cm]となります。
台形の中点連結定理も非常に重要ですので必ず覚えておきましょう。
台形の中点連結定理の証明
ここからは台形の中点連結定理が成り立つ理由(証明)について解説していきます。
【証明】
以下の台形ABCDにおいて、ANの延長線とBCの延長線が交わる点をDとします。
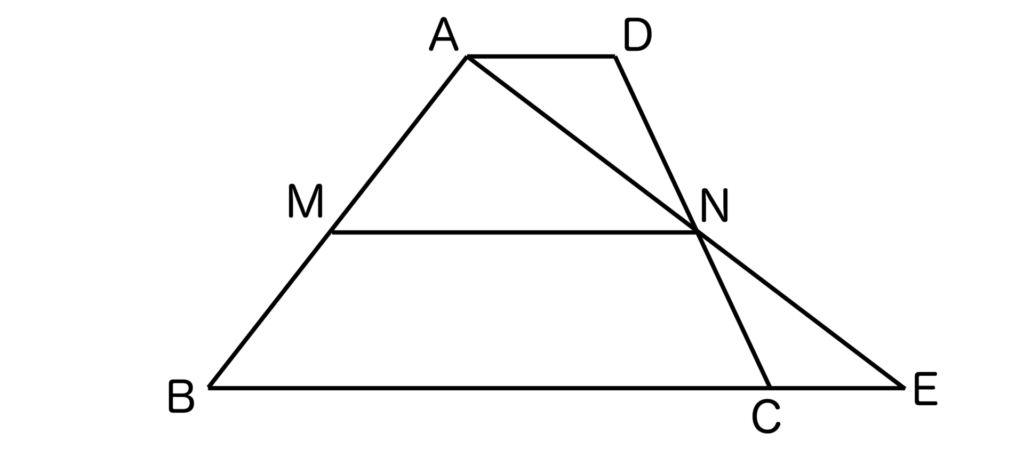
ここで、三角形NDAと三角形NCEに注目すると、点NはACの中点なのでAN=EN・・・①です。
対頂角は等しいので∠AND=∠ENC・・・②です。
また、AD//BCより錯角は等しいので∠NDA=∠NCE・・・③です。
①〜③より1辺とその両端の角がそれぞれ等しいので、三角形NDAと三角形NCEは合同となります。
※三角形の合同条件を忘れてしまった人は三角形と直角三角形の合同条件について解説した記事をご覧ください。
よってAN=EN、AD=ECとなります。
ここで、三角形ABEに注目するとAN=ENより点Nは辺AEの中点であることがわかります。
BE=BC+CEなので、AD=ECより、BE=BC+ADとなります。
点M、Nはそれぞれの辺AB、GAの中点なので、中点連結定理より、BE=2MNです。
よって、2MN=BC+ADとなるので、MN=(AD+BC)/2が証明できました。
中点連結定理と四角形の関係・証明
中点連結定理を活用すると、四角形の中点を結ぶと平行四辺形になるということを証明することも可能です。
例えば以下の図のように四角形ABCDにおいてAB、BC、CD、DAの中点をそれぞれ点E、F、G、Hとすると、四角形EFGHは平行四辺形となります。
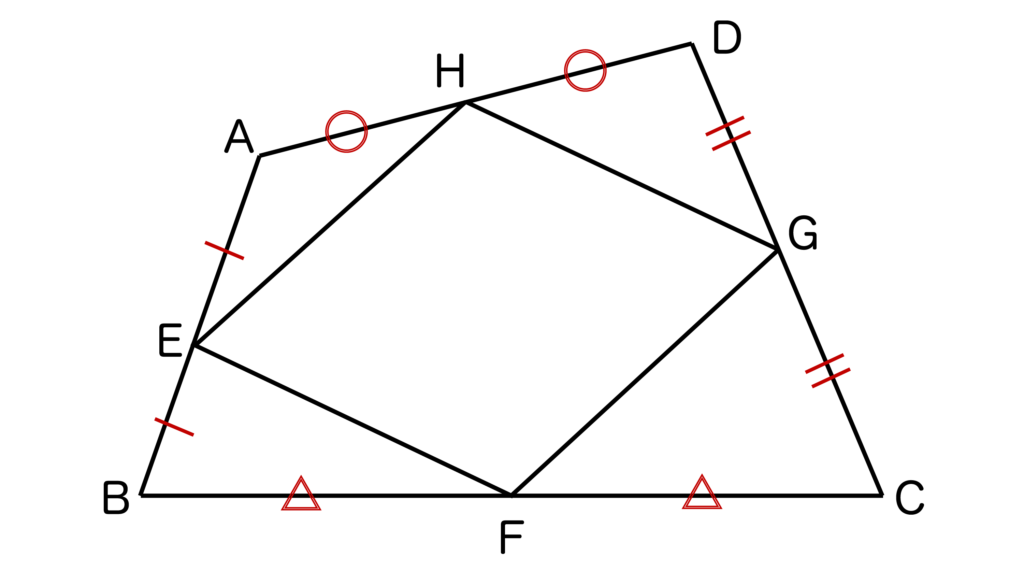
以上が成り立つことの証明を行なっていきます。
【証明】
上記の四角形ABCDにおいて、以下のように対角線ACを引きます。
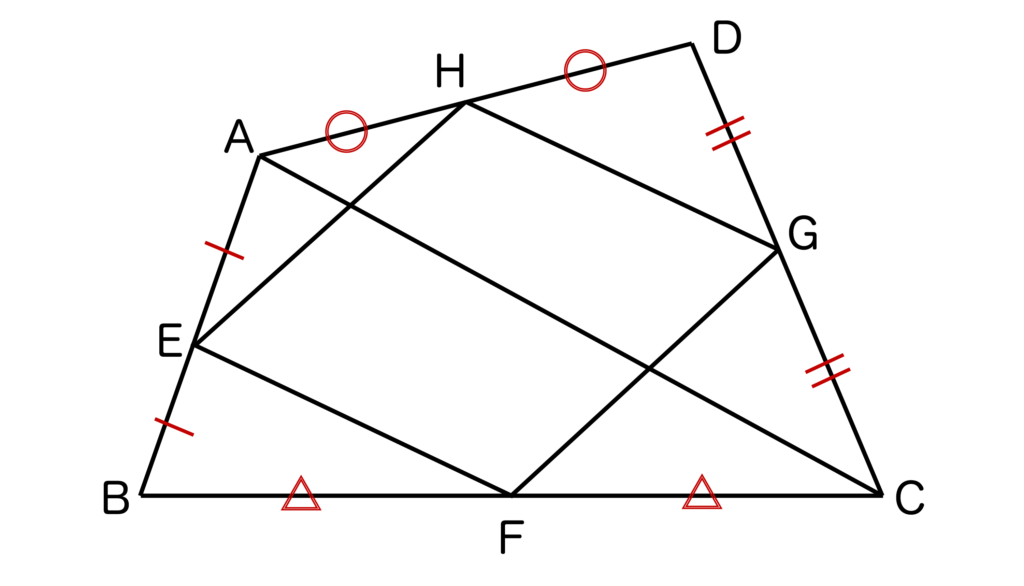
三角形ABCにおいて点E、FはそれぞれAB、BCの中点なので、中点連結定理より
- EF//AC・・・①
- EF=AC/2・・・②
が成り立ちます。
また、三角形ACDにおいて、点G、HはそれぞれCD、DAの中点なので、中点連結定理より、
- HG//AC・・・③
- HG=AC/2・・・④
が成り立ちます。
- ①、③より、EF//HG・・・⑤
- ②、④より、EF=HG・・・⑥
となるので、⑤⑥より、1組の対辺が平行かつ長さが等しいので、四角形EFGHは平行四辺形であることが証明できました。
【証明終】
ちなみにですが、四角形ABCDが長方形の場合はひし形、正方形の場合は正方形となります。
以下の図は長方形ABCDですが、四角形EFGHはひし形となります。
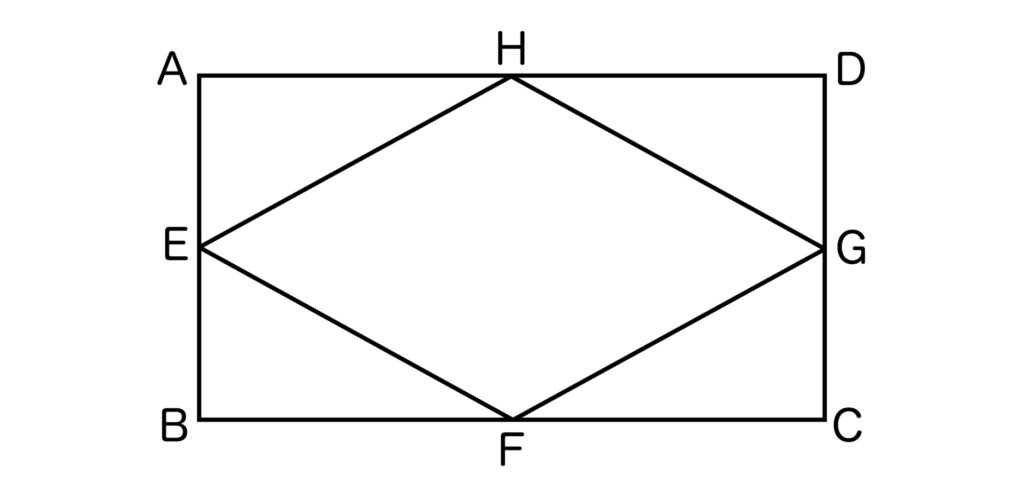
中点連結定理と四角形の関係も非常に重要なので必ず頭に入れておきましょう。
中点連結定理の練習問題
最後に中点連結定理の練習問題をご紹介します。
基礎的な問題なので、必ず解けるようにしておきましょう。
【問題】
以下の三角形ABCにおいて、点D、Eは辺ABを3等分する点とする。また、BCの延長と点Dを通り、ECに平行な直線との交点をFとする。また、ACとDFの交点をGとする。
GF=10のとき、DGの長さを求めよ。
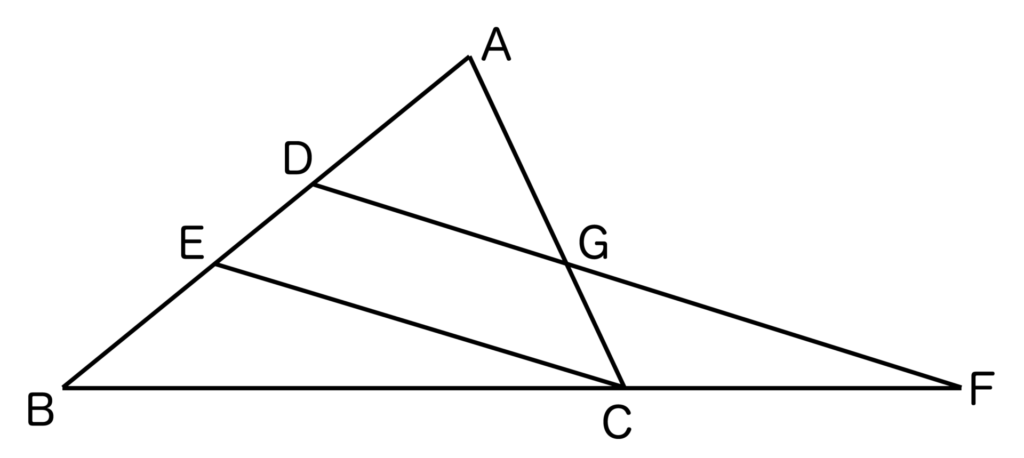
【解答&解説】
DGの長さをxとおきます。
すると、三角形AECにおいて中点連結定理が成り立つので、EC=2xとなりますね。
また、三角形BDFにおいても中点連結定理が成り立つので、
DF=2×EC=4xとなります。
また、問題文よりGF=10で、DG=xなので、DF=10+xとも表すことができます。
よって、4x=10+xという方程式ができあがるので、3x=10よりx=10/3・・・(答)となります。
いかがでしたか?
今回は中点連結定理とは何かについて解説した後、中点連結定理の証明や逆・台形パータンもご紹介していきました。
中点連結定理は図形問題を解く上で必須の知識の1つです。必ず理解しておきましょう。


