二次関数の最大値・最小値は二次関数の分野の中でも苦戦する人が多いです。特に変域(定義域・値域)が絡んでくるとより苦戦する人が多くなります。
しかし、二次関数の最大値・最小値はしっかりと図を書けばそこまで難しくはありません。
今回は早稲田大学教育学部数学科を卒業した筆者が二次関数の最大値・最小値について図解でわかりやすく解説します。また、変域が指定されているときの二次関数の最大値・最小値についても解説します。
二次関数の最大値・最小値(基本事項)
まずは二次関数の最大値・最小値の基本事項から解説します。
y=ax2+bx+cという二次関数があったとき、それがy=a(x-p)2+qに平方完成できるとしましょう。
※平方完成については二次関数の平方完成の公式・やり方をご紹介した記事をご覧ください。
このとき、頂点の座標は(p、q)となりますね(理由がわからない人は二次関数の頂点について解説した記事をご覧ください。)
a>0のとき、二次関数のグラフは下に凸な形となり、x=pで最小値qとなります。最大値はありません。
※下に凸がわからない人は二次関数のグラフの作成方法を解説した記事をご覧ください。
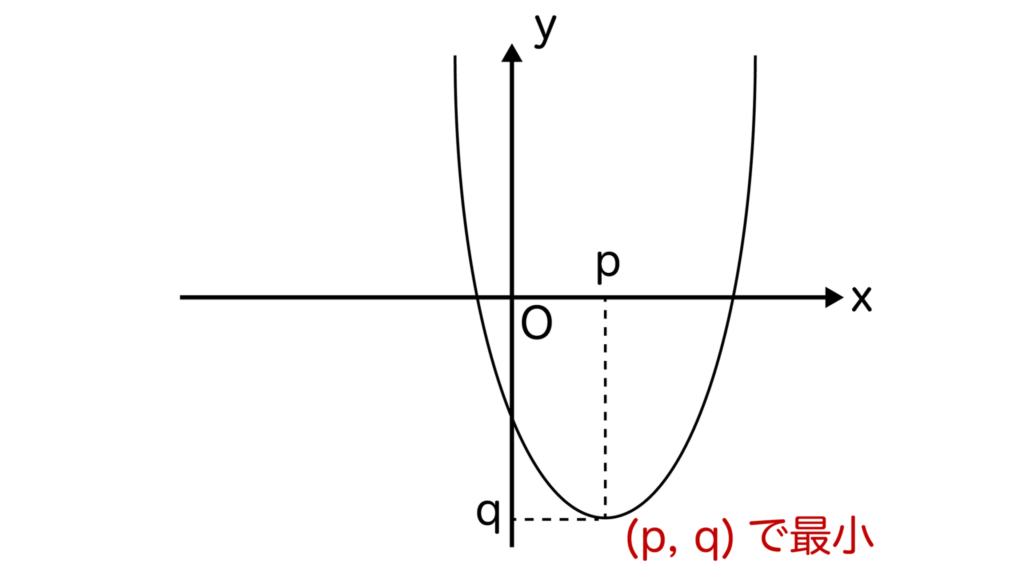
最大値がない理由ですが、下に凸な形な二次関数のグラフはx軸が左右に永遠に続いており、それに伴ってyの値も永遠に増加するからです。
逆に、a<0のとき、二次関数のグラフは上に凸な形となり、x=pで最大値qとなります。最小値はありません。
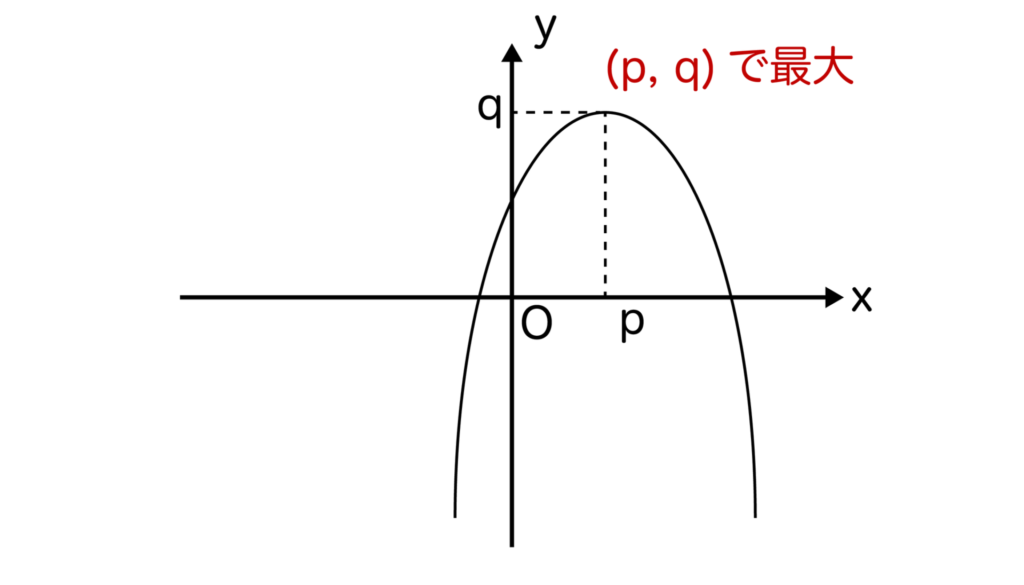
つまり、二次関数は定義域が実数全体のとき、a>0ならば最小値、a<0ならば最大値を持ち、それはグラフの頂点のy座標となります。
※定義域=xの変域のことです。詳しくは一次関数の変域について解説した記事をご覧ください。
※実数がわからない人は、実数とは何かについて解説した記事をご覧ください。
二次関数の最大値・最小値(基本問題)
以上を踏まえて、二次関数の最大値・最小値に関する基本問題を解いてみましょう。
【例題】
以下の二次関数における最大値・最小値を求めよ。
(1)y=x2+6x+10
(2)y=-x2+2x+5
【解答&解説】
(1)y=x2+6x+10を平方完成すると、(x+3)2+1となりますね。
よって、頂点の座標は(-3、1)です。y=x2+6x+10は下に凸なグラフなので、
x=-3で最小値=1、最大値はなし・・・(答)となります。
(2)y=-x2+2x+5を平方完成すると、-(x-1)2+6より、頂点の座標は(1、6)です。
y=-x2+2x+5は上に凸なグラフなので、
x=1で最大値=6、最小値はなし・・・(答)となります。
問題文に記載がなくても、最大値・最小値を求める問題では、それらを与えるxの値を明示するのが原則となりますのでぜひ覚えておきましょう。
二次関数の最大値・最小値(変域があるとき)
ここからは変域があるときの二次関数の最大値・最小値について解説します。
先ほどと同様に、y=ax2+bx+cという二次関数があったとき、それがy=a(x-p)2+qに平方完成できるとします。
そして、定義域としてh≦x≦kが与えられているとしましょう。
※記号「≦」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。
この場合、最大値・最小値は軸x=pの位置によって以下のように変わります(5パターンあります)
※今回はa>0として解説していきます。
その1:軸が定義域の右外
軸が定義域の右外とは以下のような状態です。
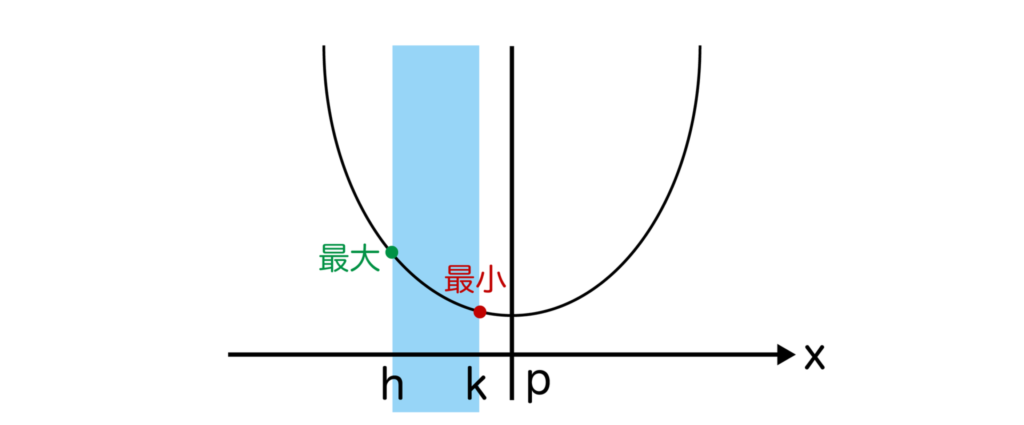
この場合、x=hで最大、x=kで最小となります。
その2:軸が定義域内かつ定義域の右寄り
軸が定義域内かつ定義域の右寄りとは以下のような状態です。
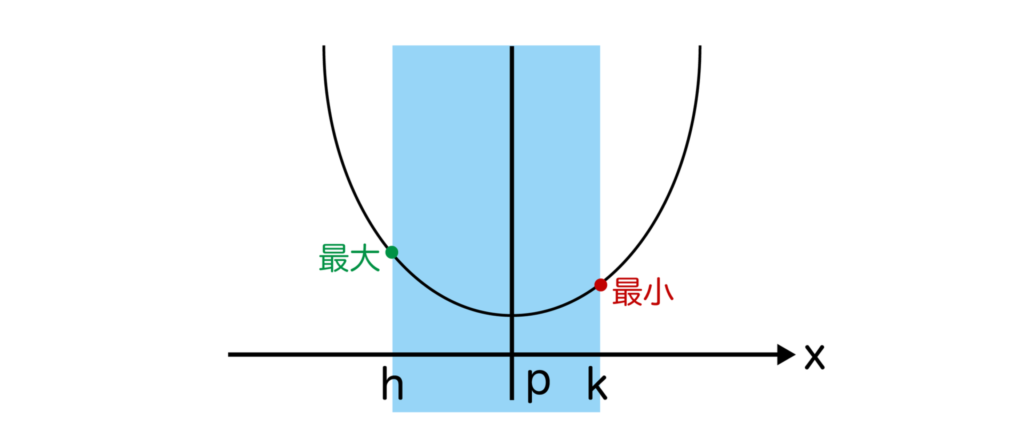
この場合、x=hで最大、x=pで最小となります。
※二次関数のグラフは軸に関して左右対称なので、軸がkに近い側にあると、x=kよりもx=hの方が大きい値を取ります。
その3:軸が定義域内かつ定義域の中央
軸が定義域内かつ定義域の中央とは以下のような状態です。
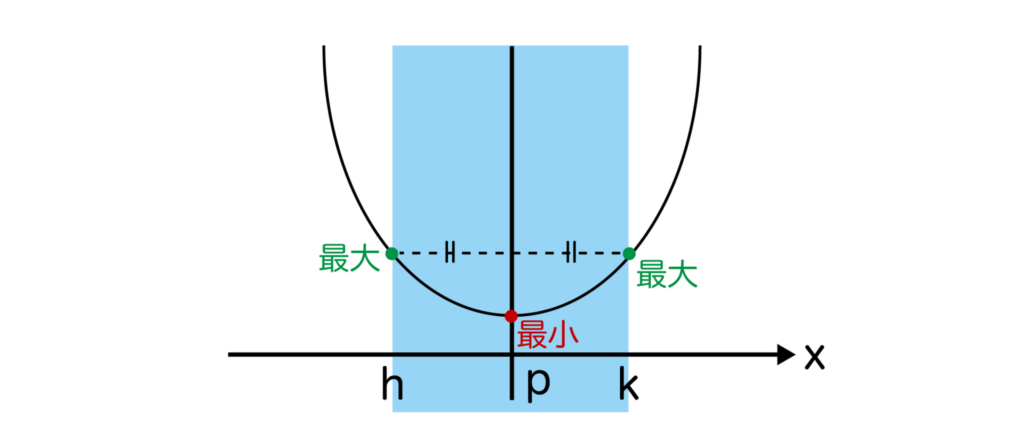
この場合、x=h、kで最大、x=pで最小となります。
軸が定義域の中央にあるため、x=hのときのyの値と、x=kのときのyの値が等しくなります。
その4:軸が定義域内かつ定義域の左寄り
軸が定義域内かつ定義域の左寄りとは以下のような状態です。
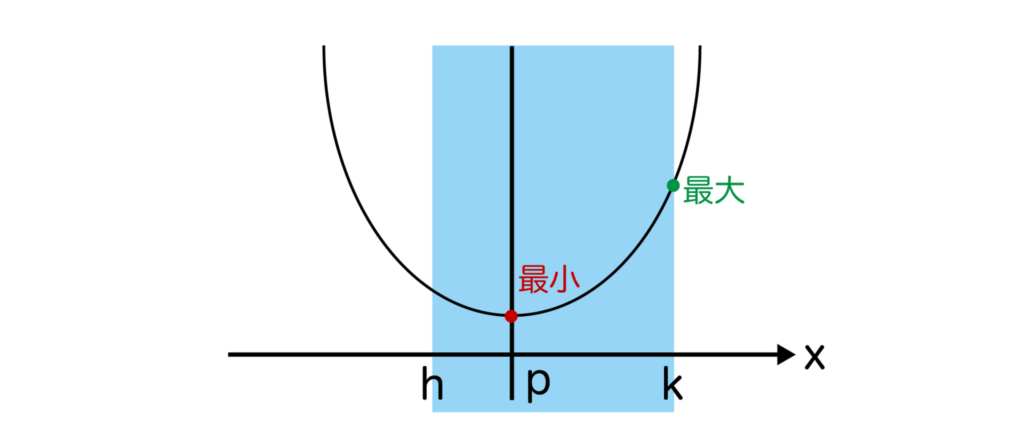
この場合、x=kで最大、x=pで最小となります。
先ほども解説した通り、二次関数のグラフは軸に関して左右対称なので、軸がhに近い側にあると、x=hよりもx=kの方が大きい値を取ります。
その5:軸が定義域の左外
軸が定義域の左外とは以下のような状態です。
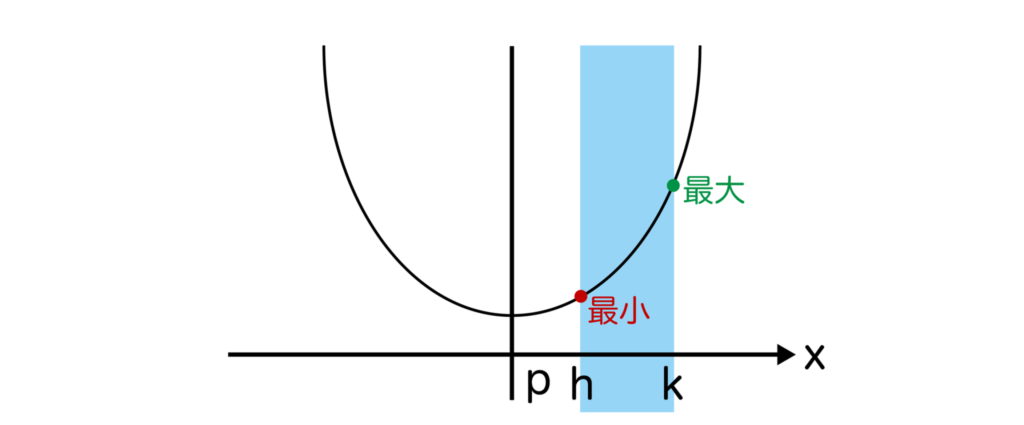
この場合、x=kで最大、x=hで最小となります。
以上が定義域が与えられているときの二次関数の最大値・最小値5パターンです。
a<0の場合はグラフが上に凸となり、最大と最小が入れ替わるだけです。
以上のように、定義域が与えられているときは二次関数の頂点・軸がどこにあるのか?をしっかりと意識することが重要です。グラフを書くなどして対策しましょう。
二次関数の最大値・最小値の問題(変域があるver)
以上を踏まえて、変域(定義域)がある場合の二次関数の最大値・最小値の問題を1つ解いてみましょう。
【例題】
以下の二次関数の最大値・最小値を求めよ。
(1)y=2x2-8x+5(0≦x≦3)
(2)y=-x2-2x+2(-3<x≦-2)
【解答&解説】
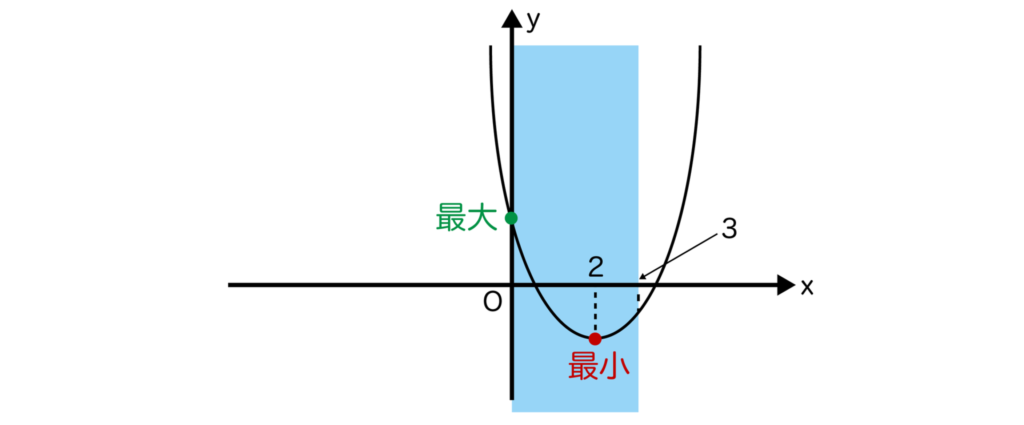
(1)2x2-8x+5を平方完成すると、2(x-2)2-3となるので、頂点の座標は(2、-3)です。
頂点のx座標が定義域0≦x≦3の範囲内にあるので、x=2のとき最小値=-3・・・(答)となります。
また、頂点のx座標は定義域0≦x≦3の3よりにあるので、x=0のとき最大値=5・・・(答)となります。
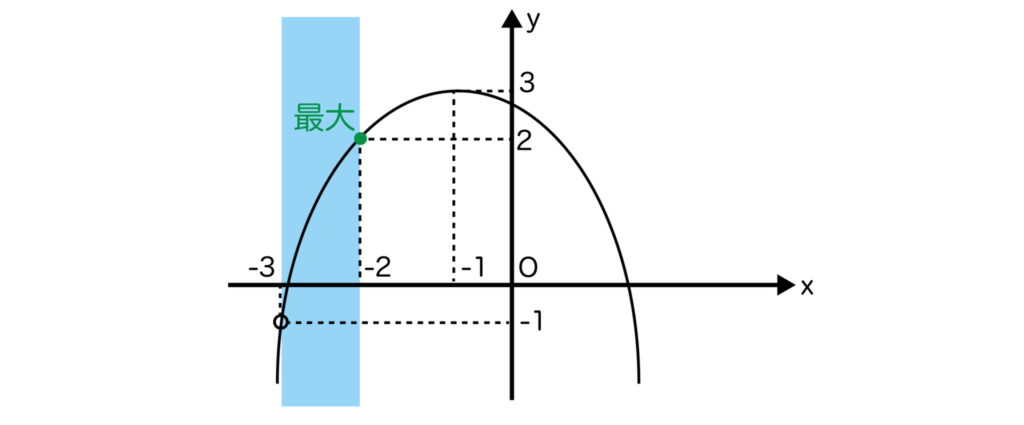
(2)-x2-2x+2を平方完成すると-(x+1)2+3となるので、頂点の座標は(-1、3)です。
頂点のx座標は定義域-3<x≦-2の右外にあるので、x=-2のとき最大値=-(-2)2-2×(-2)+2=2・・・(答)となります。
-3<x≦-2より、x=-3は定義域に含まれないので、最小値はなし・・・(答)となります。
二次関数の最大値・最小値の問題(変域に文字があるver)
ここからは応用問題となります。まずは変域に文字があるバージョンの問題です。
【問題】
aを正の定数としたとき、二次関数y=x2-4x+5(0≦x≦a)について以下の問いに答えよ。
(1)最小値を求めよ。
(2)最大値を求めよ。
【解答&解説】
(1)x2-4x+5を平方完成すると(x-2)2+1ですね。つまり頂点は(2、1)となります。
軸x=2が変域0≦x≦aに含まれるかどうかで場合分けを行いましょう。
[1]0<a<2のとき
以下の図のように、軸x=2は変域の右外にあるのでx=aで最小となります。
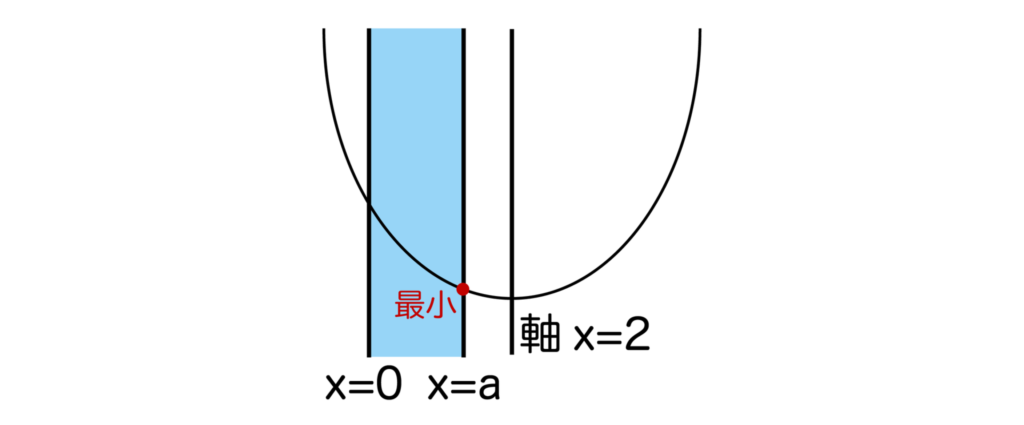
よって最小値=a2-4a+5となります。
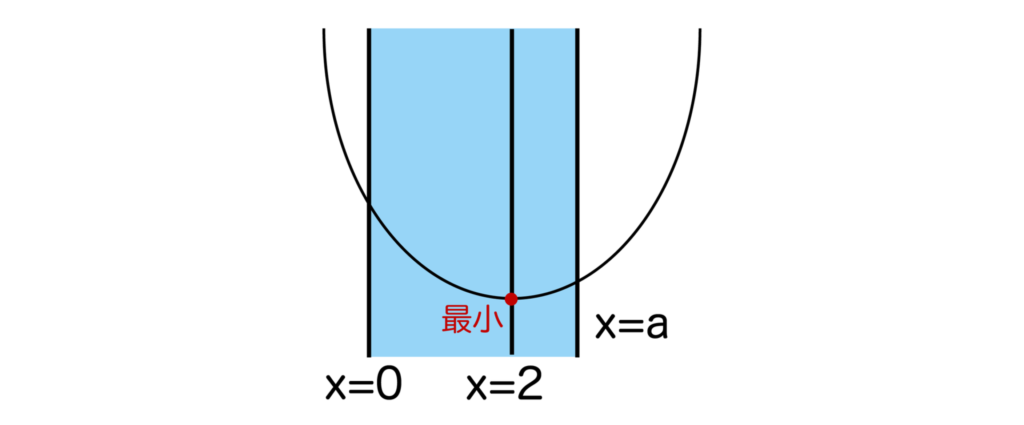
[2]a≧2のとき
以下の図のように、軸x=2は変域の中に含まれるのでx=2で最小となり、最小値は1となります。
[1]、[2]より、
0<a<2のときx=aで最小値=a2-4a+5、a≧2のときx=2で最小値=1・・・(答)となります。
(2)変域0≦x≦aの中央の値はa/2ですね。
[3]0<a/2<2つまり、0<a<4のとき、以下の図のように軸x=2は変域の中央よりも右側にあるのでx=0で最大となります。
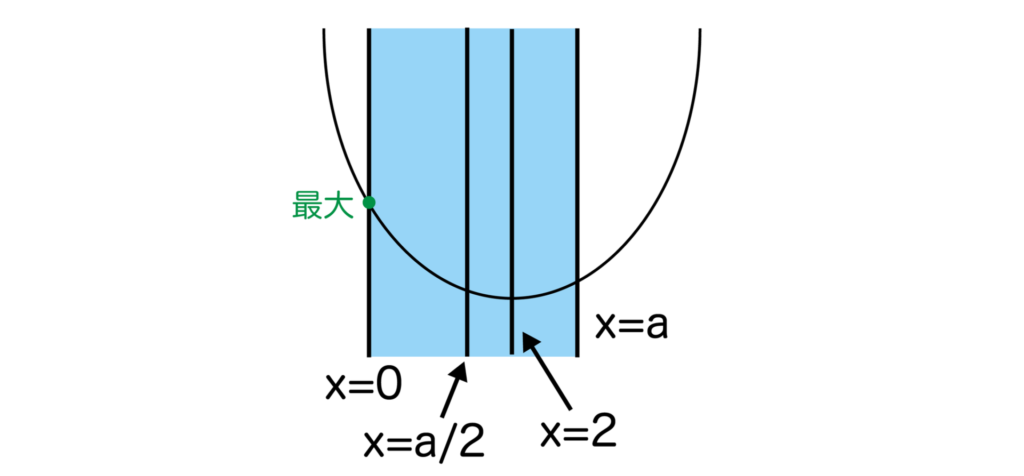
最大値=5となります。
[4]a/2=2、つまりa=4のときは以下の図のように軸x=2は区間の中央になるのでx=0、4で最大となります。
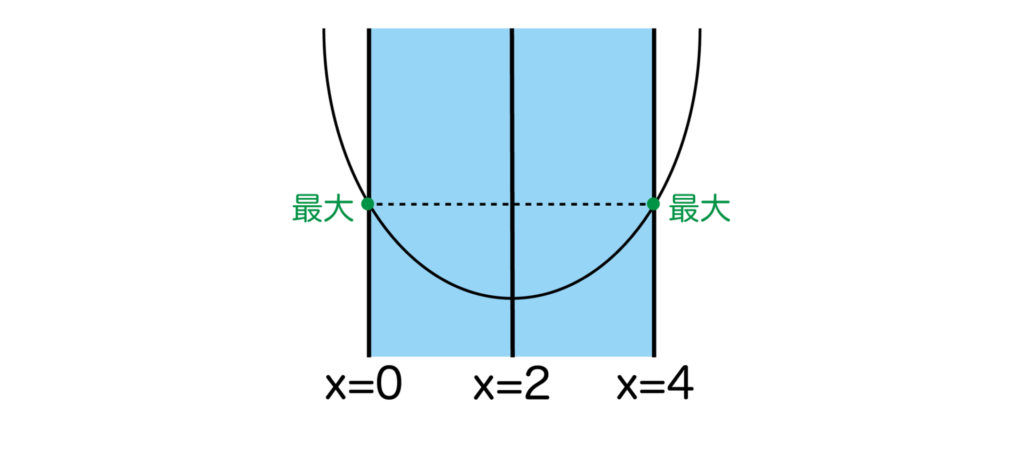
最大値はx=0を代入して、5となります。
[5]2<2/a、つまりa>4のときは以下の図のように軸x=2が区間の中央より左側にあるのでx=aで最大となります。
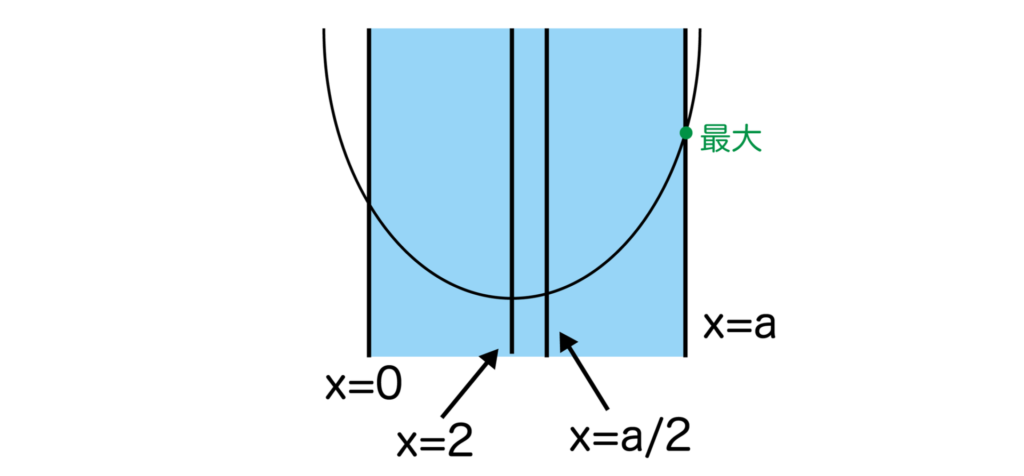
最大値はa2-4a+5となります。
以上[3]〜[5]より、
- 0<a<4のとき、x=0で最大値5
- a=4のとき、x=0、4で最大値5
- a>4のとき、x=aで最大値a2-4a+5
が答えとなります。
二次関数の最大値・最小値(式に文字があるver)
続いては、二次関数の式に文字があるバージョンの最大値・最小値に関する問題です。
【問題】
二次関数y=x2-2ax+a2-2a(0≦x≦2)の最小値が11になるような正の数aを求めよ。
【解答&解説】
x2-2ax+a2-2aを平方完成すると(x-a)2-2aとなりますね。
軸がx=aとなるので、場合分けを行います。
[1] 0<a≦2のとき、x=aで最小値は-2aとなりますね。
※aは正の数なのでa>0は確定です。
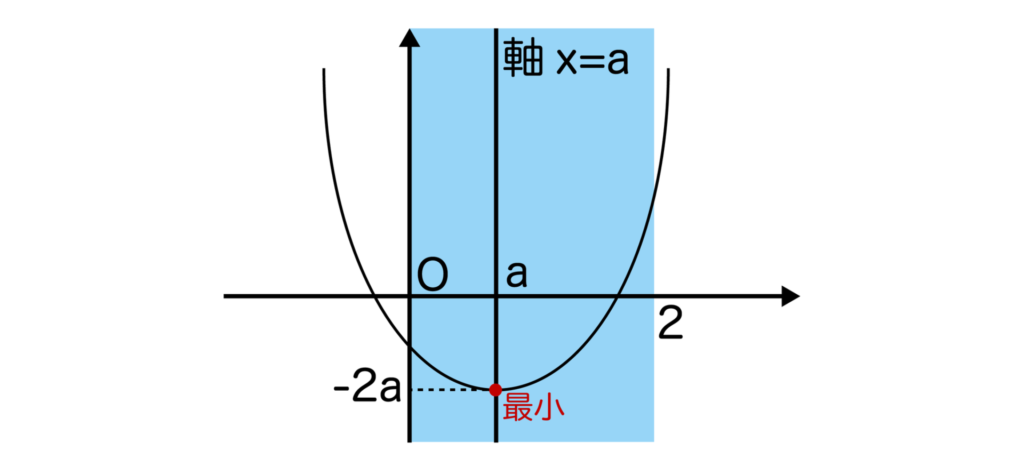
-2a=11より、a=-11/2となり、これは0<a≦2を満たさないので不適となります。
[2] 2<aのとき、x=2で最小値=22-2a×2-2a=a2-6a+4となりますね。
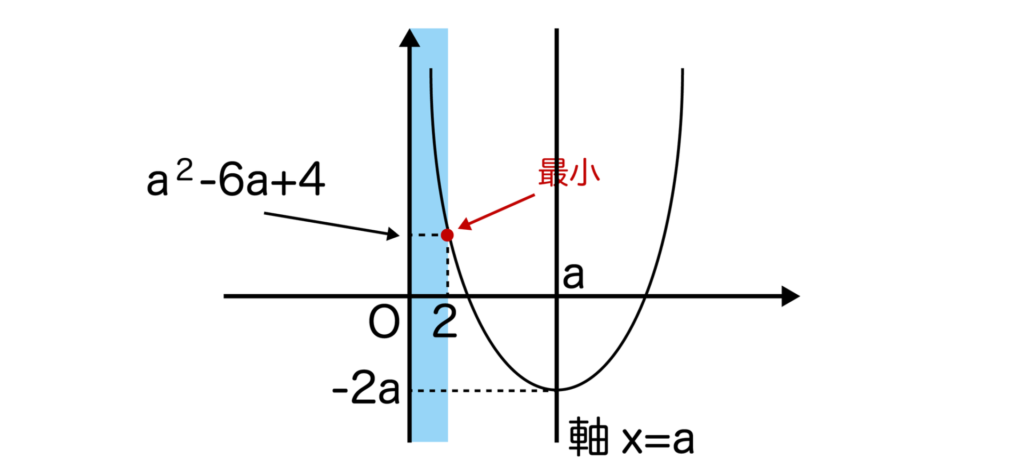
a2-6a+4=11より、(a+1)(a-7)=0となるのでa=-1、7となります。
※因数分解のやり方がわからない人は数学1の因数分解について解説した記事をご覧ください。
2<aを満たすのはa=7・・・(答)となります。
二次関数の最大値・最小値(式に文字が2つあるver)
今度は二次関数の式に文字が2つあるバージョンの問題です。
【問題】
y=ax2-2ax+b(0≦x≦3)の最大値が9、最小値が1のとき、aとbの値を求めよ。
【解答&解説】
ax2-2ax+bを平方完成すると、a(x-1)2-a+bです。
[1]a=0のとき、y=bとなり、これは条件を満たしません。
[2]a>0のとき、以下の図のように0≦x≦3の範囲ではx=3で最大値=3a+b、x=1で最小値=-a+bとなります。
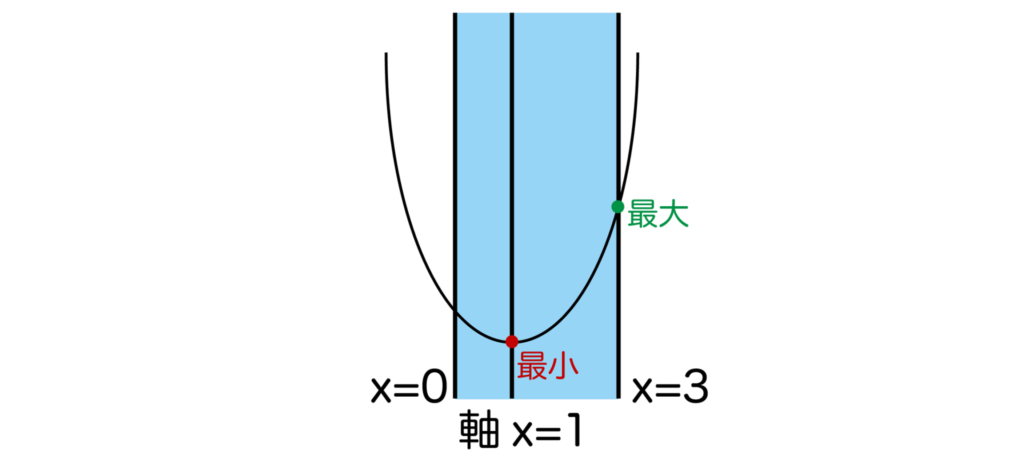
よって、3a+b=9、-a+b=1よりa=2、b=3となり、これはa>0を満たします。
[3]a<0のとき、以下の図のように0≦x≦3の範囲ではx=1で最大値=-a+b、x=3で最小値=3a+bとなります。
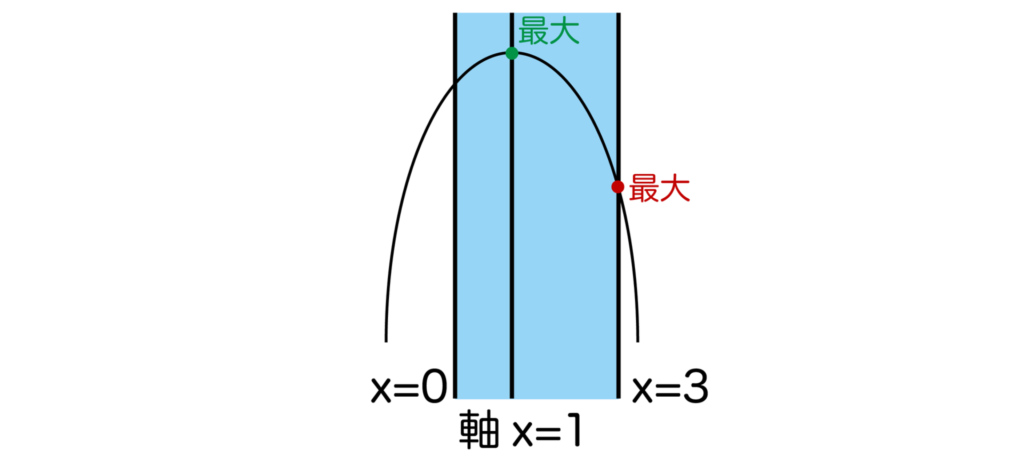
よって、-a+b=9、3a+b=1より、a=-2、b=7となり、これはa<0を満たします。
[1]〜[3]より、a=2、b=3またはa=-2、b=7・・・(答)となります。
二次関数の最大値・最小値を活用した文章題
最後は二次関数の最大値・最小値を活用した文章題です。
【問題】
直角を挟む2辺の長さの和が20である直角三角形において、斜辺の長さが最小の直角三角形を求め、その斜辺の長さを求めよ。
【解答&解説】
直角を挟む2辺のうち一方の辺の長さをxとします。すると、他方の辺の長さは20-xで表されますね。
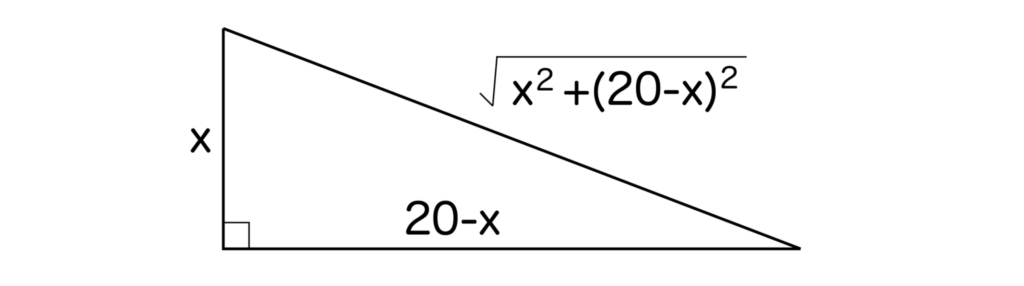
x>0、20-x>0より、0<x<20です。
斜辺の長さをaとすると、三平方の定理より
a2=x2+(20-x)2
=2x2-40x+400
=2(x-10)2+200
となるので、a2はx=10で最小値200となることがわかります。
このとき、他方の辺の長さは20-10=10となります。
よって斜辺の長さは√200=10√2・・・(答)となります。
※√(ルート)がわからない人は平方根とは何かについて解説した記事をご覧ください。
いかがでしたでしょうか?
今回は二次関数の最大値・最小値の基本事項と変域がある場合について解説していきました。
変域があるときは応用問題のような場合分けが必要なケースがあります。軸の位置をしっかりと意識しながら問題を解きましょう。


