高校数学の数学1では集合という分野を学習します。
集合や大学入試や共通テストでも頻出の分野の1つです。用語が多く登場するので、しっかりと理解しておきましょう。
本記事では、早稲田大学教育学部数学科を卒業した筆者が数学1で学習する集合で登場する記号や用語の意味・読み方、公式などをわかりやすく解説していきます。
最後には集合の練習問題も用意しています。
数学1の集合の意味とは?
まずは数学における集合の意味について解説します。
集合とは範囲がはっきりした数字の集まりのことです。
例えば「5以下の自然数からなる集合」は「自然数1、2、3、4、5」の集まりのことを言います。
「5以下の自然数」のように範囲が明確に定まっていることが重要です。
集合を構成している1つ1つ(上記の場合は1、2、3、4、5)のことを要素または元(げん)と言います。
aが集合Aの要素であるとき「aは集合Aに属する」と言い、a∈Aと表すことができます。
a∈Aの読み方は「aは集合Aに属する」で問題ありません。
また、「bが集合Aの要素でない」ことはb∉Aで表すことができます。
有限個の要素からなる集合は有限集合と呼ばれ、無限に多くの要素からなる集合は無限集合と呼ばれています。
先ほどご紹介した「5以下の自然数の集合」は要素が有限なので有限集合です。
一方で、例えば「5以上の自然数からなる集合」は要素が無限にあるので無限集合となります。
集合の表現方法
集合の表現方法は以下の2つがあります。
- 要素を1つ1つ記載する
- 要素の満たす条件を示す
例えば先ほどのご紹介した「5以下の自然数の集合」を表現することを考えてみましょう。この集合をAとします。
すると、Aには以下2つの表現方法があります。
A={1、2、3、4、5}
A={x | 1≦x≦5、xは自然数}
前者は1の表現方法で、後者は2の表現方法となります。
※「≦」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。
要素の個数が多い場合や無限集合の場合は「・・・」を用いて集合を表現することも可能です。
例えば、100以下の正の偶数の集合は{2、4、6、・・・98、100}のように表現することが可能です。
集合に関する用語
ここからは集合に関する用語を順番に解説していきます。
どれも重要な用語であり、用語の意味を理解しておかないと集合の問題が解けないので必ず理解するようにしておきましょう。
部分集合(A⊂B)
2つの集合A、Bにおいて、Aの全要素がBの要素となるとき、AはBの部分集合であるといい、 A⊂Bと表現します。
例えば、A={1、3、5}、B={1、2、3、4、5、6}であるとき、Aの全要素はBの要素となっています。
このとき「AはBに含まれる」または「BはAを含む」とも言います。
ちなみに、AとBの要素が完全に一致する場合はA=Bと表現します。
空集合(A=Ø)
空集合は「くうしゅうごう」と読みます。「からしゅうごう」ではないのでご注意ください。
空集合は要素を1個も持たない集合のことです。Øと表現されます。Øは「ファイ」と読みます。
例えば、A=Øと表現するとAは要素を1個も持たない集合ということになります。
共通部分(A∩B)
AとBどちらにも属する要素全体の集合のことをAとBの共通部分といい、A∩Bで表現します。
例えば、A={1、3、5、8、10}、B={1、2、3、4、5、6}であるとき、A∩B={1、3、5}となります。
集合の共通部分を考えるときは、以下のような図(ベン図と言います)を利用するとわかりやすいです。
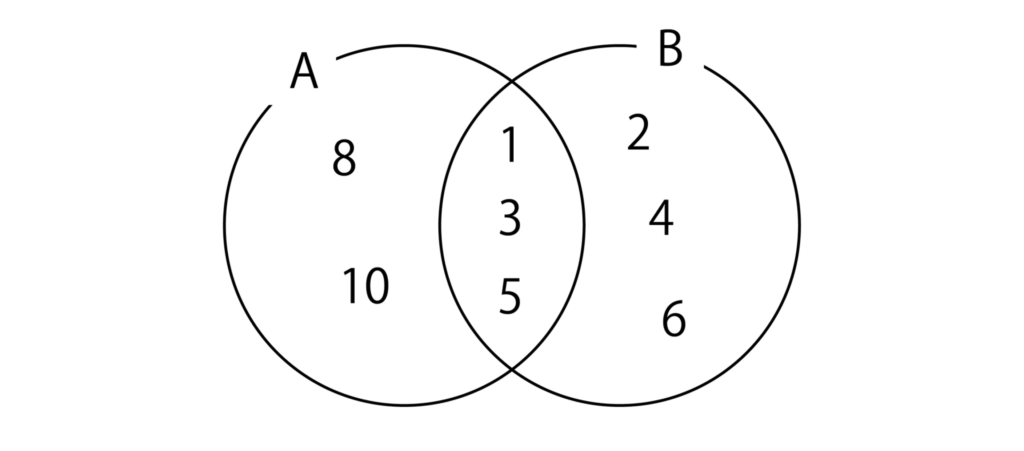
集合が3つある場合でも考え方は同じです。
例えば、A={1、2、3}、B={1、3、4、5}、C={1、3、5、6、7}であるとき、A∩B∩C={1、3}となります。
和集合(A∪B)
AとBの少なくとも一方に属する要素全体の集合のことをAとBの和集合といい、A∪Bで表現します。
例えば、先ほどと同様にA={1、3、5、8、10}、B={1、2、3、4、5、6}であるとき、A∪B={1、2、3、4、5、6、8、10}となります。
和集合を考えるときも、共通部分を同じようにベン図を利用するとわかりやすいです。

共通部分と同じく、集合が3つある場合でも考え方は同じです。
例えば、A={1、2、3}、B={1、3、4、5}、C={1、3、5、6、7}であるとき、A∪B∪C={1、2、3、4、5、6、7}となります。
全体集合と補集合
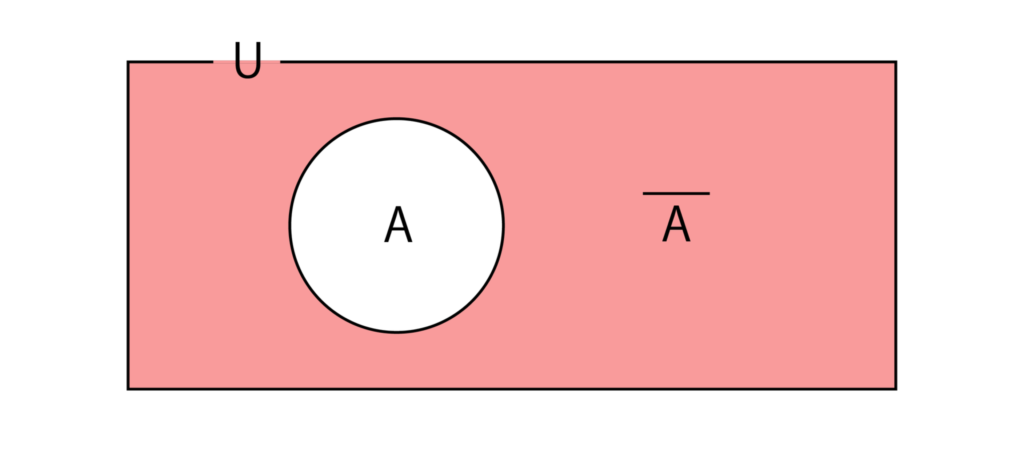
集合を考えるとき、1つの集合Uを最初に決め、Uの部分集合をAとしたとします。このとき、Uを全体集合といいます。
そして、全体集合Uの部分集合Aに対して、Aに属さないUの要素全体の集合をUに関するAの補集合といい、Aで表します。
ベン図で表現すると以下のようになります。
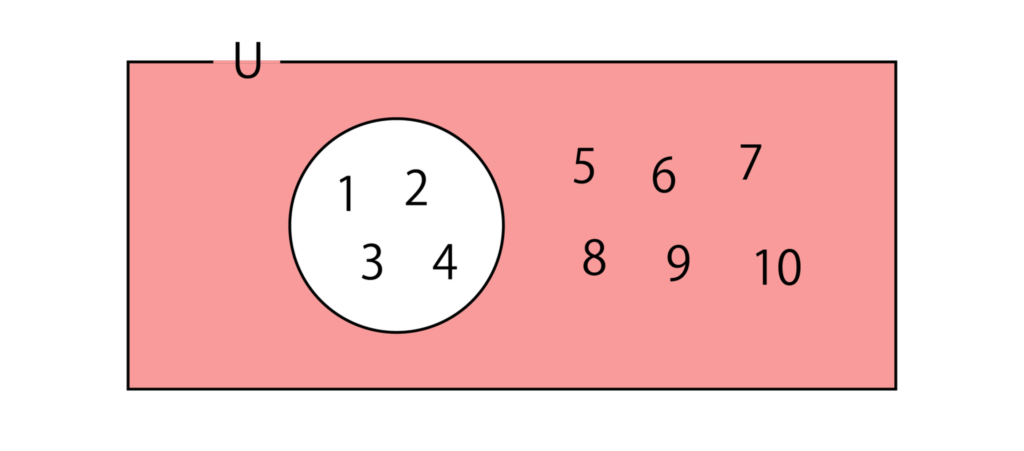
例えば、全体集合U={1、2、3、4、5、6、7、8、9、10}、Uの部分集合A={1、2、3、4}とします。
すると、A={5、6、7、8、9、10}となります。
ベン図で表現すると以下のようになります。
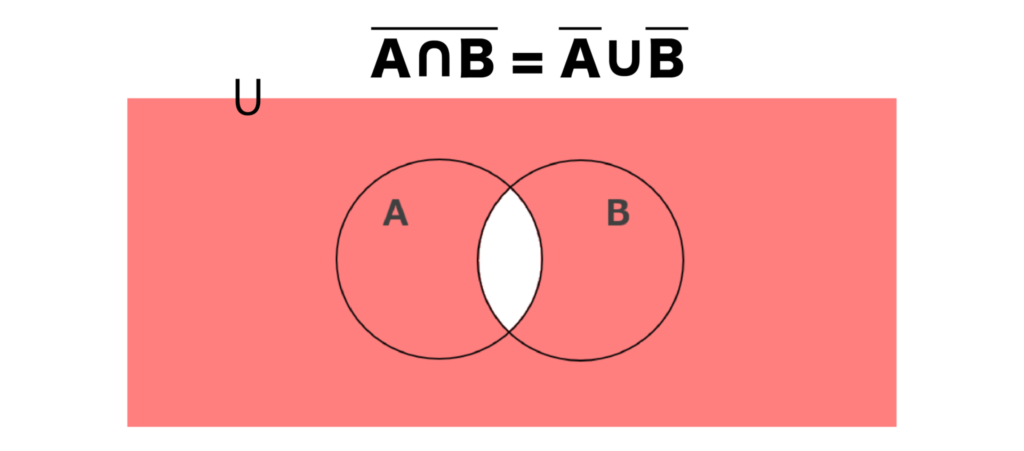
ド・モルガンの法則
集合でド・モルガンの法則は非常に有名なので、必ず覚えましょう。
ド・モルガンの法則は以下の通りです。
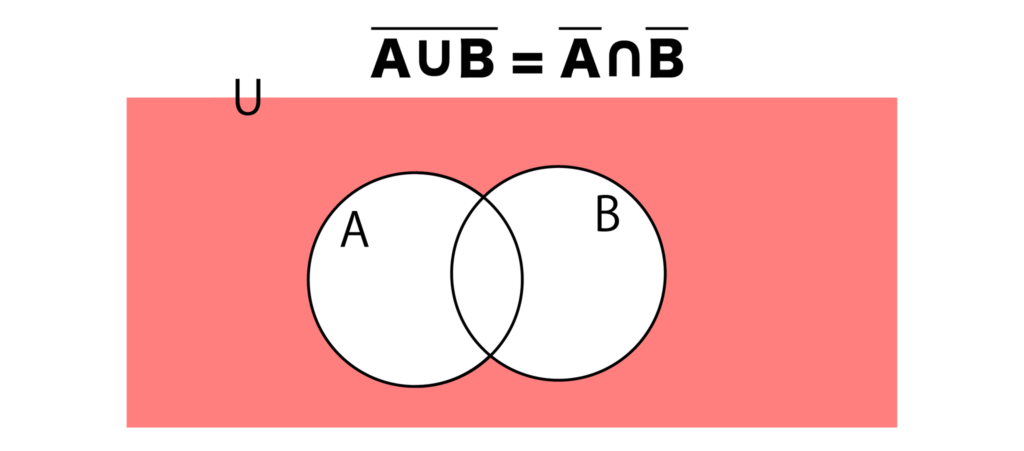
A∪B=A∩B
A∩B=A∪B
ド・モルガンの法則が成り立つことの証明はベン図を使うことで簡単にできます。
A∪B=A∩Bは以下のように証明できます。
A∩B=A∪Bは以下のように証明できます。
集合の練習問題
最後に集合の練習問題をご用意しました。
すべて基本的な問題なので、全問解けるまで繰り返し見返しましょう。
【練習問題1】
U={1、2、3、4・・・8、9}を全体集合とする。
集合Uの部分集合A、BをA={1、2、4、6、8}、B={1、3、6、9}としたとき、以下の集合を求めなさい。
(1)A∩B
(2)A∪B
(3)A∪B
(4)A∩B
【解答&解説】
(1)まずはU、A、Bをベン図で表現しましょう。以下のようになりますね。
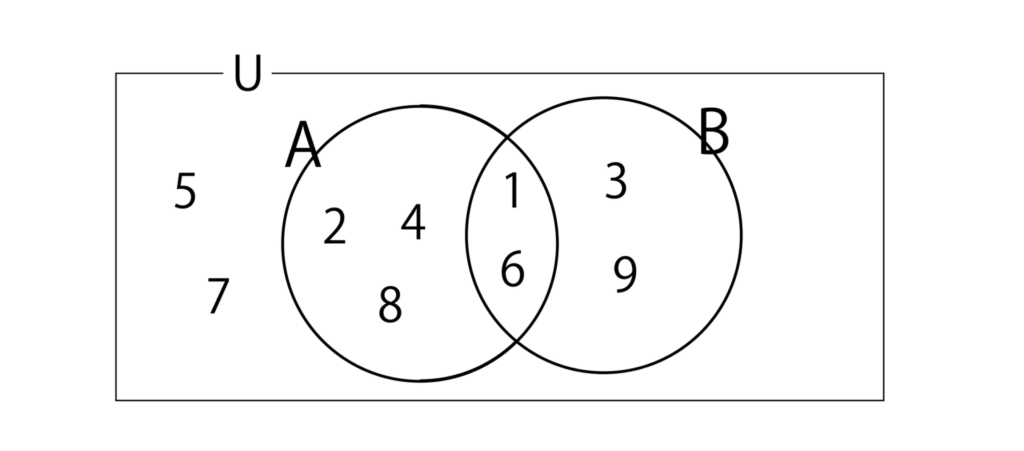
よって、A∩B={1、6}・・・(答)となります。
(2)A∪B={1、2、3、4、6、8、9}
(3)A∪B={2、3、4、5、7、8、9}
※先ほどご紹介したド・モルガンの法則です。
(4)A∩B={1、6}より、A∩B={2、3、4、5、7、8、9}・・・(答)となります。
【練習問題2】
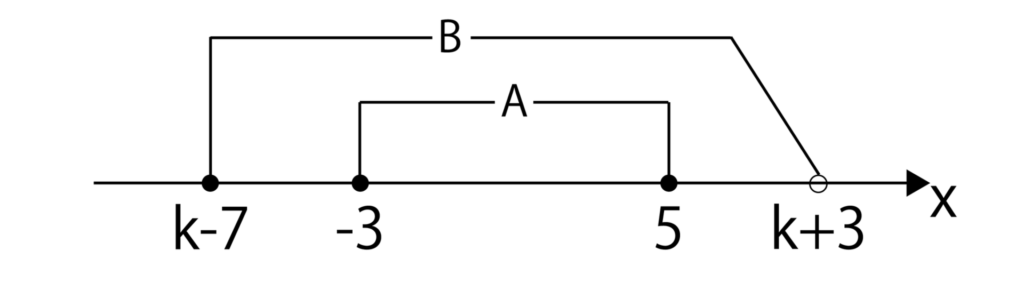
集合A、Bがあり、A={x | -3≦x≦5}、B={x | k-7≦x<k+3}とする。
※kは定数とする。
このとき、A⊂Bとなるkの値の範囲を求めなさい。
【解答&解説】
今回の練習問題はベン図ではなく、数直線を利用すると考えやすいです。
A⊂Bが成り立つとき、A、Bを数直線上に表すと以下のようになります。
※数直線上の●と◯の違いがわからない人は、一次不等式とは何かについて解説した記事をご覧ください。
よって、A⊂Bとなる条件はk-7≦-3、k+3>5が同時になる立つことです。
k-7≦-3=k≦4・・・①
k+3>5=k>2・・・②
より、①・②の共通範囲を求めて2<k≦4・・・(答)となります。
いかがでしたでしょうか?
今回は数学1における集合の記号や読み方、ド・モルガンの法則などについて解説したいきました。
繰り返しにはなりますが、集合は大学入試や共通テストでもよく出題されます。しっかりと勉強・対策をしておきましょう。


