正弦定理とは？公式と証明や外接円との関係など必須の知識を完全網羅

正弦定理とは何か・公式についてしっかりと理解できていますでしょうか？

正弦定理は大学入試や共通テストでも頻出なので、必ず公式を覚えておく必要があります。

本記事では早稲田大学教育学部数学科を卒業した筆者が正弦定理とは何か？正弦定理の公式や証明、外接円との関係、余弦定理との使い分けなど正弦定理に関して知りたい情報を完全網羅していきます。

最後には正弦定理に関する練習問題も用意しているので、ぜひ最後までお読みください。

正弦定理とは？公式をご紹介＆外接円とは？

まずは正弦定理の公式をご紹介します。

以下の図のように三角形ABCの外接円の半径をRとすると、a/sinA＝b/sinB＝c/sinC＝2Rが成り立つことを正弦定理と言います。

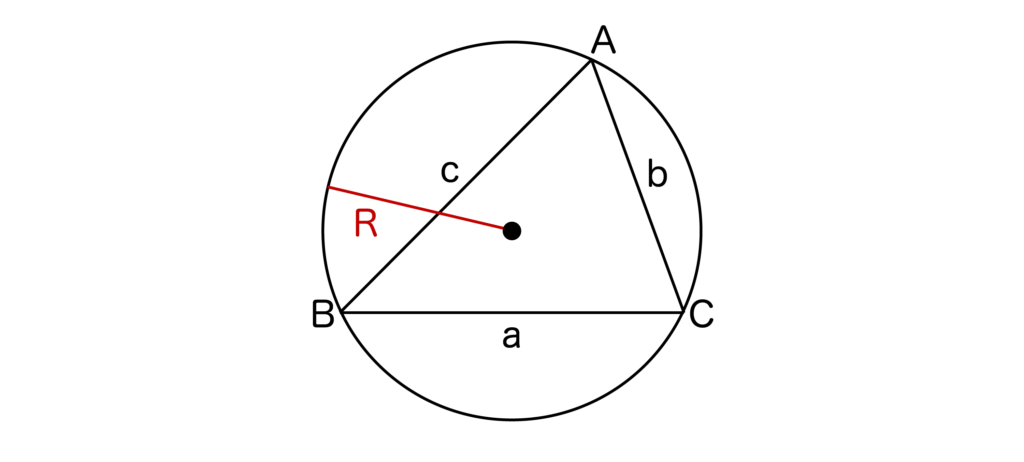
ここで外接円という言葉が登場しましたが、外接円とは三角形の3つの頂点を通る円のことです。

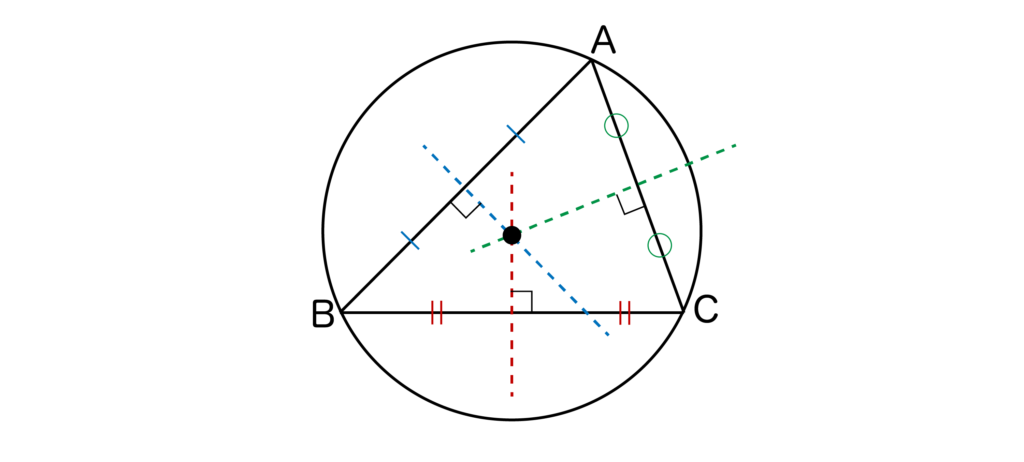
外接円の中心は各辺の垂直二等分線の交点となりますので、ぜひ覚えておきましょう。

正弦定理は大学入試や共通テストでも頻出です。三角関数では重要な公式がたくさん登場しますが、正弦定理も間違いなく重要な公式の1つなので、必ず暗記してください。

※外接円と似た用語として内接円があります。内接円とは何かについて解説した記事もご用意しているので、ぜひ合わせてご覧ください。

正弦定理の証明（成り立つ理由）

ここからは、正弦定理はなぜ成り立つのかの証明を行なっていきます。

【証明】

a=2RsinAは、半円の弧に対する円周角が90°であることを利用して、以下のように証明できます。

[1]A<90°のとき

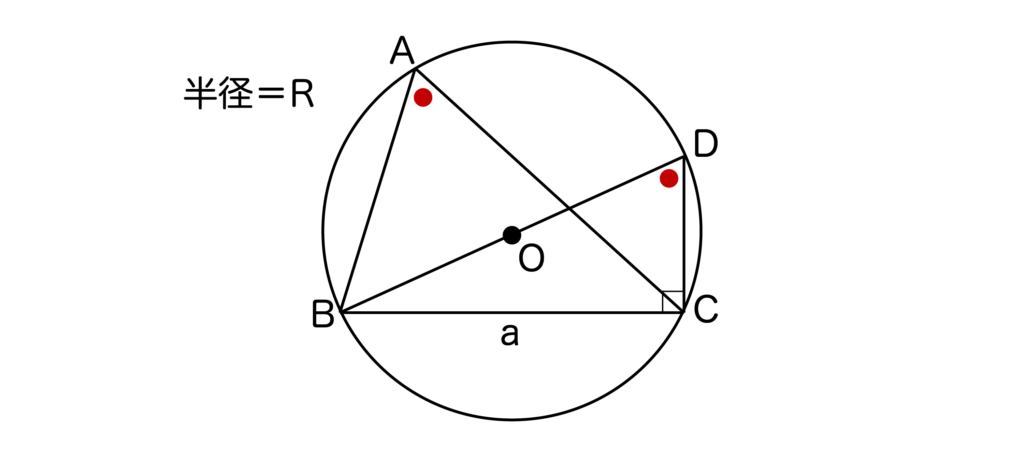
以下の図より、sinA=sinD=BC/BD=a/2Rとなります。

※sinの求め方がわからない人は三角比の覚え方について解説した記事をご覧ください。

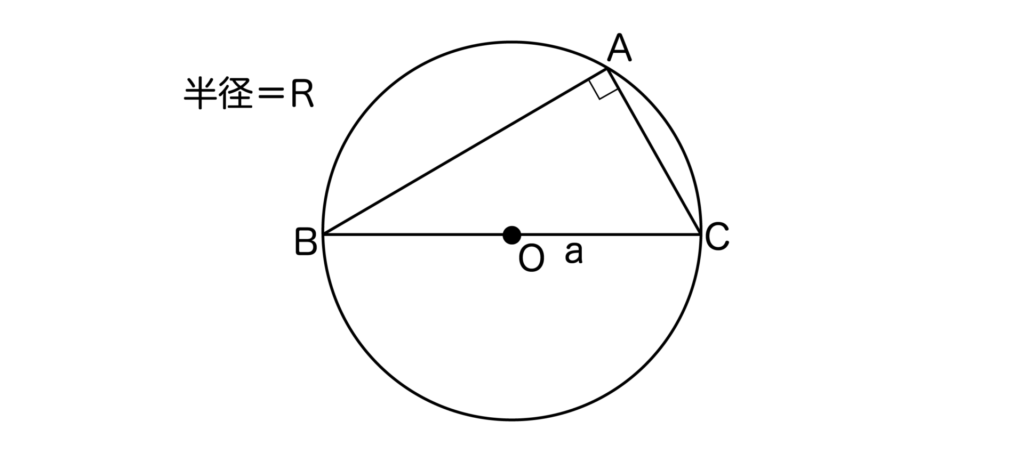
[2]A=90°のとき

以下の図より、2RsinA=2Rsin90°=2R=aとなります。

※sin90°＝1でした。詳しくはsin90度が1なのはなぜかについて解説した記事をご覧ください。

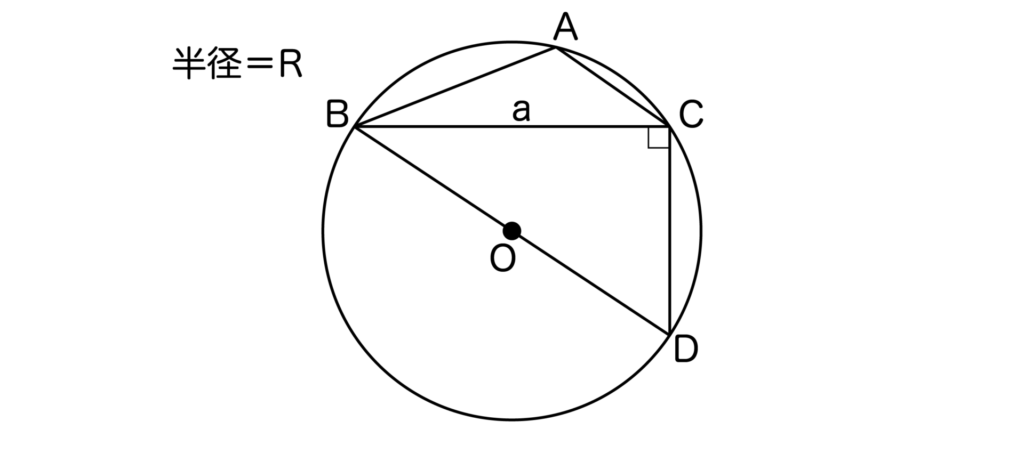
[3]A>90°のとき

以下の図より、sinA=sin（180°-D）=sinD=BC/BD=a/2Rとなります。

※円に内接する四角形の対角の和＝180°でした。したがって、∠BAC+∠BDC=180°となります。

同様に考えて、b=2RsinB、c=2RsinCが成り立ちます。

また、a=2RsinA、b=2RsinB、c=2RsinCからa：b：c＝sinA：sinB：sinCとなることがわかります。

以上より、正弦定理a/sinA＝b/sinB＝c/sinC＝2Rが証明できました。

正弦定理の覚え方

正弦定理a/sinA＝b/sinB＝c/sinC＝2Rの覚え方ですが、非常にシンプルな公式なので特に語呂合わせなどは必要ないかと思います。

正弦定理の公式を紙に書いて、その紙を家のトイレに貼っておきましょう。

そして、トイレに入るたびにその紙を見続けるのです。本記事の筆者は現役で早稲田大学教育学部数学科に合格していますが、どうしてもすぐに暗記したい公式などはこの方法で覚えていました。

割と複雑な公式であったとしても、トイレは毎日使うので1週間もあれば簡単に覚えてしまいます。

どうしても正弦定理が覚えられないという人にはおすすめの覚え方なので、ぜひ試してみてください。

正弦定理の例題

以上でご紹介した正弦定理の公式を踏まえて、例題を1つ解いてみましょう。

【例題】

三角形ABCにおいて、外接円の半径をRとする。b=4、B=30°、C=105°のとき、aとRの値を求めよ。

【解答＆解説】

まずは与えられた例題の問題文を図にしてみます。

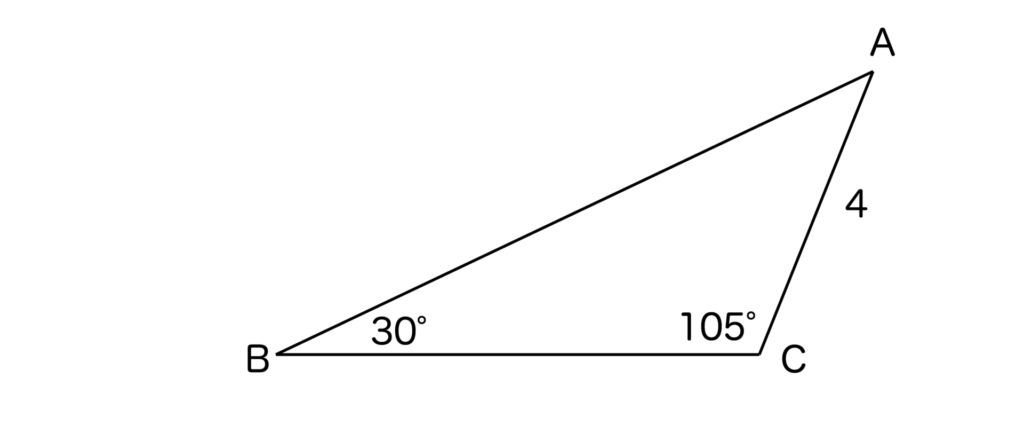
A＝180°-30°-105°＝45°ですね。

正弦定理よりa/sin45°＝4/sin30°となるので、

a=4/sin30° × sin45°＝4÷1/2 × 1/√2=4√2・・・（答）となります。

また、正弦定理より4/sin30°＝2Rなので、

R＝4/2sin30°＝4・・・（答）となります。

正弦定理と余弦定理の使い分け

正弦定理と一緒に学習する公式として余弦定理があります。

※余弦定理とは何かについて解説した記事もぜひ合わせてご覧ください。

正弦定理と余弦定理を学習しはじめたばかりの人は正弦定理と余弦定理の使い分けがわからないという人もいるのではないでしょうか？

というわけでここからは正弦定理と余弦定理の使い分けについて解説します。

1辺とその両端の角がわかっている場合＝正弦定理

例えば、以下のように1辺とその両端の角がわかっている場合は正弦定理を使います。例題をみてみましょう。

【例題】

以下の図において、ACの長さを求めなさい。

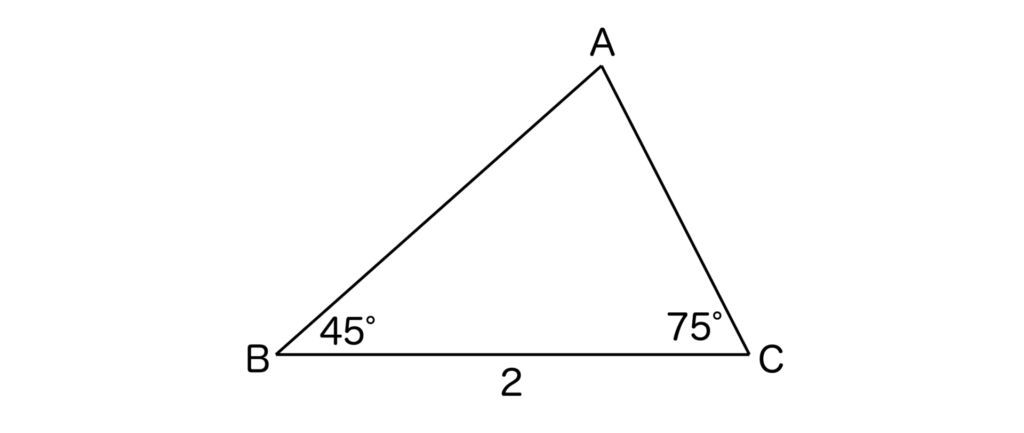
【解答＆解説】

∠A＝180°-45°-75°=60°であることがわかります。

正弦定理より、2/sin60°＝AC/sin45°が成り立ちますね。

sin60°＝√3/2、sin45°＝1/√2なので、AC＝2√6/3・・・（答）となります。

※sin60度の求め方について解説した記事やsin45度の求め方について解説した記事もご用意しているので、ぜひ参考にしてください。

2辺とその間の角がわかっている場合＝余弦定理

例えば、以下のように1辺とその両端の角がわかっている場合は余弦定理を使います。では、例題をみてみましょう。

【例題】

以下の図において∠Bの大きさを求めよ。

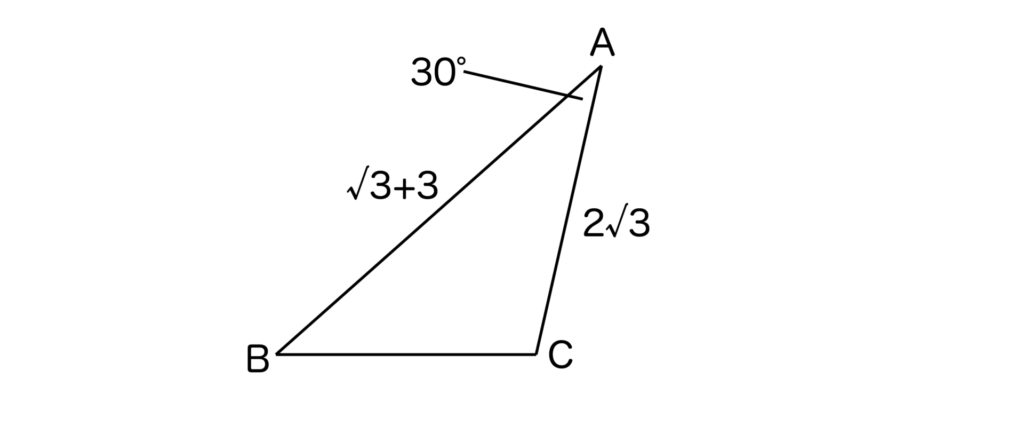
【解答＆解説】

まずは∠Aの大きさがわかっているので、∠Aに注目しましょう。

余弦定理より、BC²=AB²+AC²-2・AB・BC・cos30°が成り立つので、

BC²＝（12＋6√3）＋12-（12+12√3）・√3/2より、BC²＝6となります。

※cos30°＝√3/2です。詳しくはsin30度の求め方について解説した記事をご覧ください。

したがって、BC＝√6となります。

ここで、再び余弦定理を使います。

cosB

＝（AB²+BC²-AC²）/2・AB・BC

＝（√3+3）²+（√6）²-（2√3）²/2（√3+3）（√6）

＝1/√2となります。

よって、B=45°となります。

3辺がわかっている場合＝余弦定理

最後は3辺がわかっている場合です。この場合も余弦定理を使います。

では、例題を解いてみましょう。

【例題】

以下の図において∠Aの大きさを求めよ。

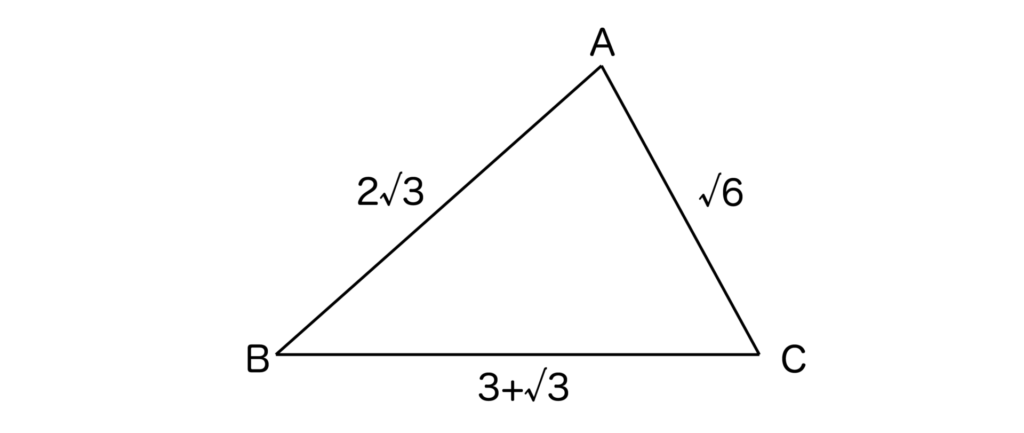
【解答＆解説】

BC=a、AC=b、AB=cとします。

余弦定理より、

cosA

＝（b²+c²-a²）/2bc

＝（√6）²+（2√3）²-（3+√3）²/2・√6・2√3

＝√3/2

となるので、A=30°となります。

正弦定理と余弦定理の使い分けに関しては、1辺とその両端の角がわかっている場合のみ正弦定理が使えると思っておきましょう。

正弦定理の練習問題

正弦定理の練習問題を解いてみましょう。正弦定理に限らずですが、たくさんの問題を解くことで公式は自然と頭に入ってきますよ。

【練習問題】

三角形ABC において、a＝√6、b＝2、A＝60°のとき、BとCの角の大きさを求めよ。

【解答＆解説】

与えられた問題文を図にすると以下のようになりますね。

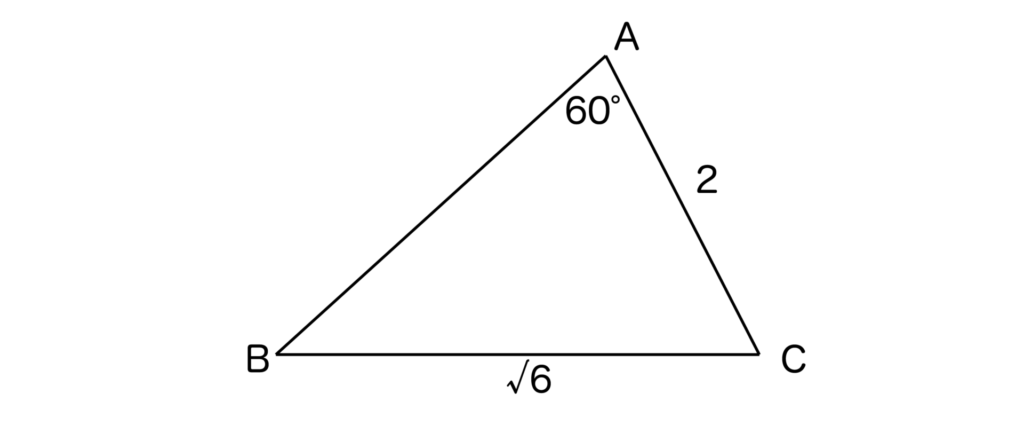
正弦定理より、√6/sin60°＝2/sinBとなるので、

sinB=2/√6・sin60°=2/√6・√3/2＝1/√2よりB=45°・・・（答）となります。

よって∠C＝180°-60°-45°＝75°・・・（答）となります。

【最後に】正弦定理と逆数

上記の練習問題で√6/sin60°＝2/sinBからsinB=2/√6・sin60°としていますが、この変形がわからない人が多いのでこの部分だけ丁寧に解説しておきます。

まず、√6/sin60°＝2/sinBにおいて両辺にsinBをかけます。すると、

√6/sin60° × sinB＝2となりますね。

その後、両辺を√6/sin60°で割ります。すると、

sinB＝（2 × sin60°）/√6＝2/√6 × sin60°となりますね。

√6/sin60°で割るということは√6/sin60°の逆数であるsin60°/√6をかけるということなので、その点に注意しましょう。

今回は正弦定理の公式や証明、正弦定理と余弦定理の使い分けなどについて解説していきました。

繰り返しにはなりますが、正弦定理は大学入試・共通テストともに頻出の公式です。必ずマスターしておきましょう。