内角や外角については中学数学でも学習する内容です。
しかし、高校数学の数学Aでも教科書によっては中学数学の復習として簡単に取り上げているものもあります。
なので、本記事でも数学Aの内容の1つとして内角・外角を念の為取り上げておきます。
内角・外角は図形問題を解く上で必須の知識なので、必ず理解しておきましょう。
今回は早稲田大学教育学部数学科を卒業した筆者が内角・外角とは何かだけでなく、内角の和や外角の和、求め方や公式を図解でわかりやすく解説していきます。
内角・外角とは?
内角とはその名の通り「内側にある角」のことです。
例えば、三角形の場合は3つの内角があります。
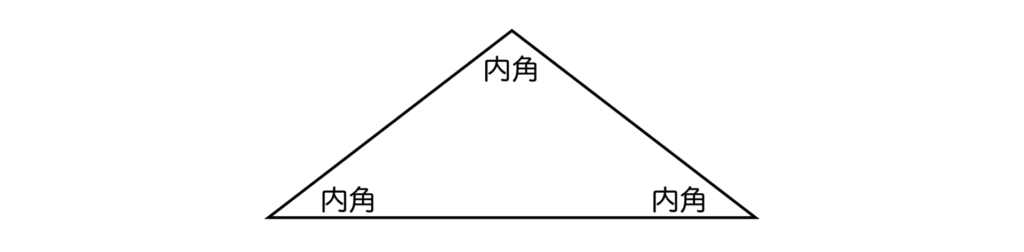
四角形であれば4つの内角があります。

六角形であれば6つの内角があります。
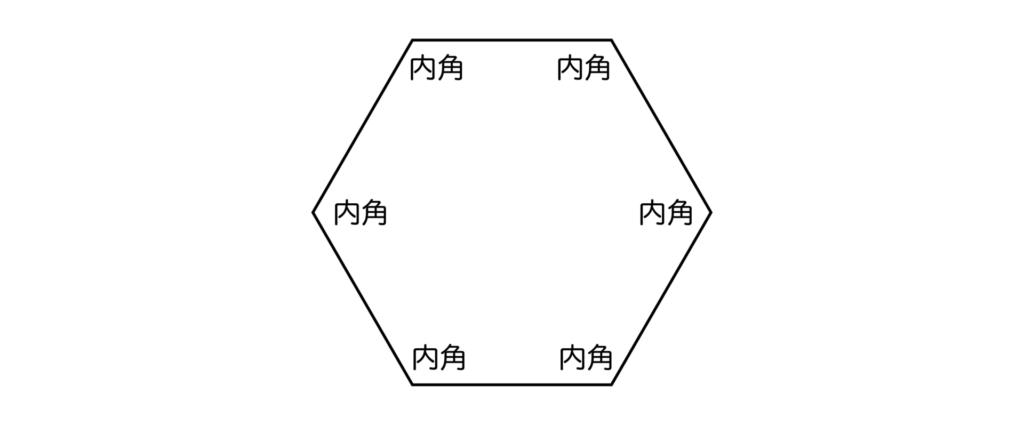
つまり、n角形であればn個の内角が存在するということです。
それに対して外角とはその名の通り「外側にある角」のことです。外角は辺を延長することによって作られる角です。
例えば、三角形の外角は以下のように3つあります。
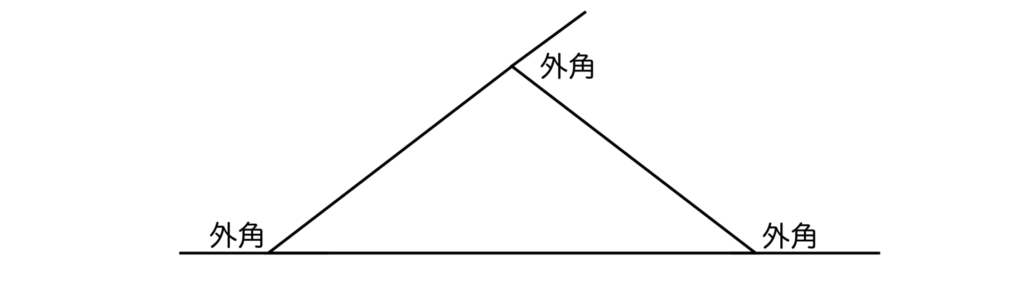
外角=辺を延長することによって作られるならば、例えば以下の三角形ABCにおいて、角Bの外角は2つあるのでは?と思う人がいるかもしれません。
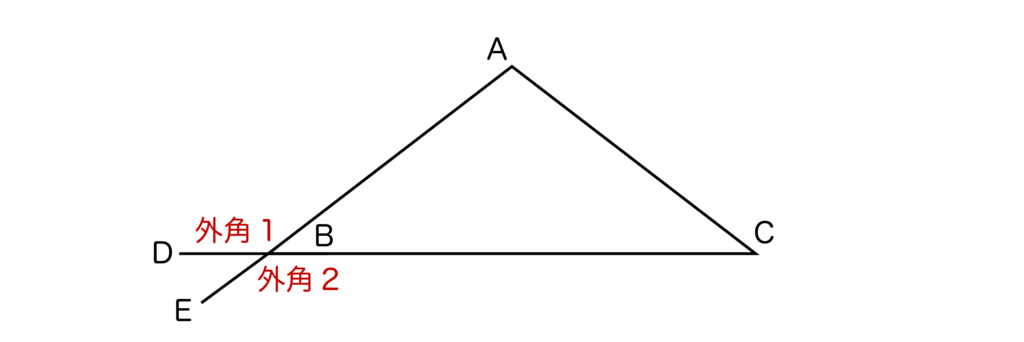
これは確かにその通りですが、外角1の大きさ=外角2の大きさなので、外角1と外角2は同じものとみなします。なので、三角形における外角は3つとなります。
では、次は四角形の外角を考えてみましょう。四角形の外角は以下のように4つとなります。

次は六角形の外角です。六角形の外角は以下のように6つとなります。
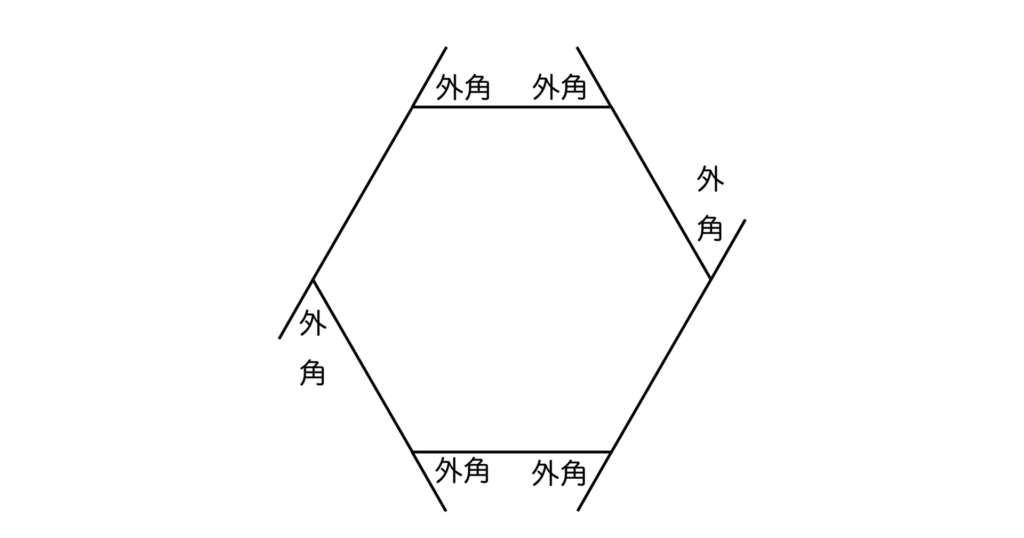
内角のときと同様に、n角形であればn個の外角が存在します。
三角形の内角の和と証明
三角形の内角の和は180°です。これは必ず暗記しておきましょう。
三角形の内角の和が180°になる理由は以下のように証明できます。
【証明】
以下の三角形ABCにおいて、BCをCの方向に延長させ、点Dを設定します。
また、点Cを通り、ABと並行な直線を引き、以下のように点Eを設定します。
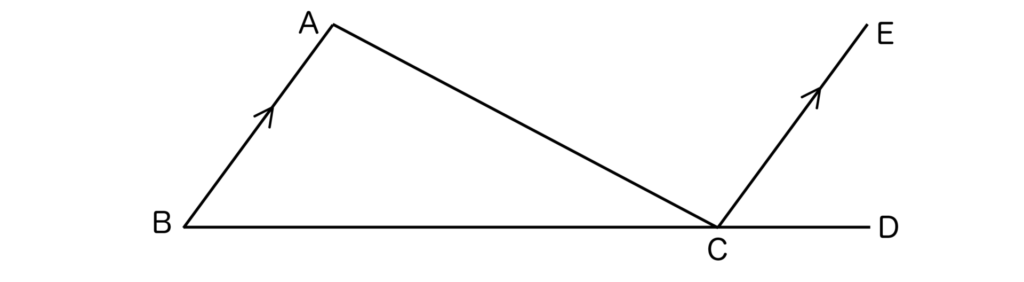
すると、同意角は等しいので∠ECD=∠ABCとなりますね。
また、錯角は等しいので∠ECA=∠BACとなります。
※同意角や錯覚がわからない人は対頂角・同位角・錯角とは何かについて解説した記事をご覧ください。
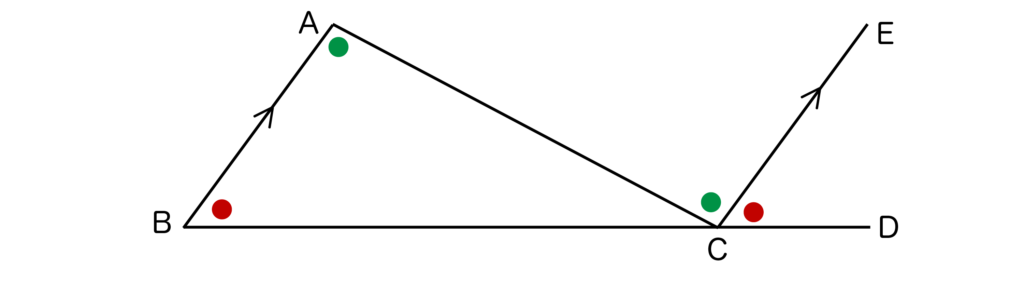
ここで、∠ACB+∠ACE+∠ECDは一直線になっていることがわかります。
つまり、∠ACB+∠ECA+∠ECD=180°です。
上記の通り、∠ECA=∠BAC、∠ECD=∠ABCなので、
∠ACB+∠BAC+∠ABC
=∠ACB+∠ECA+∠ECD
=180°となります。
以上で三角形の内角の和が180°であることが証明できました。
数学の問題を解くにあたって、三角形の内角の和が180°であることは証明なしに使って問題ありません。
多角形の内角の和と証明
では、三角形以外の図形の内角の和はどうなるでしょうか?
まずは四角形から考えてみましょう。以下のような四角形ABCDがあったとき、BCを結んで四角形ABCDを三角形ABCと三角形BCDに2分割します。
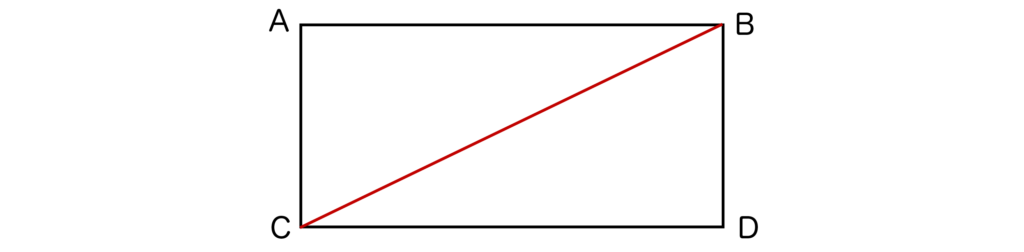
先ほど解説した通り、三角形の内角の和は180°です。
よって、四角形ABCの内角の和
=三角形ABCの内角の和+三角形BCDの内角の和
=180°+180°
=360°
となります。
では、六角形の内角の和はどうなるでしょうか?
以下のように六角形ABCDEFを考えてみます。AC、AD、AEを結ぶと三角形が4つできることがわかりますね。
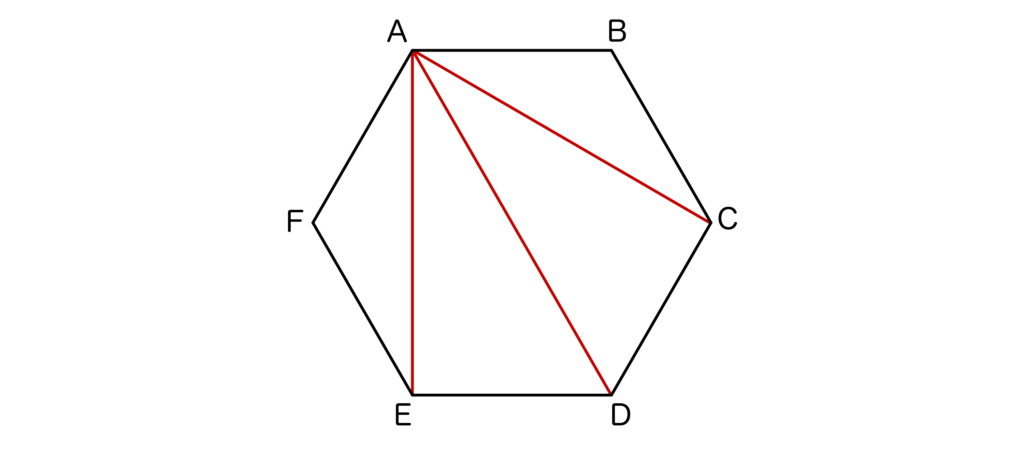
よって六角形の内角の和=180°×4=720°となります。
※六角形の内角の和について詳しく解説した記事もぜひ合わせてご覧ください。
以上より、四角形=三角形が2つ、六角形=三角形が4つできることがわかりました。
一般的に、n角形においては(n-2)個の三角形ができます。
よって、n角形の内角の和=(n-2)×180°=180°×n-360°で表すことができます。
これも公式の1つとして覚えておきましょう。
三角形の外角の和と証明
ここからは外角について解説していきます。以下で詳しく解説しますが、外角の和はどんな多角形でも必ず360°になります。
まずは三角形の外角の和=360°になる理由(証明)から解説していきます。
【証明】
以下の三角形ABCにおいて、同意角と錯角は等しいことから、
∠ECD=∠ABC、∠ECA=∠BAC
が成り立つのでした。

ここで、∠ACB(=∠C)の外角=∠ACDですね。
そして、図より∠ACD=∠ECD+∠ECAであることがわかります。
ここで、∠ECD=∠ABC、∠ECA=∠BACなので、
∠ACB(=∠C)の外角=∠ABC+∠BACとなることがわかります。
つまり、外角の大きさは他の2つの内角の和となるのです。
同様に考えて、
∠Bの外角=∠BAC+∠BCA、∠Aの外角=∠ABC+∠BCAとなります。
以上より、∠A・∠B・∠Cの外角の和
=(∠ABC+∠BAC)+(∠BAC+∠BCA)+(∠ABC+∠BCA)
=2×(∠ABC+∠BAC+∠BCA)
となります。ここで、三角形の内角の和=180°であることから、∠ABC+∠BAC+∠BCA=180°です。
したがって、∠A・∠B・∠Cの外角の和=2×180°=360°となります。
多角形の外角の和と証明
上記でも解説した通り、外角の和は内角の和と違ってどんな多角形でも常に360°となります。
その理由ですが、上記でも解説した通り、n角形の内角の和は(n-2)×180°で求められるのでした。
ここで、n角形の1つの内角と外角は合わせて180°であることに注目します。
すると、(n角形の内角の和)+(n角形の外角の和)=n×180°になりますね。
よって、(n角形の外角の和)
=n×180°-(n角形の内角の和)
=n×180°-{(n-2)×180°}
=360°
となるので、多角形の外角の和は常に360°となることが証明できます。
内角と外角の性質まとめ
以上で内角と外角の性質を解説していきました。
今一度、上記で解説したことをまとめておきます。
- 三角形の内角の和は180°である
- n角形の内角の和は(n-2)×180°=180°×n-360°である
- 三角形の1つの外角は、それと隣り合わない2つの内角の和に等しい(以下の図参照)
- 外角の和はどんな多角形においても常に360°である

内角と外角に関する練習問題
最後に、上記で学習した内角と外角の性質を踏まえて、練習問題を解いてみましょう。
すべて基本的な問題なので、全問正解できるまで内角と外角の性質を理解してください。
【練習問題】
(1)以下の三角形ABCにおいて、∠A=92°、∠B=30°である。このとき、∠Cの外角の大きさを求めよ。
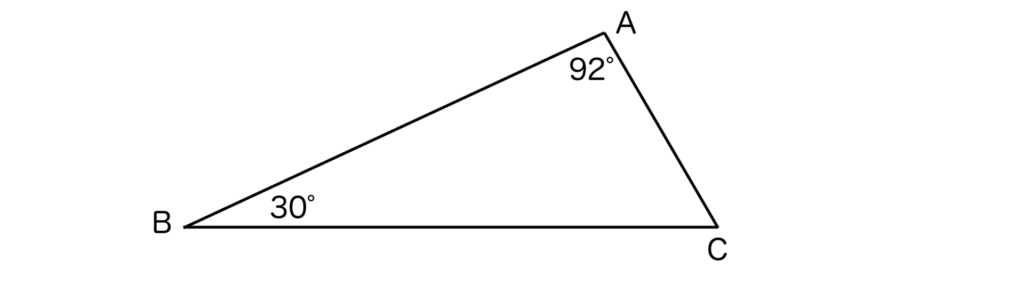
(2)正二十角形の1つの内角の大きさを求めよ。
【解答&解説】
(1)∠Cの外角の大きさ=∠A+∠B=92°+30°=122°・・・(答)となります。
【検算】三角形の内角の和=180°でした。よって、∠C=180°-92°-30°=58°です。
∠Cの外角の大きさ=180°-58°となるので、確かに122°となっていることが確認できます。
(2)n角形の内角の和は(n-2)×180°でした。
よって、正二十角形の内角の和=(20-2)×180°=3240°となります。
正二十角形なので、内角は20個あり、すべての内角は同じ大きさです。
よって、1つの内角の大きさ=3240°÷20=162°・・・(答)となります。
いかがでしたか?
今回は内角・外角とは何かについて解説した後、内角の和や外角の和について解説していきました。
内角・外角の性質は数学の図形問題を解く上では必須の知識なので、必ず理解しておきましょう。


