内接円とは何かについて皆様は解説できますでしょうか?
後ほど詳しく解説しますが、内接円とは三角形のそれぞれの角の二等分線の交点を中心とした円のことです。
本記事では早稲田大学教育学部数学科を卒業した筆者が内接円とは何かについて解説した後、内接円の半径の求め方や内接円を利用した三角形の面積の求め方など、内接円に関して必ず知っておくべき情報を一挙に解説していきます。
ぜひ最後まで本記事をお読みいただき、内接円をマスターしてください。
内接円とは?内心とは?
まずは内接円とは何かについて解説します。
内接円とは以下のように三角形ABCにおいて、それぞれの角の二等分線の交点を中心とした円のことです。
三角形ABCの3つの頂点は内接円の円周上に存在します。
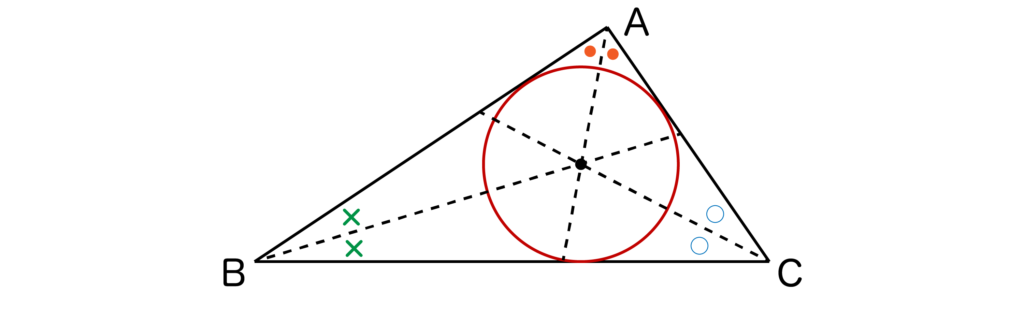
また、内接円の中心は内心と呼ばれていますので、ぜひ覚えておきましょう。
ちなみにですが、内接円と似たような用語として外接円があります。
外接円は以下のように三角形の3つの頂点を通る円のことです。外接円の中心は各辺の垂直二等分線の交点になります。
※詳しくは正弦定理とは何かについて解説した記事をご覧ください。
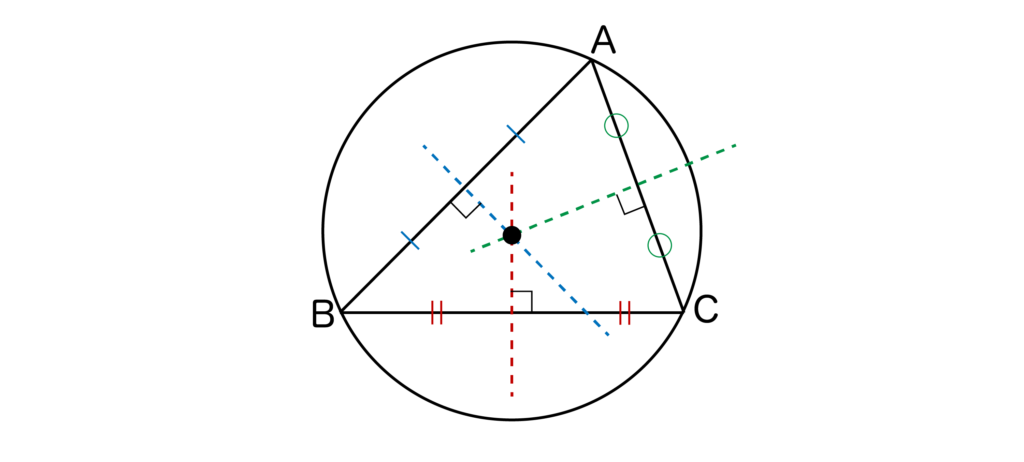
内接円と外接円はぜひセットで覚えておきましょう。
内接円の証明
ここからは、△ABCの∠Bと∠Cの二等分線の交点をDとするとADはなぜ∠Aを二等分するのかについて証明していきます。
【証明】
以下のように、内接円の中心DからAB、BC、CAのそれぞれに垂線を下ろします。
そして、それぞれの辺と垂線との交点を以下のようにP、Q、Rとします。
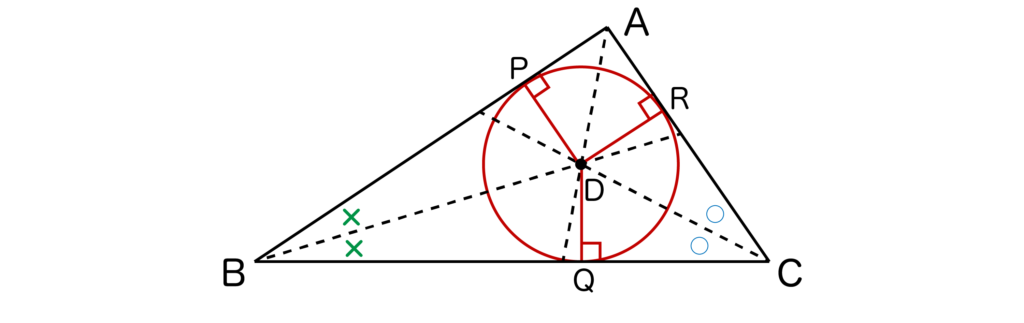
そして、三角形PBDと三角形QBDに注目すると、
- BD共通・・・①
- ∠PBD=∠QBD・・・②
- ∠BPD=∠BQD=90°・・・③
ですね。
よって、①・②・③より斜辺と1つの鋭角がそれぞれ等しい(直角三角形の合同条件)ので、三角形PBD≡三角形QBDとなります。
※三角形と直角三角形の合同条件について解説した記事もぜひご覧ください。
したがって、PD=QD・・・④となります。
同様に考えて、三角形QCD≡三角形RCDよりQD=RD・・・⑤が導けます。
④・⑤よりPD=RDとなります。
三角形PADと三角形RADにおいて斜辺と他の1辺がそれぞれ等しい(直角三角形の合同条件)ことから、三角形PAD≡三角形RADとなるので、∠PAD=∠RADとなります。
【証明終】
直角三角形の合同条件という懐かしい用語が登場しましたが、証明方法としてはシンプルかと思いますので、できるようにしておきましょう。
内接円の半径の求め方と証明
ここからは内接円の半径の求め方について解説していきます。
以下の図のように三角形ABCの面積=Sとすると、内接円の半径r=2S/(a+b+c)となります。
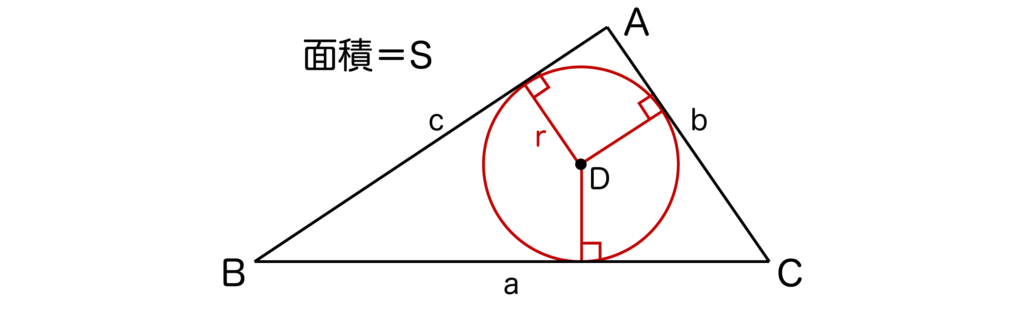
では、なぜ内接円の半径r=2S/(a+b+c)となるのでしょうか?
ここからは証明を行なっていきます。
【証明】
以下の図のように内接円の中心である点Dから三角形ABCの各頂点に線を引きます。
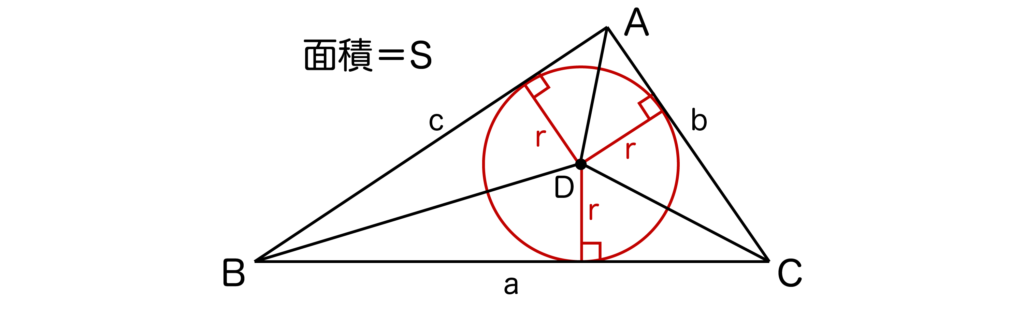
すると、
- 三角形DBCの面積=ar/2
- 三角形DACの面積=br/2
- 三角形DABの面積=cr/2
となりますね。
よって、三角形ABCの面積S=(ar+br+cr)/2より、
2S=r(a+b+c)となるので、r=2S/(a+b+c)を導くことができます。
【証明終】
証明方法としては簡単だったかと思います。
内接円の半径r=2S/(a+b+c)は大学入試や共通テストでも頻出なので、必ず覚えておきましょう。
内接円から面積を求める方法
先ほど解説した通り、内接円の半径r=2S/(a+b+c)なので、三角形ABCの面積S=r(a+b+c)/2で求めることができます。

- 内接円の半径を求める場合はr=2S/(a+b+c)
- 三角形の面積を求める場合はS=r(a+b+c)/2
となります。どちらも使えるようにしておきましょう。
内接円の半径と三角形の面積を求める練習問題
最後に、内接円の半径と三角形の面積を求める練習問題をご用意しました。
以上で学習した公式をもとにぜひ解いてみてください。
【練習問題1】
以下の三角形ABCにおいて、内接円の半径と三角形ABCの面積を求めよ。
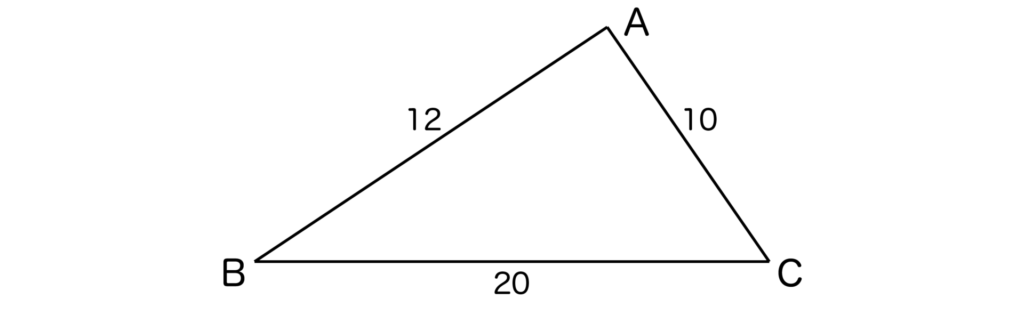
【解答&解説】
まずは三角形の面積から求めましょう。
ヘロンの公式より、2s=20+10+12とすると、2s=42よりs=21となります。
※ヘロンの公式がわからない人は三角形の面積の求め方の公式3つをご紹介した記事をご覧ください。
したがって、三角形ABCの面積=√21(21-20)(21-10)(21-12)=√21・1・11・9=3√231・・・(答)となります。
内接円の半径をrとすると、r=2S/(a+b+c)=2・3√231/ (20+10+12)=√231/7・・・(答)となります。
【練習問題2】
以下の三角形ABCにおいて、内接円の半径と三角形ABCの面積を求めよ。
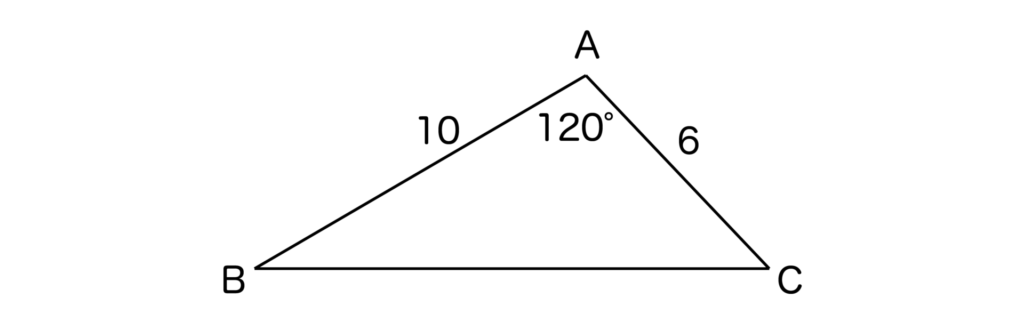
【解答&解説】
今回は3辺ではなく、2辺のその間の角がわかっていますね。
三角形ABCの面積は1/2・AB・AC・sinAで求められるのでした。
よって、1/2・10・6・sin120°=1/2・10・6・√3/2=15√3・・・(答)となります。
※sin120°が√3/2になる理由がわからない人はsin120度の求め方について解説した記事を参考にしてください。
ここで、内接円の半径=2・15√3/(a+b+c)ですが、まだaがわかっていない状態なのでa(=BC)を求めましょう。
余弦定理より
cosA=(62+102-BC2)/2・6・10ですね。
※余弦定理がわからない人は余弦定理とは何かについて解説した記事をご覧ください。
cosA=cos120°=-1/2なので、
-1/2=(62+102-BC2)/2・6・10より、
-1/2=(136-BC2) / 120となるので、
BC2=196となりますね。BC>0なので、BC=14が求まります。
したがって、内接円の半径=2・15√3/ (14+10+6)=√3・・・(答)となります。
いかがでしたでしょうか?
今回は内接円とは何かについて解説した後、内接円の半径や三角形の面積の求め方について解説しました。
繰り返しにはなりますが、内接円の公式は大学入試や共通テストでも頻出です。外接円とセットで必ず覚えておきましょう。


