二次不等式の解き方を簡単に解説！公式＋判別式の使い分け・見分け方も！練習問題付き

二次不等式の解き方は理解できていますでしょうか？

二次不等式では判別式が登場するケースもあるので、いつ判別式を使えばいいのか見分けがつかないという人も多いのではないでしょうか？

そこで今回は早稲田大学教育学部数学科を卒業した筆者が二次不等式の解き方・公式を簡単に解説していきます。

また、判別式の使い分け・見分け方についても解説していきます。

二次不等式の解き方・公式

二次不等式の解き方ですが、まずは公式をしっかりと理解する必要があります。

a>0かつ判別式D>0のとき、二次方程式ax²+bx+c=0の異なる2つの解をα、β（α<β）とします。

※判別式がわからない人は判別式とは何かについて解説した記事をご覧ください。

このとき、

• ax²+bx+c>0の解は、x<α、β<x
• ax²+bx+c<0の解は、α<x<β
• ax²+bx+c≧0の解は、x≦α、β≦x
• ax²+bx+c≦0の解は、α≦x≦β

となります。

※記号「>」「<」や「≧」「≦」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。

また、

• （x-α）（x-β）>0の解は、x<α、β<x
• （x-α）（x-β）<0の解は、α<x<β
• （x-α）（x-β）≧0の解は、x≦α、β≦x
• （x-α）（x-β）≦0の解は、α≦x≦β

となります。

さらに、a>0かつ判別式D=0のとき、二次方程式ax²+bx+c=0の重解をαとします。

※重解がわからない人は重解とは何かについて解説した記事をご覧ください。

このとき、

• ax²+bx+c>0の解は、α以外のすべての実数
• ax²+bx+c<0の解はなし
• ax²+bx+c≧0の解は、すべての実数
• ax²+bx+c≦0の解は、x=α

が成り立ちます。

また、

• （x-α）²>0の解は、α以外のすべての実数
• （x-α）²<0の解はなし
• （x-α）²≧0の解は、すべての実数
• （x-α）²≦0の解は、x=α

となります。

そして、a>0かつ判別式D<0のときは

• ax²+bx+c>0の解は、すべての実数
• ax²+bx+c<0の解はなし
• ax²+bx+c≧0の解は、すべての実数
• ax²+bx+c≦0の解はなし

が成り立ちます。

まずは以上の公式をしっかりと理解しましょう。公式の詳細については二次不等式の解5パターンについて解説した記事をご覧ください。

二次不等式の解き方（判別式の使い分け・見分け方）

以上の公式を理解した上で、ここからは二次不等式の解き方について解説していきます。

解き方の流れとしては以下の通りです。

その1：まずは因数分解できるか考える

二次不等式が与えられたとき、まずは左辺が因数分解できないか考えましょう。

因数分解できるなら、上記でご紹介した以下の4つのどれかに当てはまるので、答えが出せますね。

• （x-α）（x-β）>0の解は、x<α、β<x
• （x-α）（x-β）<0の解は、α<x<β
• （x-α）（x-β）≧0の解は、x≦α、β≦x
• （x-α）（x-β）≦0の解は、α≦x≦β

例えば、x²-10x+16<0という二次不等式が与えられたとします。

まずはx²-10x+16が因数分解できないかを考えます。

すると、（x-2）（x-8）に因数分解できることがわかりますね。

※因数分解のやり方がわからない人は数学1の因数分解について解説した記事をご覧ください。

（x-α）（x-β）<0の解はα<x<βなので、x²-10x+16<0の解は2<x<8となるわけです。

その2：因数分解できないなら解の公式

では、因数分解できない場合はどうすれば良いのでしょうか？そのときは解の公式を使います。

※解の公式がわからない人は解の公式とは何かについて解説した記事をご覧ください。

例えば、二次不等式x²+5x-1<0を考えてみましょう。

x²+6x+2は因数分解できそうにないですね。なので、x²+5x-1に対して解の公式を使います。

解の公式より、x=-3±√3²-2=-3±√7となりますね。

（x-α）（x-β）<0の解はα<x<βなので、解は-3-√7<x<-3+√7となります。

その3：解の公式でD<0になる場合

解の公式を使おうとしたけど、判別式D<0になってしまう場合もあります。

例えば、二次不等式x²+6x+10<0を考えてみましょう。

x²+6x+10は因数分解できそうにないので、解の公式を使います。

しかし、解の公式を使うと判別式D=3²-10=-1<0となってしまい、xを求めることができません。

そうなったときは二次関数y=x²+6x+10のグラフを考えてみましょう。

x²の係数が正で、判別式D<0ということはグラフにすると以下のようなイメージになりますね。

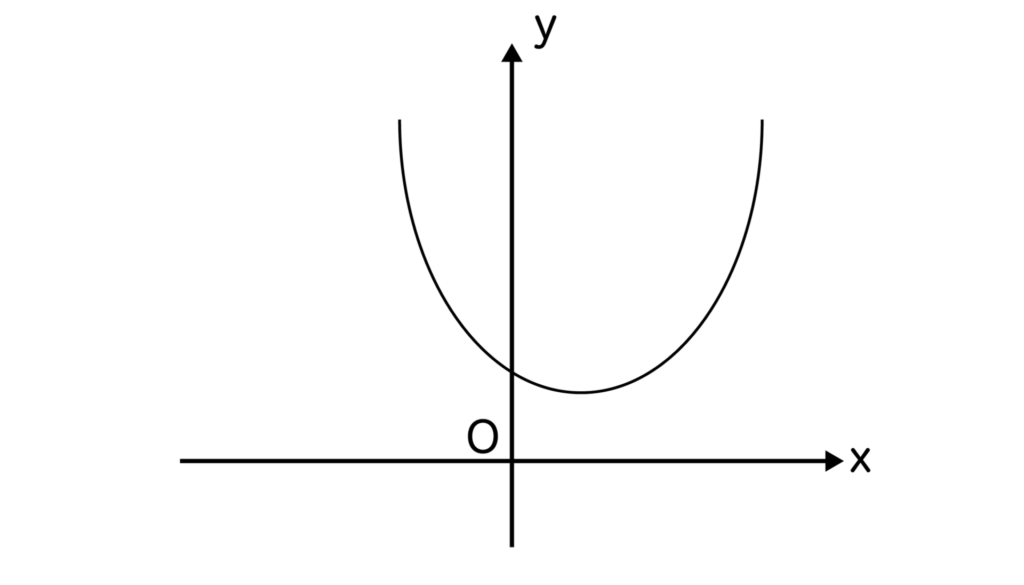
※二次関数のグラフの作成方法について解説した記事もご用意しているので、ぜひ参考にしてください。

判別式D<0よりx軸との接点は1個も存在しません。

以上を踏まえて、x²+6x+10<0つまりy<0になっているところを探しましょう。

y<0になっているところは1つもありませんね。よって二次不等式x²+6x+10<0は解なしとなります。

冒頭でご紹介した公式を見ていただくと、そして、a>0かつ判別式D<0のときは「ax²+bx+c<0の解はなし」となっていることが確認できます。

以上が二次不等式の解き方の流れとなります。

因数分解→解の公式→判別式の確認という流れをしっかり理解しておきましょう。

二次不等式の練習問題

最後に二次不等式の練習問題を解きましょう。

先ほど解説した二次不等式の解き方の流れを意識してみてください。

【練習問題】

以下の二次不等式を解きなさい。

（1）x²-x-6<0

（2）6x²-x-2≧0

（3）-2x²+5x+1≧0

（4）x²-4x+5>0

（5）x²+2x+1>0

【解答＆解説】

（1）x²-x-6を因数分解すると（x+2）（x-3）となりますね。

よって答えは-2<x<3・・・（答）となります。

（2）6x²-x-2を因数分解すると（2x+1）（3x-2）となりますね。

よって答えはx≦-1/2、2/3≦x・・・（答）となります。

（3）x²の係数は正の数である方が解きやすいので、両辺に-1をかけてx²の係数を正にしましょう。

※係数の意味がわからない人は多項式の定義について解説した記事をご覧ください。

すると、2x²-5x-1≦0となりますね。2x²-5x-1は因数分解できそうにないので、解の公式を使います。

解の公式よりx=5±√33 / 4となるので、答えは5-√33 / 4<x<5+√33 / 4・・・（答）となります。

（4）x²-4x+5は因数分解できそうにないので、解の公式を使います。

しかし、解の公式を使おうとすると判別式D=2²-5<0になります。x²の係数が正かつD<0のグラフイメージは以下のようになりますね。

よって、x²-4x+5>0の解は全ての実数・・・（答）となります。

※二次不等式で解が全ての実数になる全ケースをご紹介した記事もぜひ参考にしてください。

（5）x²+2x+1を因数分解すると（x+1）²となりますね。

（x+1）²>0はx=-1以外の全ての実数・・・（答）において成り立つことがわかります。

今回は二次不等式の解き方について解説しました。まずは因数分解できるかを考えてみて、その後に解の公式（判別式）が使えないかを検討してみてください。

また、判別式の使い分け・見分け方に迷ったときはグラフを書くということも意識してみてください。