二等辺三角形の高さは自力で求めることができますか?
二等辺三角形の高さを求めさせる問題は入試では直接出題されることは稀ですが、図形問題を解く上での基礎となるので必ず求められるようにしておかなければなりません。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が二等辺三角形の高さの求め方について図解でわかりやすく解説していきます。
また、高さが求めることで何ができるようになるのか?についても解説していきます。
二等辺三角形の高さの求め方
二等辺三角形の高さは、基本的に
- 頂角を挟む2辺の長さ
- 底辺の長さ
の2つがわかっていれば求めることが可能です。
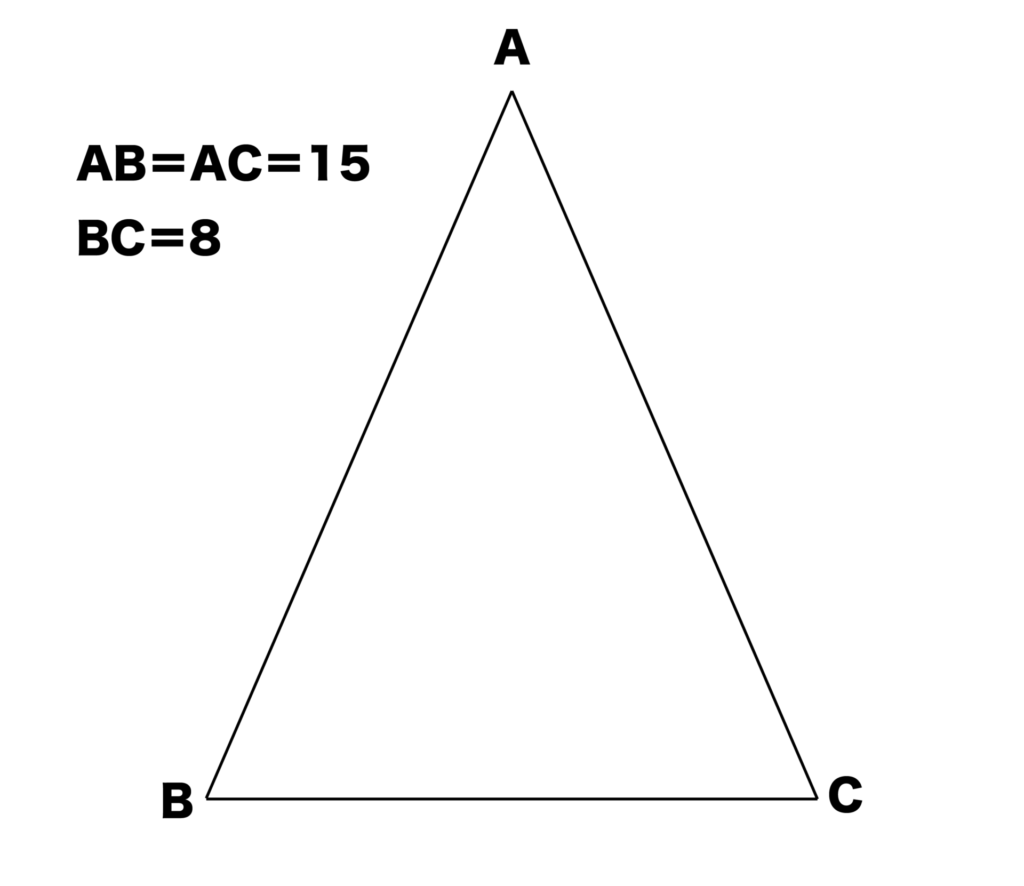
例えば以下の図のようにAB=AC=15、BC=8の二等辺三角形の高さを求めてみましょう。
※頂角を挟む2辺の長さはAB、ACのことで、底角はBCのことです。
二等辺三角形の高さを求めるには、頂角から底辺に対して垂線をおろすのが定石です。
※二等辺三角形の底辺の長さの求め方について解説した記事もぜひ合わせてご覧ください。
以下の図のように点AからBCに垂線をおろし、BCとの交点をDとしてみます。
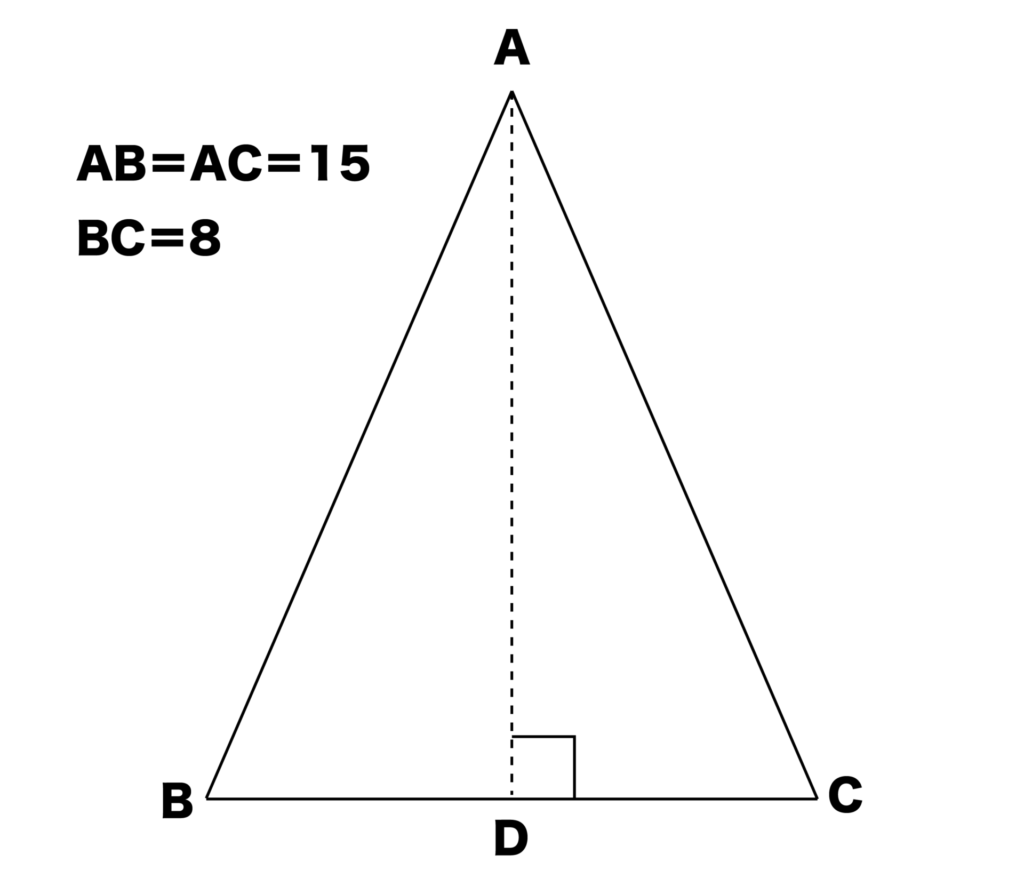
すると、点DはBCの垂直二等分線になるのでした。
※詳しくは二等辺三角形の定義と定理(性質)について解説した記事をご覧ください。
よって、BDはBCの半分の長さになるのでBD=4となります。
ここで、三角形ABDに注目すると、∠BDA=90°より三角形ABDは直角三角形になりますね。
よって、三平方の定理より、AB2+AD2+BD2となります。
AB=15、BD=4より、152=AD2+42となるので、AD2=225-16=209となります。
ここで、AD>0よりAD=√209となります。
※AD=√209となる理由がわからない人は平方根とは何かについて解説した記事をご覧ください。
ADは点AからBCに対しておろした垂線なので、二等辺三角形ABCの高さに相当します。
よって、二等辺三角形ABCの高さ=√209を求めることができました。
二等辺三角形の高さを求めるためには三平方の定理を使うのが定石であるということを必ず頭に入れておきましょう。
二等辺三角形と三平方の定理の関係について解説した記事もご用意しているので、ぜひ参考にしてください。
二等辺三角形の高さを求めると何ができる?
では、二等辺三角形の高さを求めるとどんなメリットがあるのでしょうか?
結論から申しますと、高さを求めることで二等辺三角形の面積を求めることができます。
二等辺三角形の高さを計算(三平方の定理)で求めている時点で、底辺の長さはわかっているはずです。
三角形の面積は底辺×高さ÷2で求められるので、二等辺三角形の面積も当然求めることができるというわけです。
先ほど、以下のAB=AC=15、BC=8の二等辺三角形ABCにおいて、高さAD=√209を求めることができました。

上記の二等辺三角形の面積=BC(底辺)×AD(高さ)÷2=8×√209÷2=4√209となります。
二等辺三角形の高さを求めるのは面積を求めるための手段であるということを頭に入れておきましょう。
二等辺三角形の面積の求め方について詳しく解説した記事もご用意しているので、ぜひ合わせてご覧ください。
頂角=120°と30°の二等辺三角形の高さについて
頂角=120°と30°の二等辺三角形の高さは1辺の長さだけわかれば求めることができます。
これは例外のケースなのでしっかり理解しておきましょう。
まずは頂角=120°のケースから解説します。
頂角=120°の二等辺三角形の高さの求め方
以下の図のように∠A=120°の二等辺三角形ABCにおいては、AB:AC:BC=1:1:√3になります。
※詳しくは二等辺三角形と比の関係について解説した記事をご覧ください。

以上をもとにして、以下の図のように∠A=120°、AB=AC=10の二等辺三角形ABCの高さADを求めてみましょう。
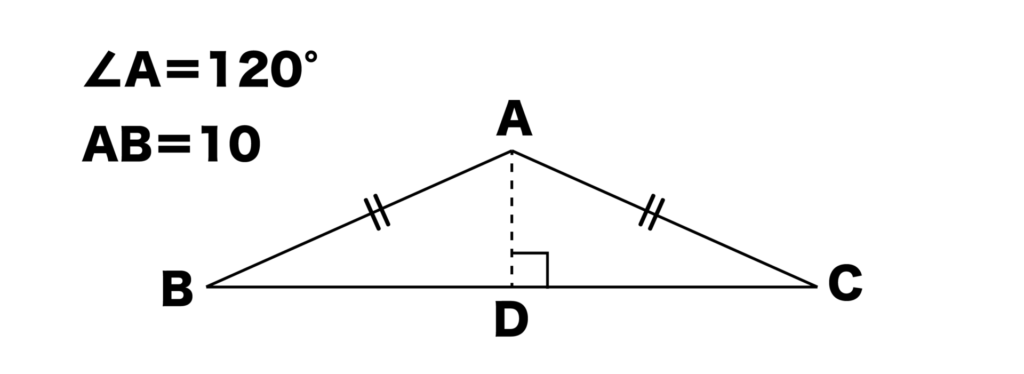
今回はAB(AC)の長さしかわかっていません。
先ほどと同様に考えて、∠BAD=60°、∠BDA=90°ですね。
よって、三角形ABDは60°型の直角三角形になるので、AD:AB:BD=1:2:√3になります。
AB=10なので、二等辺三角形ABCの高さAD=5となります。
また、BD=5√3になるので、BC=10√3となります。
※上記で解説した通り、確かにAB:AC:BC=1:1:√3になっていることがわかります。
頂角=30°の二等辺三角形の高さの求め方
頂角=30°の二等辺三角形も1辺の長さだけわかっていれば高さもわかります。
以下の図のように、∠A=30°の二等辺三角形ABCにおいて、AB:AC:BC=(√2+√6):(√2+√6):2となります。
また、三角形ABDにおいてBD:AD:AB=1:(2+√3):(√2+√6)となります。
※詳しくは二等辺三角形と比の関係について解説した記事をご覧ください。
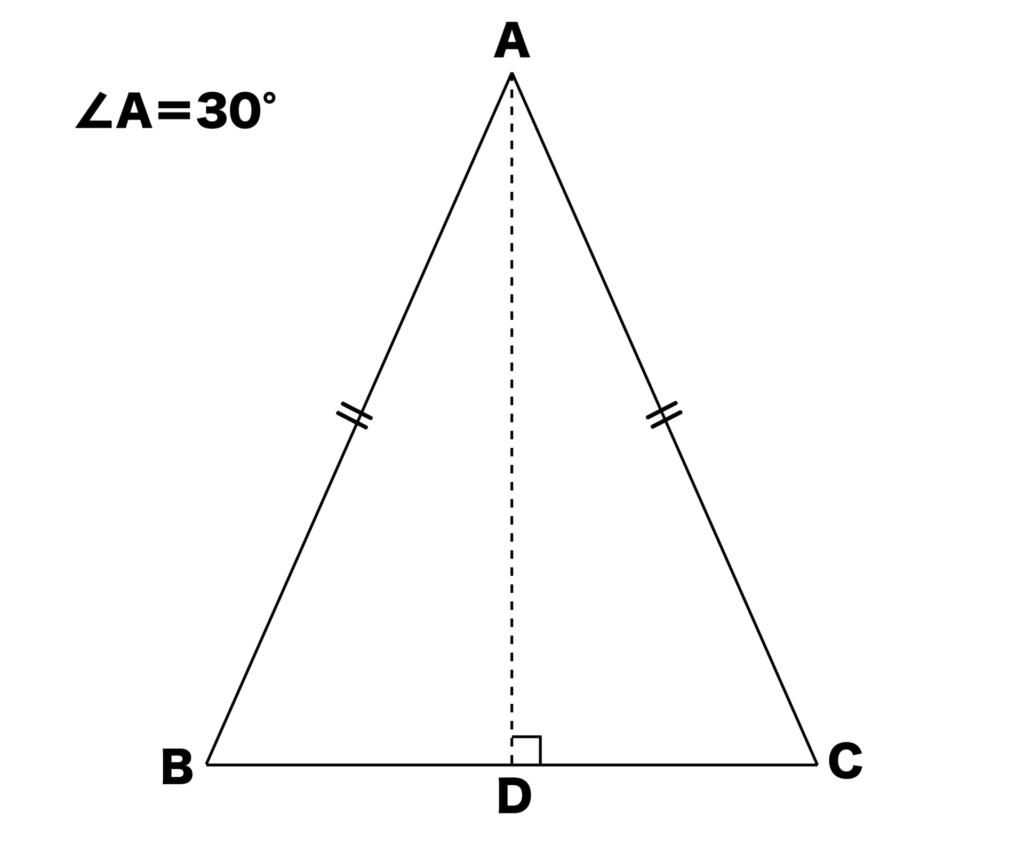
では、以上の∠A=30°の二等辺三角形ABCにおいてAB=AC=20のときの高さADを求めてみましょう。
AB:AD=(√2+√6):(2+√3)より、
高さAD
=20 × (2+√3)/(√2+√6)
=(40+20√3) / (√2+√6)
=(40+20√3)(√2-√6) / (√2+√6)(√2-√6)
=5√2+5√6
となります。
頂角=120°と30°の二等辺三角形の高さは1辺だけがわかっていれば求めることができるということをしっかり頭に入れておきましょう。
直角二等辺三角形の高さの求め方
最後に、直角二等辺三角形の高さの求め方について解説します。
まず、直角二等辺三角形の辺の比は以下の図のように1:1:√2になるのでした。これは暗記必須なので必ず覚えておきましょう。
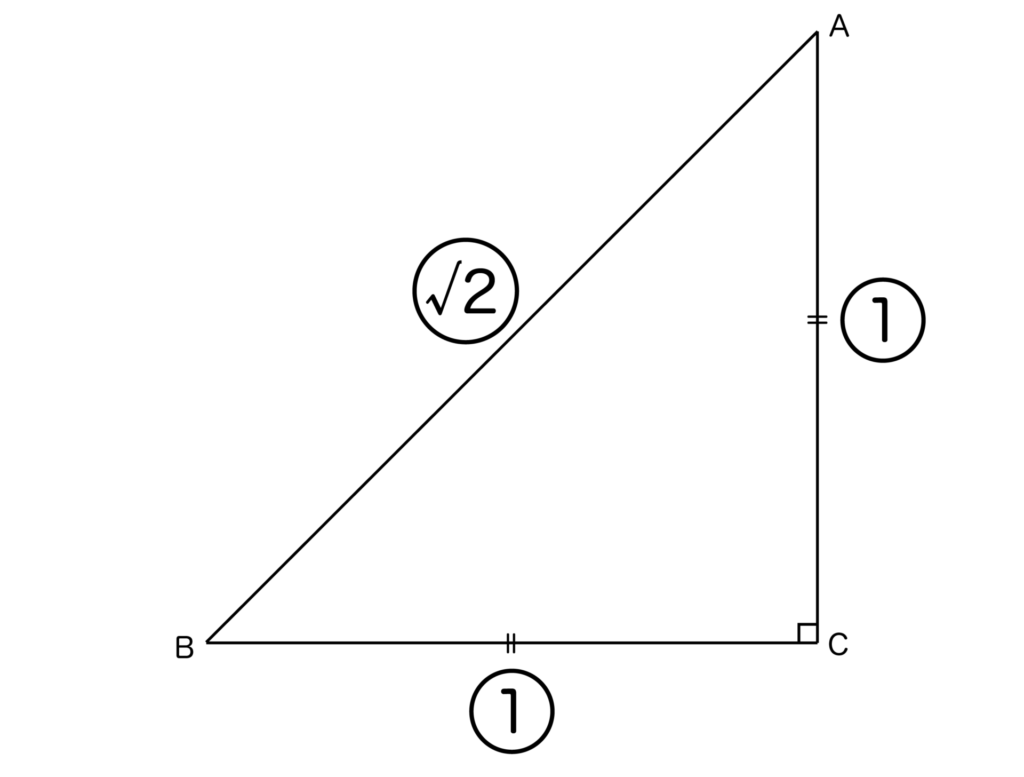
ACまたはBCがわかっている場合はそれがそのまま高さになるので問題ないでしょう。
では、ABの長さだけわかっている場合はどうでしょうか?
上記の図においてAB=30としてみましょう。
すると、AB:AC=√2:1より、高さAC=30/√2=15√2となります。
直角二等辺三角形は1辺(斜辺)の長さがわかれば高さも必ず求めることができます。
直角二等辺三角形の辺の長さについて詳しく解説した記事もご用意しているので、ぜひ合わせてご覧ください。
今回は二等辺三角形の高さの求め方について解説しました。
頂角=120°と30°の二等辺三角形と直角二等辺三角形以外の二等辺三角形は高さを求めるためには頂角を挟む2辺の長さと底辺の長さの2つが必要であるということを必ず理解しておきましょう。
二等辺三角形の辺の長さの求め方を図解でわかりやすく解説した記事もぜひ参考にしてみてください。