二次関数のグラフの作成方法を図解で解説！分数があるときの作成のコツもご紹介

高校数学の数学1で二次関数を学習し始めると、二次関数のグラフを作成する機会も多くなります。

二次関数のグラフ作成は大学入試や共通テストでも必ずと言っていいほど行うので、必ず作成できるようにしておきましょう。

今回は早稲田大学教育学部数学科を卒業した筆者が二次関数のグラフの作成方法について図解で丁寧に解説していきます。

二次関数に分数が入っているときのグラフ作成のコツもご紹介しているので、ぜひ最後までお読みください。

二次関数のグラフ作成にあたっての事前知識

まずは二次関数のグラフを作成するにあたっての事前知識をご紹介します。

まず、二次関数のグラフは必ず放物線状になります。一次関数のように直線になることはありません。

※一次関数とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。

そして、y=ax²+bx+cという二次関数があるとき、a>0ならばグラフは以下のように谷形の形状になり、これを下に凸と言います。

※凸は「とつ」と読みます。

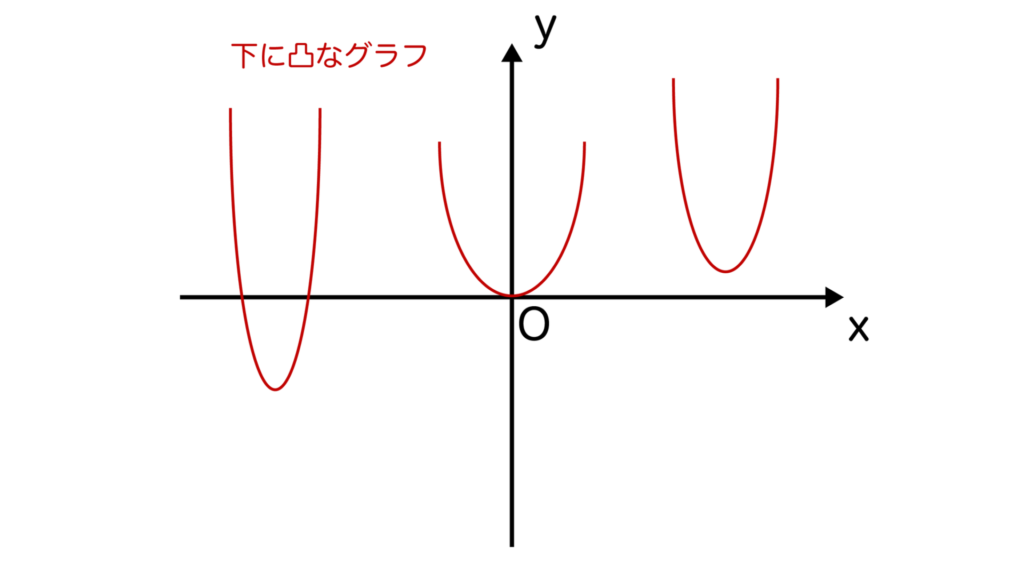
a<0ならば上に凸といい、以下のように山形の形状になります。

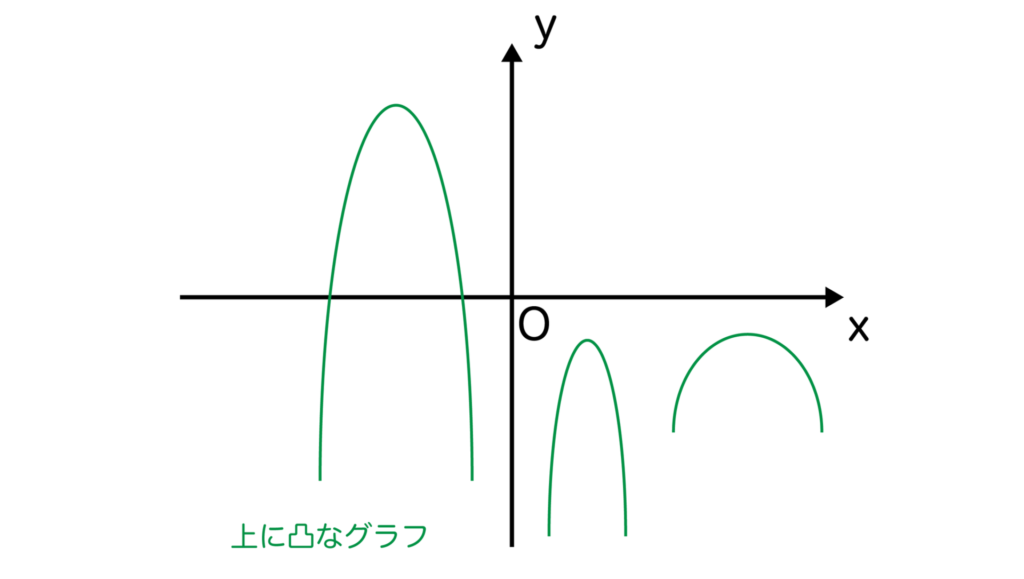
なので、二次関数のグラフを作成するときはaの値が正か負かをしっかり確認し、上に凸なグラフなのか下に凸なグラフなのかを見極めましょう。

二次関数のグラフの作成方法

ここからは二次関数のグラフの作成方法について手順を踏んで解説していきます。

今回は、二次関数y=x²+2x+3のグラフを作成してみましょう。

手順1：頂点の座標を求める

二次関数のグラフを作成するためには、まずは頂点の座標を求めます。

y=x²+2x+3を平方完成するとy=（x+1）²+2となりますね。

※平方完成がわからない人は平方完成のやり方について解説した記事をご覧ください。

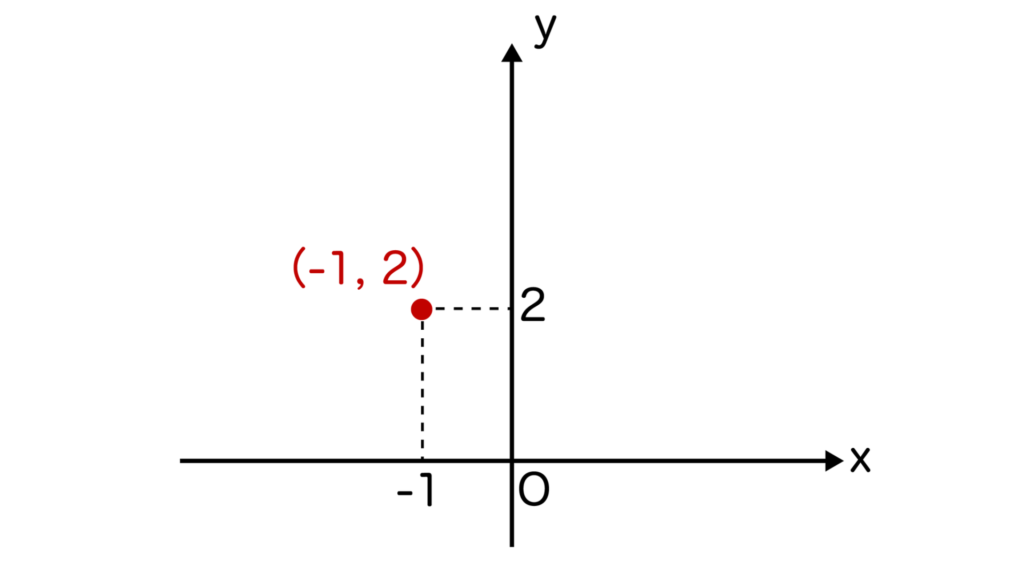
したがって、頂点の座標は（-1、2）となります。

※頂点の座標の求め方について解説した記事もご用意しているのでぜひ合わせてご覧ください。

そして、頂点の座標をグラフに書き込みましょう。

手順2：y切片を求める

続いてはy=x²+2x+3のy切片を求めましょう。y切片はx=0のときのyの値でした。

※詳しくは二次関数の変化の割合の公式！傾き・切片も秒でわかる！をご覧ください。

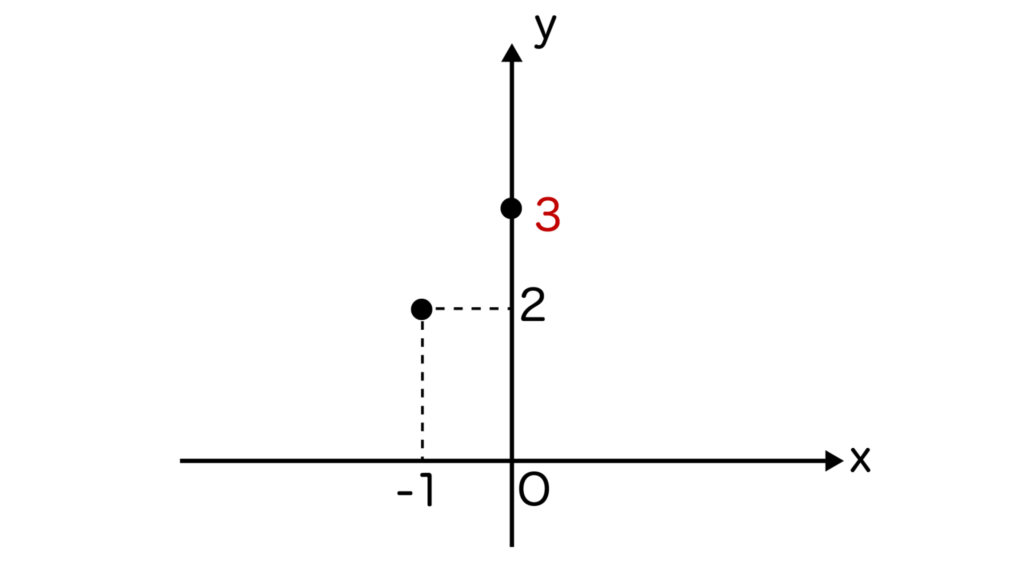
y=x²+2x+3にx=0を代入するとy=3ですね。つまり、y切片が3になります。

点（0、3）をグラフに書き込みましょう。

手順3：軸で左右対称になるようにグラフを書く

二次関数で頂点から式を求める方法について解説した記事をご覧いただくとわかりますが、二次関数は頂点の座標ともう1点の座標さえ決まれば式を決定できます。

つまり、二次関数のグラフを作成するためには頂点の座標と、その二次関数が通るもう1点の座標さえわかればグラフは書けます。

以上で頂点（-1、2）と（0、3）を求めることができたので、グラフを書くための材料は揃いました。

あとは軸で左右対称になるようにグラフを書けばy=x²+2x+3のグラフは完成です。

※二次関数の軸は頂点のx=頂点のx座標のことでしたね。今回の軸はx=-1となります。

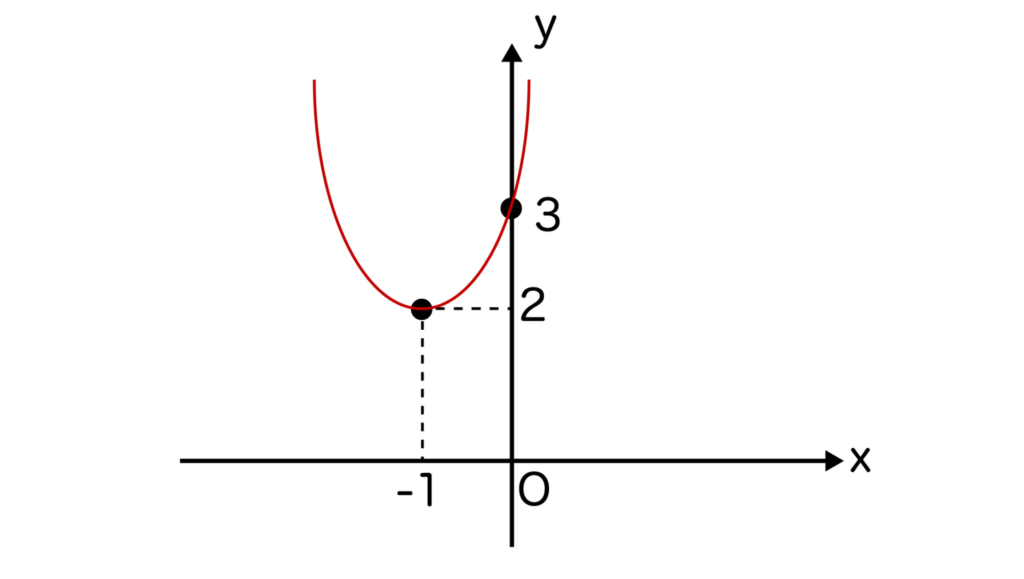
y=x²+2x+3は下に凸のグラフであることに注意しておください。

二次関数の式に分数が含まれているときのグラフの作成方法

先ほどはy=x²+2x+3という比較的シンプルな二次関数でしたが、y=1/2x²+1/4x+5のように式に分数が入っている場合はどうやってグラフを作成すれば良いのでしょうか？

結論から申しますと、先ほどご紹介した手順1〜3を踏んでいただければ問題なくグラフは作成できます。

しかし、二次関数の式に分数が入っている場合は手順1の頂点を求める作業（平方完成）が少し面倒ですね。

そんなときは頂点の座標の公式を使いましょう。

二次関数y=ax²+bx+cがあるとき、頂点の座標は（-b/2a、-（b²-4ac）/4a）となるのでした。

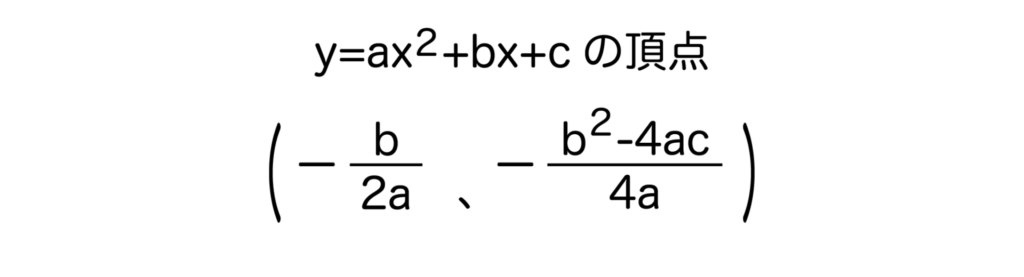
今回はこの公式を使ってy=1/2x²+1/4x+5のグラフを書いてみます。

頂点の座標は（ -1/4 / 2×(1/2) 、-(1/4)²-4×1/2×5 / 4×1/2 ）＝（-1/4、159/32）となりますね。

-1/4＝-0.25、159/32＝4.96…なので、座標の位置としては以下のようになります。

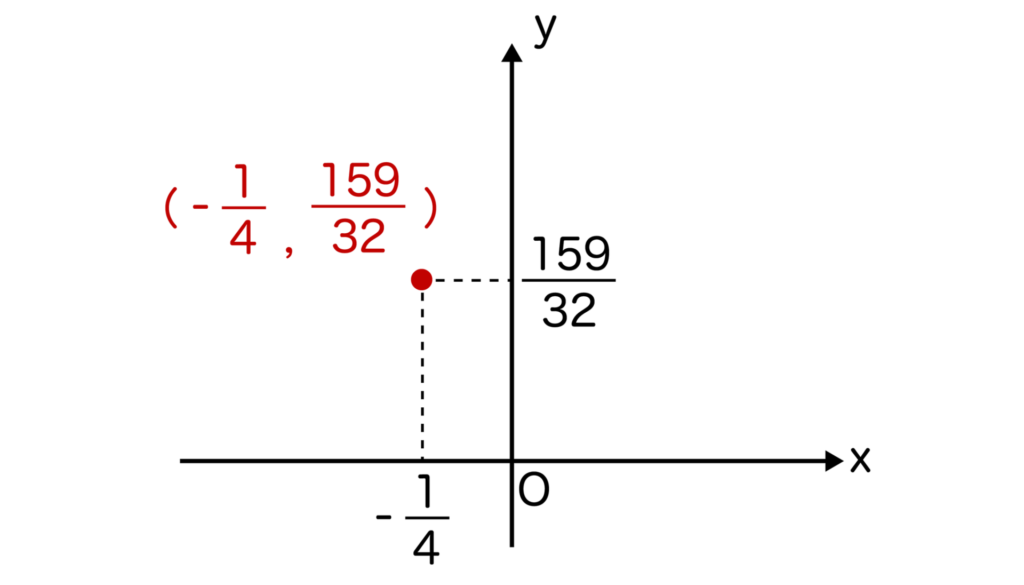
そして、次はy切片を求めます。x=0をy=1/2x²+1/4x+5に代入してy=5が求まります。

（0、5）をグラフに書き込みます。

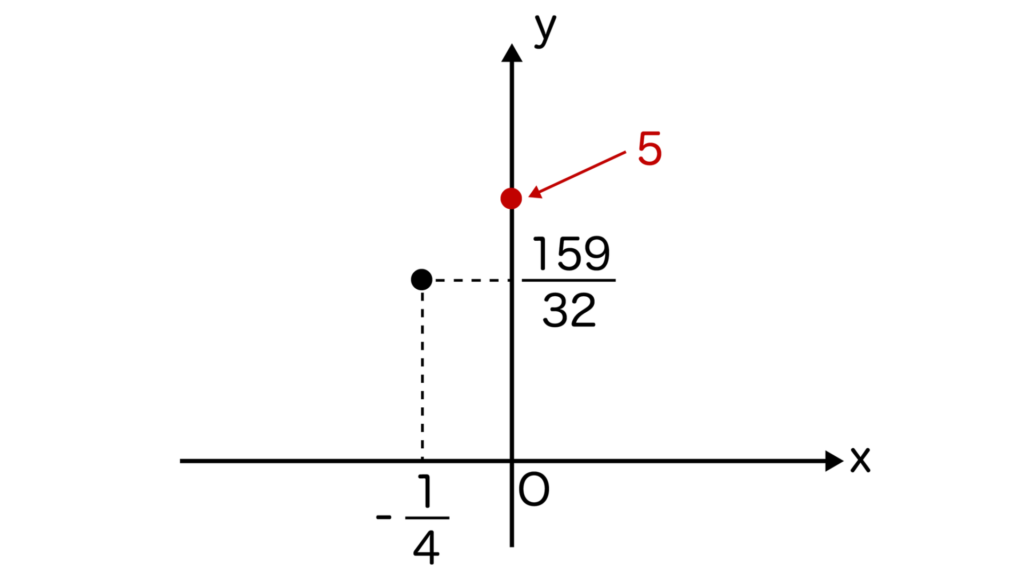
そして、軸で左右対称になるように頂点とy切片を結んでグラフの作成は完了です。

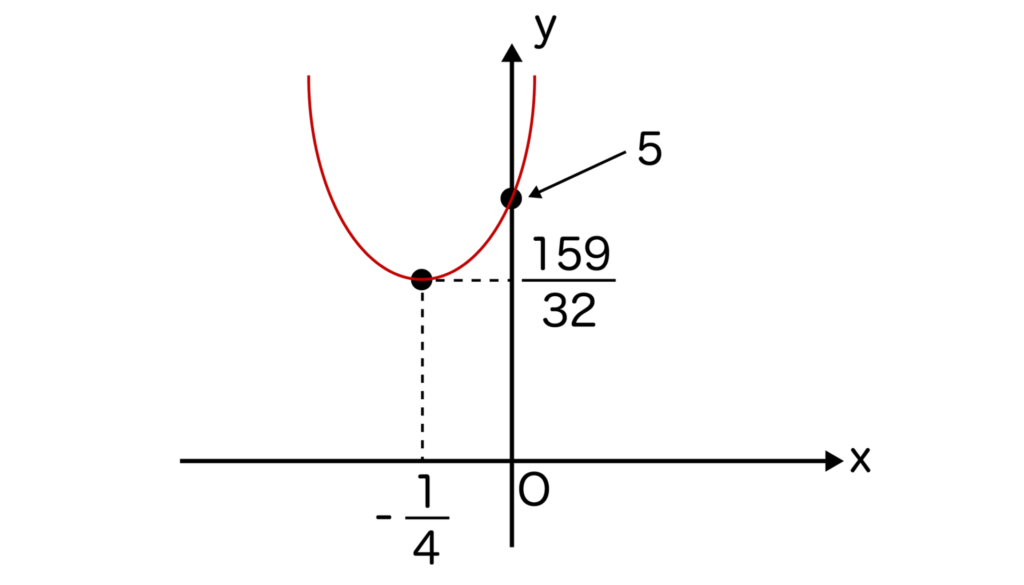
今回もグラフは下に凸であることに注意してください。

二次関数のグラフの作成（練習問題）

最後に、練習として二次関数のグラフをもう1つ作成してみましょう。

【練習問題】

二次関数y=-x²+6x-5のグラフを作成せよ。

【解答＆解説】

今回は平方完成が簡単にできそうなので、平方完成を使って頂点の座標を求めましょう。

-x²+6x-5を平方完成すると、-（x-3）²+4となるので頂点の座標は（3、4）となります。

y切片はx=0を代入して-5となりますね。

今回はy=ax²+bx+cのaがマイナスであることにご注意ください。a<0なので、上に凸な二次関数のグラフになります。

頂点（3、4）と点（0、-5）を通るように上に凸かつ軸で左右対称になるようにグラフを書くと以下のようになります。

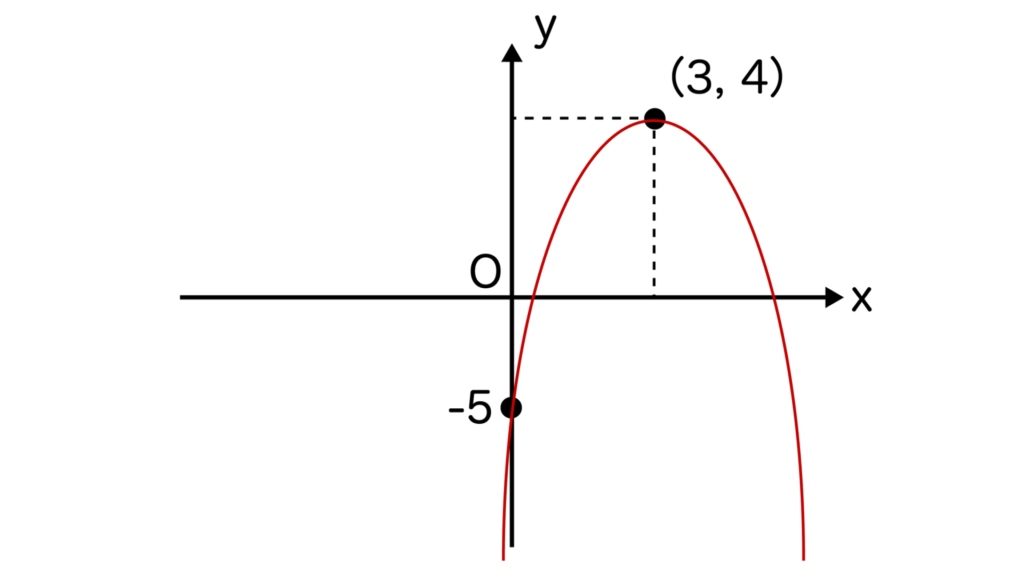
いかがでしたでしょうか？今回は二次関数のグラフの書き方について解説しました。

繰り返しにはなりますが、今回ご紹介した手順をしっかりと頭に入れた上で、上に凸なグラフか下に凸なグラフかに注意しながらグラフの作成を行いましょう。