高校数学の数学1におけるデータの分析の序盤に登場するのが度数分布表です。
度数分布表はデータの分析や統計において極めて重要な用語の1つなので必ず理解しておかなければなりません。
今回は早稲田大学教育学部数学科を卒業した筆者が度数分布表とは何かについて解説するのはもちろんのこと、度数分布表とヒストグラムの関係や階級値など度数分布表と一緒に必ず知っておくべき用語も取り上げます。
数学やデータの分析が苦手な高校生向けにわかりやすく解説していくので、ぜひ最後までお読みください。
度数分布表とは?
データがたくさんあるときは、そのデータをわかりやすく表にまとめるなどして全体の傾向をつかむことが大事です。このときに作る最も基本的な表が度数分布表です。
例えば、ある学校のクラス(20人)で数学のテストを行い、その結果が以下のようにまとまっているとします。
ある学校のクラス(20人)の数学のテストの点数(100点満点)
| 57 | 67 | 49 | 52 | 50 |
| 26 | 78 | 66 | 83 | 90 |
| 51 | 45 | 46 | 39 | 85 |
| 79 | 44 | 59 | 65 | 81 |
以上のような表だと全体の傾向をつかみにくですよね。そこで、以下のような表にしてみます。
| 階級[点] | 階級値[点] | 度数[人] | 相対度数 | 累積相対度数 | |
|---|---|---|---|---|---|
| 1 | 20以上30未満 | 25 | 1 | 0.05 | 0.05 |
| 2 | 30以上40未満 | 35 | 1 | 0.05 | 0.10 |
| 3 | 40以上50未満 | 45 | 4 | 0.20 | 0.30 |
| 4 | 50以上60未満 | 55 | 5 | 0.25 | 0.55 |
| 5 | 60以上70未満 | 65 | 3 | 0.15 | 0.70 |
| 6 | 70以上80未満 | 75 | 2 | 0.10 | 0.80 |
| 7 | 80以上90未満 | 85 | 3 | 0.15 | 0.95 |
| 8 | 90以上100未満 | 95 | 1 | 0.05 | 1.00 |
| 合計 | ・・・ | 20 | 1.00 | ・・・ |
今回はデータ(=テストの点数)を8個の区間に分割して以上のような表を作ってみました。
このように、データを複数の区間に分割し、それぞれの区間にデータが何個存在するかを調べ上げた表のことを度数分布表と言います。
度数分布表を使うことでデータが見やすくなり、全体の傾向をつかみやすくなるというメリットを得ることができます。
階級値など、度数分布表と合わせて知っておきたい用語
以上の度数分布表の2列目や3列目に「階級」や「階級値」といった言葉が登場していますが、ここからは以上の度数分布表を用いて、度数分布表と合わせて知っておきたい用語を解説していきます。
階級
1つ目は階級です。上記の度数分布表の2列目に該当します。
階級とはデータを分けたグループのことをいいます。
例えば、度数分布表の「20以上30未満」は「20点以上30点未満」を表しており、「20点以上」なので20点は含まれますが、「30点未満」なので30点は含まれません。
30点は階級「30以上40未満」に含まれます。
階級値
階級値とは、各階級の中央の値のことです。上記の度数分布表の3列目に該当します。
度数分布表を作ると、1つ1つの具体的なデータが見れなくなってしまうというデメリットがあります。
例えば、60点以上70点未満の階級には「67点、66点、65点」の3つのデータが含まれていますが、このような具体的な点数は度数分布表からはわかりません。
そこで、度数分布表ではこの階級に入っている3つのデータはすべて階級値=65であると考えます。
65は60と70のちょうど中央の値ですね。つまり、階級値はその階級を代表する値といえます。
度数
度数とは各階級に含まれるデータの個数のことです。上記の度数分布表の4列目に該当します。
例えば、80点以上90点未満の階級には「83点、85点、81点」という3つのデータが含まれているので、80点以上90点未満の階級の度数=3となるわけです。
特に難しいことは何もないと思います。
度数を数えるときは、数え間違いがないように「正」の文字を利用したり、「タリィチャート」を利用することをおすすめします。
相対度数
相対度数とは、その階級の度数をデータの総数で割った値のことです。上記の度数分布表の5列目に該当します。
例えば40以上50未満の階級には「49点、45点、46点、44点」の4つのデータが含まれているので度数=4となります。
また、データは今回全部で20個あるので、40以上50未満の階級の相対度数=4÷20=0.20となるわけです。
ちなみにですが、相対度数は100倍すると全体の中でその階級が何%を占めているかを知ることができます。
先ほど、40以上50未満の階級の相対度数=4÷20=0.20と求めましたが、0.20×100=20なので、40以上50未満の階級は全体の20%を占めていることがわかります。
累積相対度数
累積相対度数とはその階級以下の相対度数の合計のことです。上記の度数分布表の6列目に該当します。
例えば、50以上60未満の階級以下の相対度数は、
- 20以上30未満=0.05
- 30以上40未満=0.05
- 40以上50未満=0.20
- 50以上60未満=0.25
なので、50以上60未満の階級の累積相対度数=0.05+0.05+0.20+0.25=0.55となるのです。
累積相対度数は度数や相対度数よりも重要な意味を持つ場合があります。
例えば、テストを受験した生徒は自分と同じ階級に全体のどれくらいの割合の生徒がいるのかよりも、自分が上位または下位何%にいるのかを知りたいことの方が多いはずです。
このような場合は累積相対度数を見れば良いのです。
例えば、50以上60未満の階級の累積相対度数は先ほどの通り0.55なので、60点未満の生徒は全体の55%(0.55×100より)を占めていることがわかります。
度数分布表と平均値・中央値・最頻値の求め方
度数分布表を利用して平均値・中央値・最頻値を求める問題はよく出題されるので、解き方を覚えておきましょう。
まずは先ほどの度数分布表を以下に掲載します。
| 階級[点] | 階級値[点] | 度数[人] | 相対度数 | 累積相対度数 | |
|---|---|---|---|---|---|
| 1 | 20以上30未満 | 25 | 1 | 0.05 | 0.05 |
| 2 | 30以上40未満 | 35 | 1 | 0.05 | 0.10 |
| 3 | 40以上50未満 | 45 | 4 | 0.20 | 0.30 |
| 4 | 50以上60未満 | 55 | 5 | 0.25 | 0.55 |
| 5 | 60以上70未満 | 65 | 3 | 0.15 | 0.70 |
| 6 | 70以上80未満 | 75 | 2 | 0.10 | 0.80 |
| 7 | 80以上90未満 | 85 | 3 | 0.15 | 0.95 |
| 8 | 90以上100未満 | 95 | 1 | 0.05 | 1.00 |
| 合計 | ・・・ | 20 | 1.00 | ・・・ |
では、以上の度数分布表から平均値・中央値・最頻値を求めていきましょう。
平均値
まずは平均値からです。度数分布表を使って平均値を求めるやり方は
- 各階級の階級値を求める
- 各階級の階級値×度数を求める・・・(※)
- (※)÷度数の合計を求める
の3ステップです。1の「各階級の階級値を求める」はすでにできているので、割愛します。
次は、各階級の階級値×度数を求めてみましょう。
例えば、20以上30未満の階級は階級値=25で度数=1なので、25×1=25となります。
同様に考えて、30以上40未満の階級は35×1=35、40以上50未満の階級は45×4=180となります。
すべての階級の階級値×度数を計算すると、
25×1+35×1+45×4+55×5+65×3+75×2+85×3+95×1
=25+35+180+275+195+150+255+95
=1210
となりますね。そして、最後は1210を度数の合計(=データの個数)である20で割れば良いので、
平均値=1210÷20=60.5・・・(答)となります。
※度数分布表の平均値の求め方について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
中央値
続いては中央値を求めましょう。
今回は度数の合計(=データの個数)が20個で偶数なので、データを小さい順に並べたときの真ん中(=中央)には10番目と11番目の2つのデータがあります。
まずは10番目と11番目の2つのデータがどの階級に存在するかを調べます。
40以上50未満の階級までには、度数が1+1+4=6であることがわかります。
50以上60未満の階級の度数は5なので、10番目と11番目の2つのデータは50以上60未満の階級に含まれることがわかります。
50以上60未満の階級値は55なので、中央値=(55+55)/2=55・・・(答)となります。
度数分布表の中央値の求め方について詳しく解説した記事もぜひご覧ください。
最頻値
度数分布表における最頻値とは最も度数が高い階級の階級値のことです。
上記の度数分布表において最も度数が高いのは50以上60未満の階級ですね(度数=5)
よって、最頻値=50以上60未満の階級の階級値=55・・・(答)となります。
度数分布表を使って最頻値を求めるときは、最も高い度数を答えにしてしまわないようにご注意ください。
度数分布表の最頻値の求め方について詳しく解説した記事もぜひ合わせてご覧ください。
ちなみにですが、以上の平均値・中央値・最頻値の3つを合わせて代表値と呼ぶので覚えておきましょう。
度数分布表の作り方!階級の幅とは?
以上で度数分布表がどんなものかはご理解いただけたかと思います。
ここからは度数分布表の作り方の手順を簡単に解説していきます。
手順としては以下の4ステップとなります。
- 階級の幅を決める
- 各階級に含まれるデータの度数を数える
- 各階級の階級値を計算する
- 相対度数と累積相対度数を計算する
まずは階級の幅を決めることからです。階級の幅とは階級をどれくらいの大きさで区切るかということです。
例えば上記の度数分布表では20以上30未満や50以上60未満のように、10で区切って階級を作っていました。この10のことを階級の幅といいます。
階級の幅は10である必要はまったくありません。5でも20でも問題ありません。しかし、どの階級でも階級の幅は同じにするようにするのが一般的なので、その点だけ注意しましょう。
階級の幅を決めたら、各階級に含まれるデータの度数(=個数)を数えましょう。数えるときは上記でもご紹介した「正」の文字や「タリィチャート」を利用するのがおすすめです。
その後は各階級の階級値、相対度数と累積相対度数を計算し、以上を表にするだけです。
以上が度数分布表の作り方となります。
度数分布表とヒストグラム
度数分布表はわかりやすい表ではあるのですが、さらにわかりやすくするために度数分布表をヒストグラムに表す場合があります。
再度、先ほどの度数分布表を以下に掲載します。
| 階級[点] | 階級値[点] | 度数[人] | 相対度数 | 累積相対度数 | |
|---|---|---|---|---|---|
| 1 | 20以上30未満 | 25 | 1 | 0.05 | 0.05 |
| 2 | 30以上40未満 | 35 | 1 | 0.05 | 0.10 |
| 3 | 40以上50未満 | 45 | 4 | 0.20 | 0.30 |
| 4 | 50以上60未満 | 55 | 5 | 0.25 | 0.55 |
| 5 | 60以上70未満 | 65 | 3 | 0.15 | 0.70 |
| 6 | 70以上80未満 | 75 | 2 | 0.10 | 0.80 |
| 7 | 80以上90未満 | 85 | 3 | 0.15 | 0.95 |
| 8 | 90以上100未満 | 95 | 1 | 0.05 | 1.00 |
| 合計 | ・・・ | 20 | 1.00 | ・・・ |
最も基本的なヒストグラムは階級と度数を使って作ることができます。
以上の度数分布表の階級と度数に注目してヒストグラムを作ると、以下のようになります。
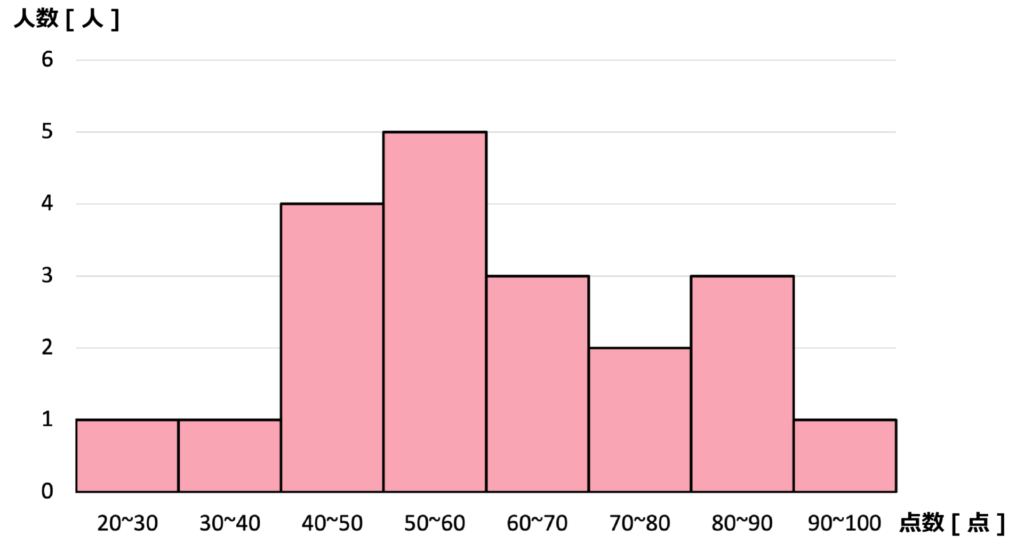
各柱の横の長さ=1とすると、柱の面積が各階級の度数を表しています。
例えば、60~70の階級の柱に注目すると、横の長さ=1、縦の長さ=3なので、この柱の面積は1×3=3となります。
60~70の階級の度数は確かに3であることが確認できます。
ちなみに、上記のヒストグラムの横軸は階級を記載していますが、ヒストグラムによっては階級値を記載する場合もあります。
今回は度数分布表とは何かについて解説した後、階級値などの重要用語やヒストグラムの作り方などについて解説していきました。
度数分布表はデータの分析分野の基礎となるので、必ず理解しておきましょう。


