数学Aの確率においてメインテーマとも言えるのが期待値です。
期待値は大学入試や共通テストでも頻出なので、必ず求め方を理解しておきましょう。
本記事では早稲田大学教育学部数学科を卒業した筆者が期待値とは何か・期待値の意味について解説した後、期待値の求め方や計算方法・公式についてわかりやすく解説していきます。
また、期待値の練習問題も豊富に用意しているので、ぜひ最後までご覧ください。
期待値とは?意味は?公式をご紹介
早速、期待値とは何か・意味について解説していきます。
ある試行の結果によって値の定まる変量Xがあり、Xのとりうる値をx1、x2・・・xnとし、Xがこれらの値をとる確率をそれぞれp1、p2・・・pxとしたとき、
x1p1+x2p2+・・・xnpn
を変量Xの期待値といいます。
※試行=同じ状態のもとで繰り返すことができ、その結果が偶然によって決まる実験や観測のことです。詳しくは同様に確からしいとは何かについて解説した記事をご覧ください。
期待値は英語でexpectationというので、頭文字を取ってEで表されることが多いです。
期待値は平均値と呼ばれることもありますが、大学入試や共通テストでは期待値と呼ばれることがほとんどなので特に覚える必要はありません。
また、変量Xのことを確率変数といいます。
期待値の求め方・計算を例題でわかりやすく解説
以上の期待値の公式だけでは期待値のイメージができないと思うので、ここからは期待値を求める例題を1つご紹介します。
【例題】
2個のサイコロを同時に投げるとき、出る目の和の期待を求めよ。
【解答&解説】
サイコロを2個投げるときは、サイコロの表を書いて問題を解いていくのが定石でした。
※詳しくはサイコロの確率の計算・求め方について解説した記事をご覧ください。
今回は2個のサイコロの和を考えるので、以下のような表を作ってみましょう。
| 和 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
すると、2個のサイコロを投げたときの出た目の和は2〜12のいずれかの整数であることがわかります。
ここで、目の和をX、それをとる確率をPとすると、以下のような表が作れます。
| X | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
よって、求める期待値は
2・1/36+3・2/36+4・3/36+5・4/36+6・5/36+7・6/36+8・5/36+9・4/36+10・3/36+11・2/36+12・1/36
=252/36
=7・・・(答)
となります。以上が期待値の求め方です。公式を見ると一見難しそうですが、例題を解いてみると期待値の求め方自体はそこまで難しくはなかったかと思います。
期待値の基本問題
以上で期待値の求め方・計算方法がわかったところで、ここからは期待値の問題をたくさん解いていきましょう。
まずは基本問題からです。
【問題】
1個のサイコロを投げて、1、2、3の目が出たら2000円を受け取ることができ、4、5、6の目が出たら500円を払わなければならないゲームがある。このゲームの参加料が300円のとき、このゲームに参加うすることは得と言えるかどうか調べよ。
【解答&解説】
サイコロを1回投げて1、2、3の目が出る確率は3/6=1/2ですね。
4、5、6の目が出る確率も1/2です。
よって、このゲームの期待値は
2000・1/2+(-500)・1/2=1000-250=750[円]
となります。これは参加料の300円よりも高いので、このゲームに参加することは得であると言えます。
期待値はこのように、賞金がついたゲームに参加することが得かどうかや、どの選択肢を取れば有利かなどを判断するのに役立ちます。特に、期待値が金額で表されるとき、これを期待金額といいます。
上記の問題の場合、期待金額=750円となります。
期待値と図形に関する問題
続いては期待値と図形に関する問題です。
【問題】
1辺の長さが1である正六角形ABCDEFの6つの頂点から異なる3点を無作為に選び、その3点を頂点とする三角形Pを作るとき、三角形Pが直角三角形となる確率を求めよ。
また、三角形Pの周の長さの期待値も求めよ。
【解答&解説】
三角形Pの3つの頂点の選び方は6C3=20[通り]ですね。
※Cの計算方法がわからない人は組み合わせCの計算と公式について解説した記事をご覧ください。
三角形Pが直角三角形となるのは、以下の図のようにPの1辺が正六角形ABCDEFの6つの頂点を通る円の直径になるときですね。
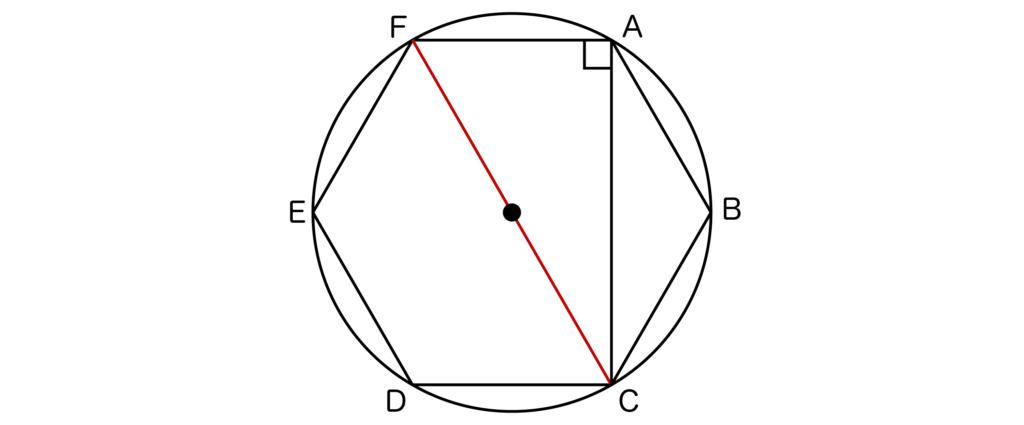
その直径の選び方は3通りあり、各直径に対して直角三角形は4個できるので、求める確率は
3・4 / 20=3/5・・・(答)となります。
次は三角形Pの周の長さの期待値を求めます。
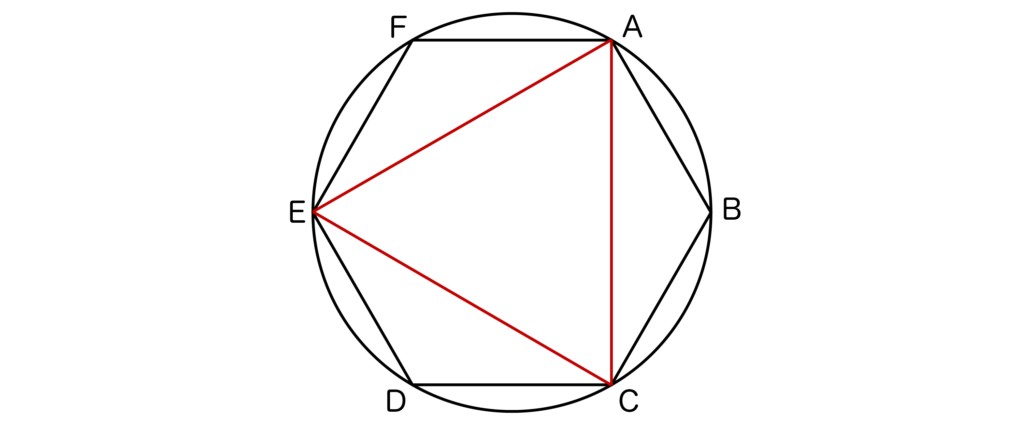
[1]三角形Pが正六角形ABCDEFと辺を共有しないとき
以下の図のようにPは正三角形となり、その場合は2通りあるので求める確率は2/20=1/10となります。
このとき、周の長さは√3×3=3√3となります。
[2]三角形Pが正六角形ABCDEFと1辺だけを共有するとき
先ほどの通り、Pは直角三角形となります。その確率は3/5でした。
このとき、周の長さは1+2+√3=3+√3となります。
[3]三角形Pが正六角形ABCDEFと2辺を共有するとき
以下の図のようにPは二等辺三角形となります。
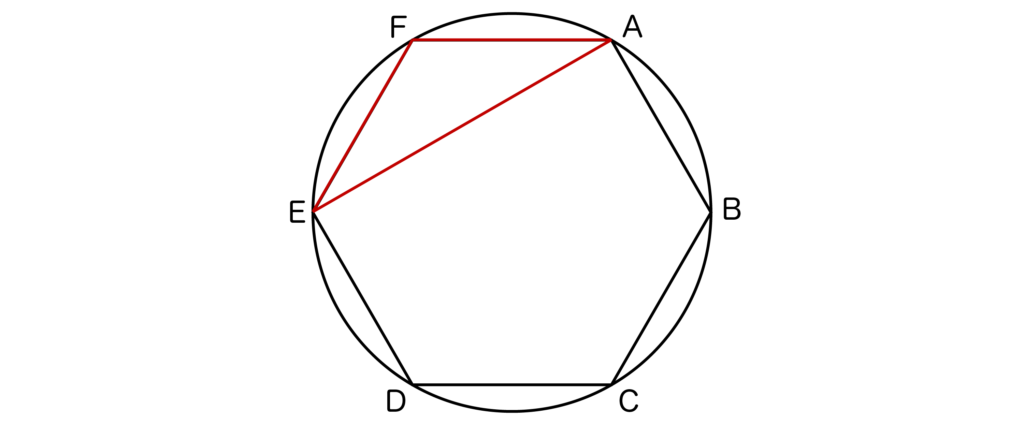
正六角形ABCDEFの頂点を1つ選ぶと、以上のような二等辺三角形が1つ決まるので、この確率は6/20=3/10となります。
周の長さは1+1+√3=2+√3となります。
以上[1]〜[3]より、求める期待値は
3√3・1/10+(3+√3)・3/5+(2+√3)・3/10=(12+6√3)/5・・・(答)となります。
期待値と有利・不利に関する問題
最後は期待値と有利・不利に関する問題です。
【問題】
1個のサイコロを投げて、出た目の数だけ得点がもらえるとする。ただし、出た目の数が気に入らなければ、1回だけサイコロを振り直すことができるものとする。
もらえる得点の期待値が最大になるように振る舞ったとき、その期待値を求めよ。
【解答&解説】
まずはサイコロを1個投げて出る目の期待値を求めましょう。
(1+2+3+4+5+6)・1/6=7/2ですね。
7/2=3.5なので、出た目の数が3以下なら振り直し、4以上ならそのままが良いということがわかります。
1回目に出た目の数をX、振り直しをしたときに、2回目に出た目の数をYとすると、XとYの組み合わせは
(X、Y)=(1、1)(1、2)(1、3)(1、4)(1、5)(1、6)(2、1)(2、2)(2、3)(2、4)(2、5)(2、6)(3、1)(3、2)(3、3)(3、4)(3、5)(3、6)
ですね。よって求める期待値は
(1・1/62+2・1/62+3・1/62+4・1/62+5・1/62+6・1/62+1)・3+4・1/6+5・1/6+6・1/6=17/4・・・(答)となります。
いかがでしたか?
今回は期待値とは何か・意味や求め方について解説した後、期待値の問題を解いていきました。
期待値の問題を解くには確率の問題をしっかりと解けるようにしておかなければなりません。期待値が苦手な人は、確率の分野の復習をしっかりすることをおすすめします。


