二次方程式の重解とは？公式が一目でわかる！練習問題付き

二次方程式の解の公式・判別式を学習すると「重解」という用語が登場します。

重解は大学入試や共通テストでも頻出の用語なので、必ず覚えておく必要があります。

そこで今回は、早稲田大学教育学部数学科を卒業した筆者が二次方程式の重解とは何かについて解説した後、重解の公式や求め方などについて解説していきます。

※二次方程式とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。

二次方程式の重解とは？公式は？

ax²+bx+c=0という二次方程式があったとき、b²-4acのことを判別式といい、Dで表現するのでした。

※詳しくは二次方程式の判別式について解説した記事をご覧ください。

D=b²-4ac=0となるとき、二次方程式ax²+bx+c=0は解を1つだけもち、その解のことを重解といいます。

二次方程式ax²+bx+c=0の解は解の公式より、x=-b±√b²-4ac / 2aとなるのでした。

※詳しくは解の公式について解説した記事をご覧ください。

二次方程式ax²+bx+c=0が重解を持つとき、判別式D=b²-4ac=0なので、x=-b/2aが重解となります。

重解の一例として、二次方程式x²+8x+16=0を解いてみましょう。

x²+8x+16を因数分解すると、（x+4）²となるのでx=-4となります。

※因数分解のやり方がわからない人は、数学1の因数分解について解説した記事をご覧ください。

このとき、判別式D=8²-4×1×16より確かに0となっていることがわかります。

また、重解＝-8/2×1となり、確かに-4になっていることも確認できます。

xの係数が偶数のときの重解

二次方程式ax²+bx+c=0においてxの係数bが偶数のとき、判別式はb’²-acとなり、D/4と表現できるのでした（b=2b’とする）

D/4=0のときも二次方程式ax²+bx+c=0は解を1つだけもち、その解は重解と呼ばれます。

bが偶数の場合、解の公式によりx=-b’±√b’²-ac / aが成り立つのでした（b=2b’とする）

b’²-ac=0のとき、重解はx=-b’/aとなります。

では、例として二次方程式x²+10x+25=0を解いてみましょう。

x²+10x+25＝（x+5）²より、x=-5となります。

このとき、判別式D/4=5²-1×25で確かに0となっていることが確認できます。

また、重解＝-5/1より、こちらも確かに-5となっていることが確認できます。

重解と二次関数のグラフ

二次関数y=ax²+bx+cの判別式D=b²-4acが0となるとき、二次関数y=ax²+bx+cはただ1点でx軸と交わります。

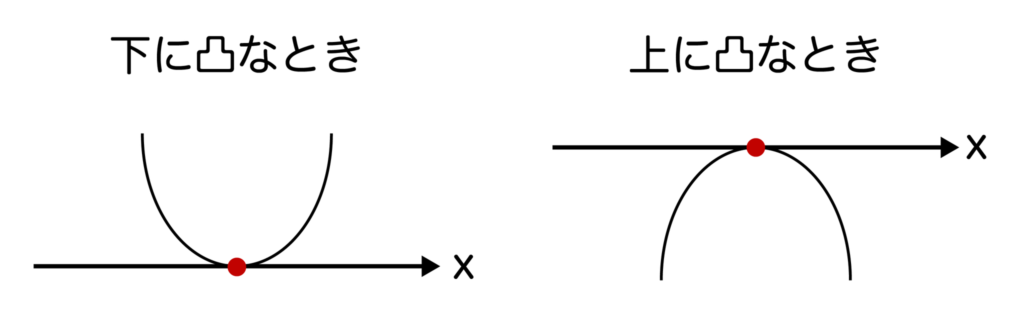
例えば、二次関数y=x²+4x+4を考えてみましょう。

x²+4x+4＝（x+2）²より、x=-2となり、グラフは以下の通りとなります。

※二次関数のグラフの作成方法について解説した記事もご用意しているので、ぜひ参考にしてください。

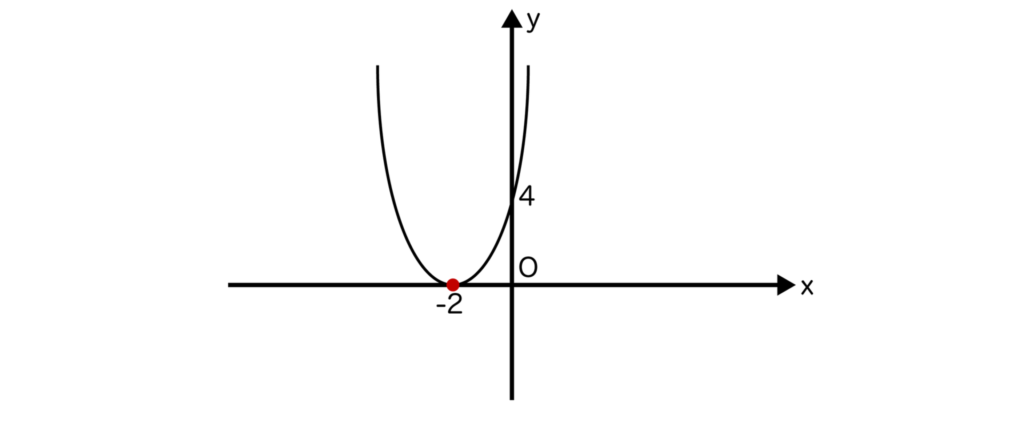
点（-2、0）のみの1点でx軸と接していることがわかります。

このとき、判別式D/4＝2²-1×4より確かに0となっていることがわかります。

重解と二重解の違いとは？

二次方程式ax²+bx+c=0の最高次数は2なので、最高でも2つの異なる解が登場する可能性があります。

3次方程式なら最高でも3つの異なる解が登場する可能性があります。4次方程式、5次方程式でも同様です。

二次方程式において2個の解が同じならば二重解、3次方程式において3個の解が同じならば三重解といいます。4次方程式、5次方程式でも同様です。

なので、重解は二重解、三重解、四重解・・・を含んだ総称と言えます。

しかし、高校数学においては重解＝二重解を指すことがほとんどなので、重解と二重解の違いについてはそこまで気にする必要はありません。

重解に関する練習問題

最後に、重解に関する練習問題をご紹介します。

【練習問題】

（1）二次方程式x²+2（2-m）x+m=0（mは定数）が重解を持つようにmの値を定め、そのときの重解を求めよ。

（2）二次関数y=-x²+4x-4はx軸と共有点を持つか調べ、持つ場合はその座標を求めよ。

（3）二次関数y=x²+2（2-k）x+kがx軸に接するように定数kの値を定めよ。また、そのときの接点の座標を求めよ。

【解答＆解説】

（1）xの係数が2（2-m）で偶数なので、判別式D/4を利用します。

判別式D/4=（2-m）²-1×m=m²-5m+4が0になれば良いので、

（m-1）（m-4）=0より、m=1、4となります。

m=1のとき、もとの二次方程式はx²+2x+1=0となるので、重解はx=-1となります。

m=4のとき、もとの二次方程式はx²-4x+4=0となるので、重解はx=2となります。

（2）y=-x²+4x-4より、判別式D/4=2²-（-1）×（-4）=0となるので、1個の共有点を持つことがわかります。

y=-x²+4x-4=-（x-2）²より、共有点は（2、0）となります。

（3）二次関数がx軸に接するということは重解を持つということなので、

（2-k）²-1×k=0より、k²-5k+4=0

（k-1）（k-4）=0よりk=1、4となります。

二次関数y=x²+2（2-k）x+kの頂点のx座標は-2（2-k）/2×1＝k-2なので、k=1のときx=-1、k=4のときx=2となります。

※二次関数の頂点の座標の求め方について解説した記事もご用意していますので、ぜひ参考にしてください。

よって答えはk=1のとき（-1、0）、k=4のとき（2、0）となります。

今回は二次方程式の重解とは何か？について解説しました。「判別式D=0ならば重解」は必ず覚えておきましょう。