一次関数では変域という概念が登場しますが、変域が何か理解できていない人も多いのではないでしょうか?
※一次関数とは何かについて解説した記事もぜひ合わせてご覧ください。
変域は一次関数の根本の原理から理解すればそこまで難しくはありませんのでご安心ください。
本記事では、早稲田大学教育学部数学科を卒業した筆者が一次関数における変域とは何か・求め方について誰でもわかるようにわかりやすく解説します。
最後には変域に関する問題も用意しているので、ぜひ最後までお読みください。
一次関数の変域とは?
まずは変域とは何かについて解説します。
変域は「変化する領域」の略だと覚えておきましょう。
例えば、y=2x+5という一次関数があったとします。
このとき、値が変化できる(=値を自由に変えられる)のはxとyだけですよね。
x=2ならy=9となりますし、x=-3ならy=-1となります。
では、xが変化できる値を2≦x≦5という領域に限定したらyの値はどうなるでしょうか?
※記号「≦」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。
以下の図の通り、yの値は9≦y≦15に限定されますね。
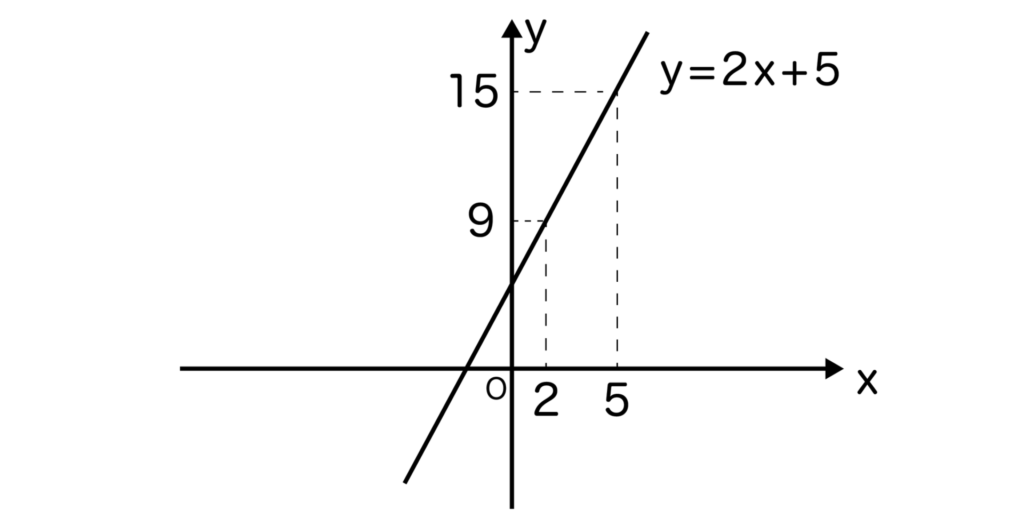
つまり、x・yが変化できる値(=領域)が決まっているとき、それを「xの変域」「yの変域」と言います。
上記の例だとxの変域は2≦x≦5、yの変域は9≦y≦15となります。
また、xの変域のことを定義域、yの変域のことを値域と言います。定義域・値域という用語は大学入試や共通テストでも頻出なので、必ず覚えてください。
一次関数の変域の求め方
一次関数の変域の求め方は難しくありません。では、例題を使って解説していきます。
【例題1】
一次関数y=4x+3において、xの変域が3<x<6のとき、yの変域を求めよ。
【解答&解説】
まずはxがxの変域の端っこの値(今回の場合は3と6)を取ったときのyの値を求めます。
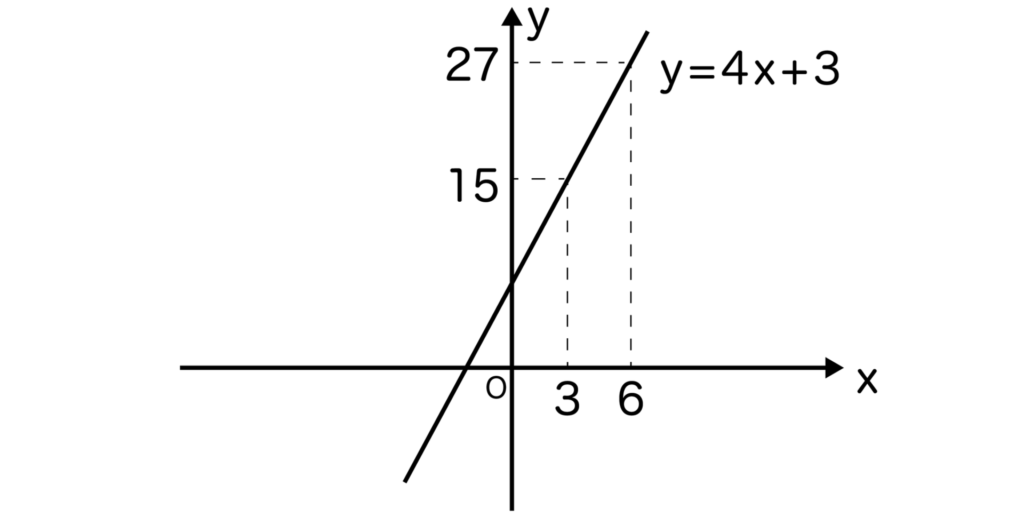
x=3のときy=15、x=6のときy=27ですね。
そして、yの値を小さい順に並べ、間にyを挟んで15<y<27とするだけです。
不等号はxの変域のときに「<」が使われているのでyの変域でも「<」も使用します。
実際にグラフを書いてみても、yの変域が15<y<27になっていることがわかります。
【例題2】
一次関数y=-2x+6において、xの変域が-3≦x≦-1のとき、yの変域を求めよ。
【解答&解説】
こちらも先ほどの例題と同じように解いてみましょう。
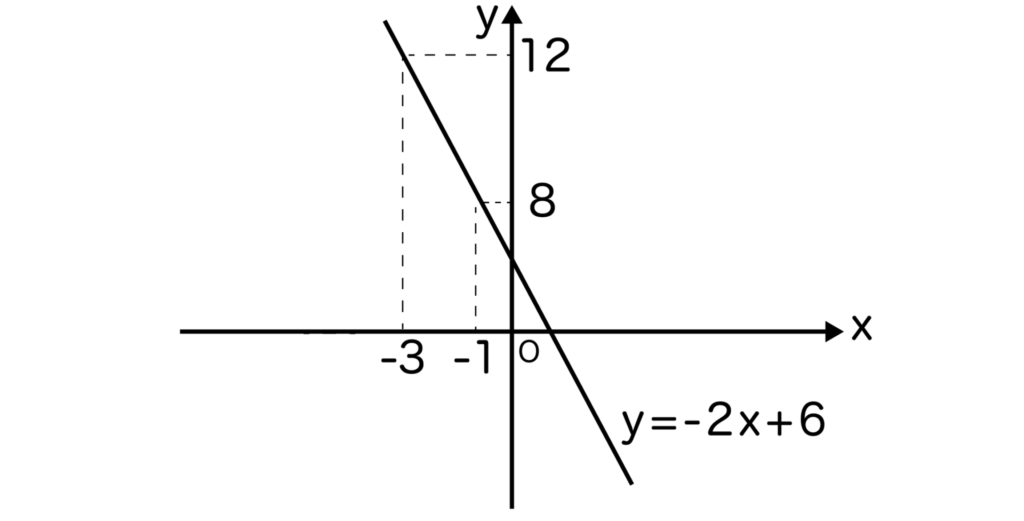
x=-3のときy=12、x=-1のときy=8ですね。
12と8を小さい順に並べて間にyを挟めば良いので、8≦y≦12がyの変域となります。
今回はxの変域が「<」ではなく「≦」だったのでyの変域も「≦」となります。グラフにすると以下のようになります。
xの変域に「<」と「≦」が混ざっているときのyの変域の求め方
では、xの変域に「<」と「≦」が混ざっているとき、yの変域はどうやって求めれば良いでしょうか?
以下の例題で解説していきます。
【例題1】
一次関数y=x+4において、xの変域が3≦x<7のとき、yの変域を求めよ。
【解答&解説】
まずは先ほどと同様にx=3、x=7のときのyの値を求めましょう。
x=3のときy=7、x=7のときy=11ですね。
そして、迷うのが不等号だと思いますが、xの変域は3≦x<7となっており、3に「≦」がくっついている・7に「<」がくっついていると考えます。
そして、x=3のときy=7、x=7のときy=11なので、y=7に「≦」がくっつき、y=11に「<」がくっつくと考えます。
よって、yの変域は7≦y<11となります。
迷ったときは以下のように実際にグラフを書いてももちろんOKです。

もう1つ例題をみてみましょう。
【例題2】
一次関数y=-2x-2において、xの変域が-2<x≦2のとき、yの変域を求めよ。
【解答&解説】
x=-2のときy=2、x=2のときy=-6ですね。
今回は-2に「<」が、2に「≦」がくっついていますね。
よって、y=2に「<」が、-6に「≦」がくっつきます。
したがって、yの変域は-6≦y<2となります。
一次関数の変域に関する練習問題
最後に一次関数の変域をご紹介します。
すべて超基本的な問題なので、全問正解できるまで繰り返し解きましょう。
【練習問題1】
一次関数y=3x+2において、xの変域が-4≦x<-2のとき、yの変域を求めよ。
【解答&解説】
先ほどまで散々解いてきた問題ですね。
x=-4のときy=-10、x=-2のとき-4です。xの変域に注目すると、-4に「≦」が、-2に「<」がくっついているので、y=-10に「≦」が、y=-4に「<」がくっつきます。
よって答えは-10≦y<-4・・・(答)となります。
【練習問題2】
一次関数y=2x+1において、yの変域が7≦y<11のとき、xの変域を求めよ。
【解答&解説】
今度はyの変域からxの変域を求める問題です。やり方は先ほどまでと同じです。
y=7のときx=3、y=11のときx=5ですね。
yの変域に注目すると、7に「≦」が、11に「<」がくっついているので、x=3に「≦」が、x=5に「<」がくっつきます。
よって3≦x<5・・・(答)となります。
今回は一次関数の変域と求め方について解説していきました。変域を求めるときは不等号(≦と<)が混ざるときだけ十分ご注意ください。
わからなくなったらグラフを書いてみることをおすすめします。
一次関数では変化の割合・傾きという重要用語もあります。一次関数の変化の割合・傾きの求め方について解説した記事もご用意しているので、ぜひ合わせてご覧ください。


