二次方程式の判別式とは？いつ使う？具体例で解説！

二次方程式の判別式は大学入試や共通テストでも頻出なので、解の公式とともに必ず覚えておかなくてはならない公式です。

二次方程式の判別式は内容としては難しくないのでご安心ください。

今回は早稲田大学教育学部数学科を卒業した筆者が、二次方程式の判別式とは何かについて解説した後、判別式はいつ使うのか？などについても具体例をあげながら解説していきます。

数学が苦手な人でも理科できるように図解も使っているので、ぜひ最後までお読みください。

※二次方程式とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。

二次方程式の判別式とは？

二次方程式の判別式とは、二次方程式の解の公式x=-b±√（b²-4ac） / 2aにおけるb²-4acのことです。

解の公式のルートの中身＝判別式と覚えておけば問題ありません。

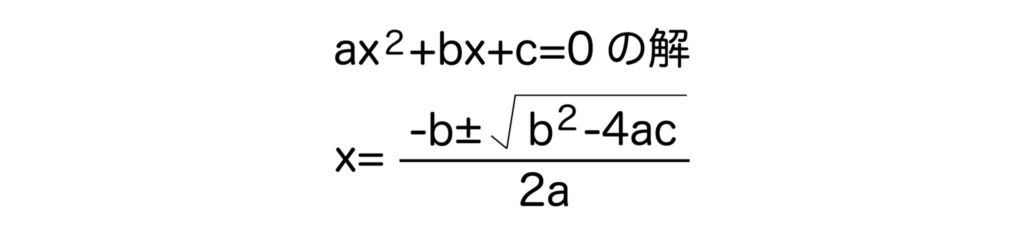
※解の公式がわからない人は、二次方程式の解の公式とは何かについて解説した記事をご覧ください。

判別式はDで表現されることが一般的なため、D=b²-4acとなります。

※判別式は英語で「discriminant」と呼ばれるため、その頭文字を取ってDとなっています。

判別式は大学入試や共通テストでもほぼ毎年出題されているので、必ず覚えておく必要があります。解の公式と一緒にセットで覚えましょう。

二次方程式の判別式の性質

判別式は二次方程式ax²+b+c=0の実数解の個数を調べることに役立ちます。

※実数解とは何かについて詳しく解説した記事もぜひ参考にしてください。

判別式では以下の性質が成り立つので、必ず覚えましょう。

• D>0 ⇔ 異なる2つの実数解を持つ
• D=0 ⇔ ただ1つの実数解を持つ（重解と言います）
• D<0 ⇔ 実数解を持たない

※記号「⇔」の意味がわからない人は必要条件・十分条件について解説した記事をご覧ください。

例えば、x²+5x+6=0という二次方程式があるとします。

このとき、a=1、b=5、c=6より、判別式D＝5²-4×1×6=1となりD>0が成り立つので二次方程式x²+5x+6=0は異なる2つの実数解を持つことがわかります。

実際にx²+5x+6を因数分解すると（x+2）（x+3）となり、解はx=-2、-3なので、確かに異なる2つの実数解を持っていることが確認できます。

※因数分解のやり方がわからない人は数学1の因数分解について解説した記事をご覧ください。

では、x²+6x+9=0の実数解の個数はどうでしょうか？判別式を使って確認します。

a=1、b=6、c=9より、判別式D＝6²-4×1×9=0となり、ただ1つの実数解を持つことがわかります。

x²+6x+9を因数分解してみると、（x+3）²となるので、解は確かにx=-3の1つのみとなっていることがわかります。

※二次方程式において解が1つだけの場合、それを重解といいます。重解について詳しく解説した記事もぜひ合わせてご覧ください。

最後はx²+3x+5=0の実数解の個数を調べてみましょう。

a=1、b=3、c=5より、判別式D=3²-4×1×5=-11となり、D<0になるため実数解を持たないことがわかります。

実際に二次方程式x²+3x+5=0を解の公式を使って解こうとすると、

x=（-3±√3²-4×1×5） / 2×1となり、√の中身がマイナスになってしまうので、確かに実数解を持たないことがわかります。

判別式D/4について

解の公式では二次方程式ax²+bx+c=0において、xの係数であるbが偶数の場合の解はx=-b’±√（b’²-ac） / aとなるのでした。

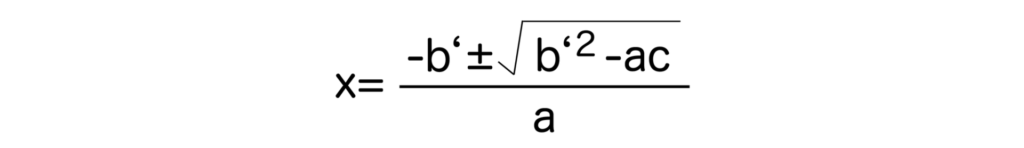
※係数の意味がわからない人は多項式の定義について解説した記事をご覧ください。

先ほども解説した通り、判別式は解の公式のルートの中身のことなので、二次方程式ax²+bx+c=0において、xの係数であるbが偶数の場合、判別式はb’²-acとすることができます（b=2b’とする）

b=2b’の場合、判別式D=b²-4ac=4（b’²-ac）となることから、D/4と表現されることがあります。

つまり、D/4=b’²-acです。DがD/4になっても、判別式の性質自体は変わらず以下の通りとなります。

• D/4>0 ⇔ 異なる2つの実数解を持つ
• D/4=0 ⇔ ただ1つの実数解を持つ（重解と言います）
• D/4<0 ⇔ 実数解を持たない

判別式はいつ使う？

判別式は二次方程式の解の個数を調べることはもちろんのこと、二次関数のx軸との位置関係を調べることにも使えます。

二次関数y=ax²+bx+cがあるとき、x軸との共有点の個数は以下の3パターンに分けられます。

D>0 ⇔ 異なる2点で交わる

判別式D=b²-4ac>0のとき、y=ax²+bx+cはx軸と異なる2点で交わります。グラフで表現すると以下のようになります。

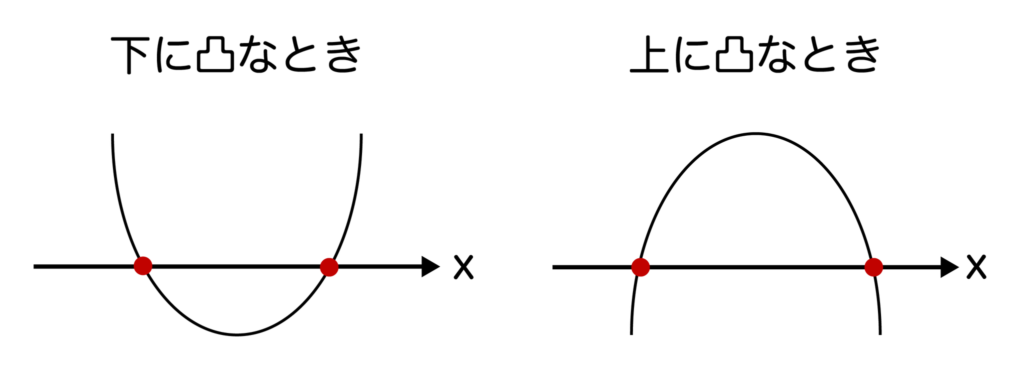
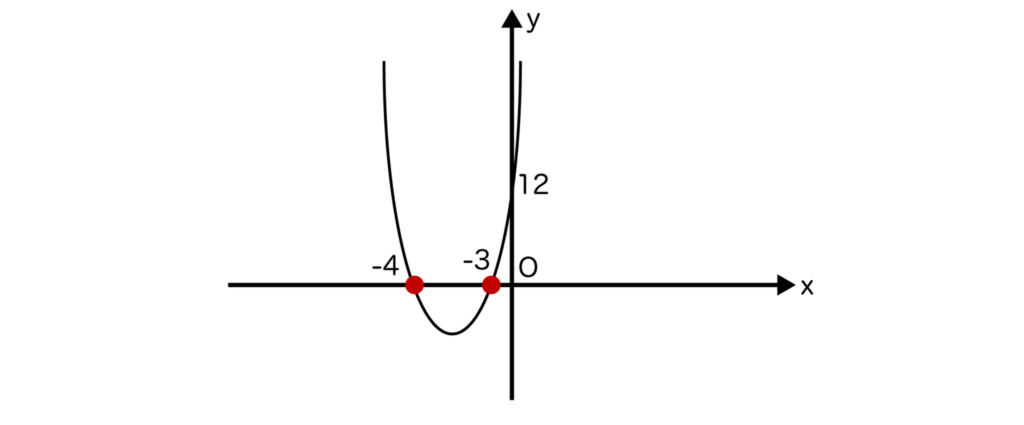
例えば、二次関数y=x²+7x+12を考えてみます。判別式D=7²-4×1×12=1>0より、二次関数y=x²+7x+12はx軸と異なる2点で交わります。

y=x²+7x+12を因数分解すると（x+3）（x+4）となるので、x=-4、-3となり、確かにx軸と異なる2点で交わることがわかります。

D=0 ⇔ 1点で接する

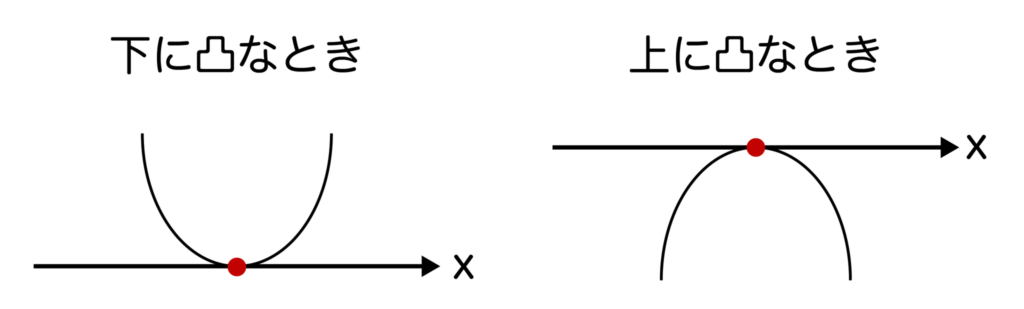
判別式D=b²-4ac=0のとき、y=ax²+bx+cはx軸と1点で接します。グラフで表現すると以下のようになります。

例えば、二次関数y=x²+4x+4を考えてみます。判別式D/4=2²-1×4=0より、二次関数y=x²+4x+4はx軸と異なる1点で交わります。

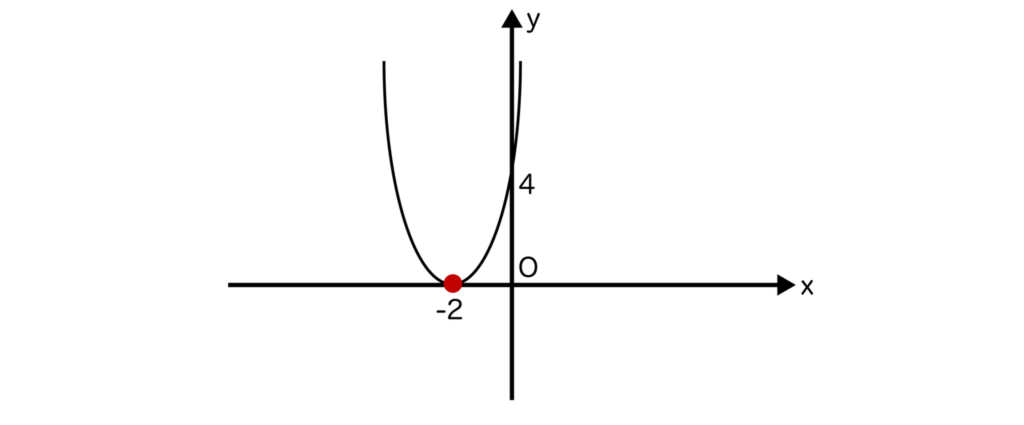
y=x²+4x+4を因数分解すると（x+2）²となるので、x軸との交点は以下のように1つのみとなります。

D<0 ⇔ 共通点なし

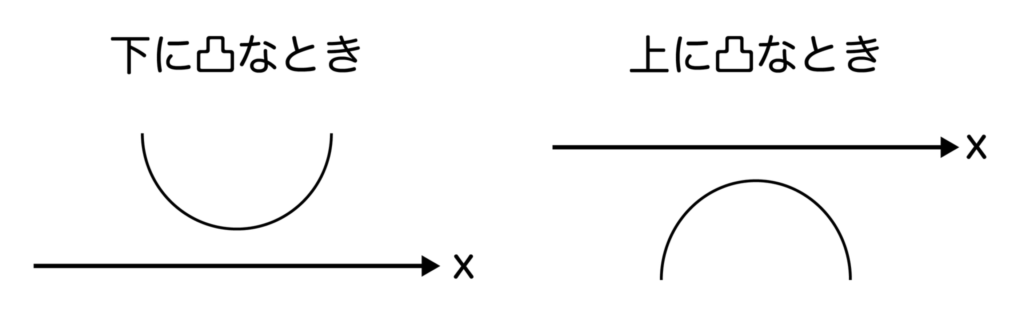
判別式D=b²-4ac<0のとき、y=ax²+bx+cはx軸と交わることはありません（＝共通点なし）

グラフで表現すると以下のようになります。

例えば、二次関数y=x²+4x+8を考えてみます。判別式D/4=2²-1×8=-4となるので、D<0よりy=x²+4x+8がx軸と交わることはありません。

x²+4x+8を平方完成すると（x+2）²+4となるので、頂点の座標は（-2、4）であることがわかり、グラフは以下のようになります。

※平方完成がわからない人は二次関数の平方完成の公式・やり方について解説した記事をご覧ください。

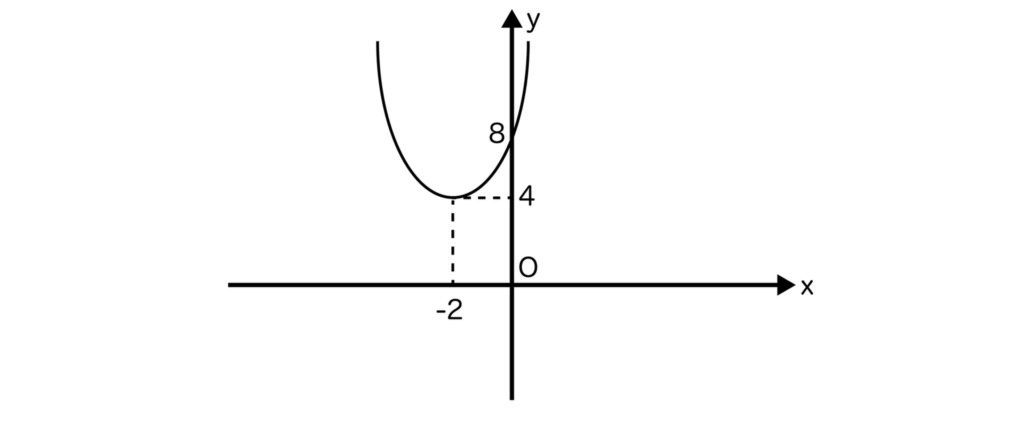
x軸との交点が1個もないことが確認できます。

判別式を使った練習問題

最後に、判別式を使った練習問題を解いてみましょう。すべて基本的な問題なので、全問正解できるまで内容を理解してください。

【練習問題1】

（1）二次方程式x²+7x+9=0の実数解の個数を求めよ。

（2）二次方程式x²+6x-2k+1=0の実数解の個数を求めよ。

（3）二次方程式x²+2mx+3m+10=0が重解を持つとき、mの値を求め、そのときの解も答えよ。

【解答＆解説】

（1）判別式D＝7²-4×1×9=13>0となるので、実数解の個数は2個・・・（答）となる。

（2）xの係数が6で偶数なので、D/4の判別式を使いましょう。

判別式D/4=3²-1×（-2k+1）=2k+8となりますね。よって、

• 2k+8>0のとき、すなわちk>-4のとき実数解は2個
• 2k+8=0のとき、すなわちk=-4のとき実数解は1個
• 2k+8<0のとき、すなわちk<-4のとき実数解は0個

となります。

（3）xの係数が2mで偶数なので、D/4の判別式を使います。

判別式D/4=m²-（3m+10）=m²-3m-10=（m+2）（m-5）となります。

判別式D/4=0のとき重解を持つので、m=-2、5となります。

m=-2のとき、二次方程式はx²-4x+4となり、x²-4x+4＝（x-2）²より重解＝2となります。

また、m=5のとき、二次方程式はx²+10x+25となり、x²+10x+25＝（x+5）²より重解＝-5となります。

【練習問題2】

二次関数y=x²-4x+kとx軸との交点の個数は、kの値によってどのように変わるか答えよ。

【解答＆解説】

xの係数が-4で偶数なので、D/4の判別式を使います。

判別式D/4=（-2）²-k=4-kです。よって、

• 4-k>0、つまりk<4のとき2個
• 4-k=0、つまりk=4のとき1個
• 4-k<0、つまりk>4のとき0個

となります。

いかがでしたでしょうか？今回は二次方程式の判別式とは何かについて解説した後、判別式はいつ使うのか？についても解説しました。

繰り返しにはなりますが、判別式は高校数学の中でも非常に重要な公式の1つです。解の公式と一緒に必ず覚えておきましょう。