高校数学の数学1における多項式の学習では「降べきの順・昇べきの順」が登場します。
内容はそこまで難しくないですが、2つの違いが覚えにくかったり、文字が2つ以上登場すると少し複雑になったりします。
そこで今回は、早稲田大学教育学部数学科を卒業した筆者が、降べきの順・昇べきの順に整理するやり方・覚え方について解説した後、文字が2つ以上ある場合やかっこでくくるケース、因数分解との関係についても解説します。
降べきの順・昇べきの順に整理するやり方と覚え方
まずは「降べきの順・昇べきの順に整理する」とは何かについて解説します。
降べきの順に整理するというのは、多項式において次数の高い項から順番に並べることです。
※多項式の項・次数とは何かについて解説した記事もご用意しているので、ぜひご覧ください。
例えば、5x+10x3-9x2+30という多項式があったとき、次数の高い項から順番に並べると、10x3-9x2+5x+30となりますね。
以上のように並び替えることを「降べきの順に整理する」というわけです。
逆に、昇べきの順に整理するというのは、多項式において次数の低い項から順番に並べることです。
先ほどご紹介した多項式を昇べきの順に整理すると、30+5x-9x2+10x3となります。
しかし、多項式を扱う場合は見やすさを考慮して一般的には降べきの順に整理することが多いです。
高校生の中には「どっちが降べきの順で、どっちが昇べきの順かわからなくなる」という人もいますが、覚え方は簡単です。
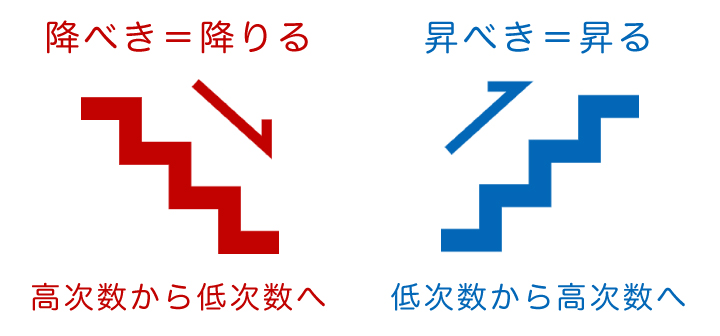
「降べき」の「降」は「降りる」という意味で、「昇べき」の「昇」は「昇る」という意味です。
降りる=高いところから低いところに移動する、昇る=低いところから高いところに移動するという意味なので、多項式に置き換えると、
- 降べきの順=高い次数から低い次数に降りていく
- 昇べきの順=低い次数から高い次数に昇っていく
となります。漢字の意味をしっかりと意識すれば簡単に覚えられるでしょう。
降べきの順・昇べきの順で文字が2つ以上ある場合
例えば、多項式a2x+4a3x+a+x+5のように文字が2つ以上ある場合(今回だとaとx)、どうやって降べきの順・昇べきの順に整理するか悩む人も多いと思います。
文字が2つ以上ある場合は、問題文にどの文字に注目すべきかが必ず記載してあります。
例えば、上記の多項式をaに注目して降べきの順・昇べきの順に整理することを考えてみます。
aに注目して降べきの順に整理するということは、aがたくさん掛け合わさっている項から順番に並べるということです。
よって、上記の多項式をaに注目して降べきの順に整理すると、4a3x+a2x+a+x+5となります。
※x+5は5+xでも問題ありません。
aに注目して昇べきの順に整理する場合は、aが掛け合わさっている数が少ない項から順番に並べるということです。
よって、上記の多項式をaに注目して昇べきの順に整理すると5+x+a+a2x+4a3xとなります。
※5+xはx+5でも問題ありません。
降べきの順・昇べきの順に整理するとき、かっこでくくるケースは?
降べきの順・昇べきの順に整理するとき、かっこ( )でくくることが推奨されているケースが2つあります。
1つ目は、同類項の整理です。
例えば、4x2+x3+ax+4+5xをxに注目して降べきの順に整理すると、x3+4x2+ax+5x+4となりますね。
※ax+5xは5x+axでも問題ありません。
以上でももちろん間違いではないのですが、ax+5xは(a+5)xとかっこでくくることができるので、x3+4x2+(a+5)x+4と記載した方が見やすくはなり、数学的には美しいとされています。
※多項式の計算方法について解説した記事もぜひ合わせてご覧ください。
2つ目は定数項をかっこでくくるケースがあります。
例えば、x+5x3+10x2+a+9をxに注目して降べきの順に整理すると5x3+10x2+x+a+9となりますね。
以上でももちろん間違いではありませんが、中には定数項であるa+9をかっこでくくって、5x3+10x2+x+(a+9)と表現する人もいます。
定数項をかっこでくくることにより、定数項であることをわかりやすくするためです。
しかし、上記でも解説した通り、かっこでくくるのは必須ではありませんし、くくらなくても減点されたりすることはないのでご安心ください。
数学の表現方法の1つとして覚えておく程度で問題ありません。
降べきの順と因数分解の関係
降べきの順は多項式を見やすくできるだけでなく、因数分解をするときにも役立つケースがあります。
難易度の高い因数分解の問題が出題されたとき、次数の低い文字に注目するというテクニックがあります。
例えば、a2-b2-3ac+3bcを因数分解してみます。
文字はa、b、cの3つがあり、もっとも次数が低いのはcなので、cに注目してについて降べきの順に整理してみます。
すると、
3(b-a)c+a2-b2
=3(b-a)c+(a+b)(a-b)
=-3(a-b)c+(a+b)(a-b)
=(a-b)(a+b-3c)・・・(答)
となります。高校数学の数学1では上記はまだ学習しませんが、降べきの順を用いた因数分解のテクニックは大学入試や共通テストでも頻出なので、学習が進んでいった際には必ず覚えておきましょう。
※数学1の因数分解について詳しく解説した記事もぜひ合わせてご覧ください。
降べきの順・昇べきの順の練習問題
最後に降べきの順・昇べきの順に関する練習問題をご用意しました。
すべて基礎的な問題なので、必ず解けるようにしておきましょう。
【練習問題1】
多項式5-3a2+2a-a3+a2+9a-1を降べきの順・昇べきの順に整理せよ。
【解答&解説】
項5と-1、-3a2とa2、2aと9aは整理できるので、まずはそれらを整理します。
5-3a2+2a-a3+a2+9a-1=-2a2+11a-a3+4となりますね。
よって、降べきの順に整理すると、-a3-2a2+11a+4・・・(答)となります。
昇べきの順に整理すると、4+11a-2a2-a3・・・(答)となります。
【練習問題2】
多項式x2+2xy-y2+3x+4y-10をxに注目して降べきの順・昇べきの順に整理せよ。
【解答&解説】
xに注目して降べきの順に整理すると、x2+(2y+3)x-y2+4y-10・・・(答)となります。
xに注目して昇べきの順に整理すると、-10+4y-y2+(2y+3)x+x2・・・(答)となります。
いかがでしたでしょうか?今回は降べきの順・昇べきの順に整理するやり方・覚え方について解説した後、文字が2つ以上ある場合やかっこでくくるケースや因数分解との関係もご紹介しました。
降べきの順・昇べきの順は高校数学の中でもかなり基礎的な用語の1つなので、必ずマスターしておきましょう。


