二等辺三角形の定義と定理（性質）を超わかりやすく解説！

「二等辺三角形の定義と定理（性質）を答えよ」と言われたら皆様は即座に回答できますでしょうか？

二等辺三角形の定義と定理（性質）は意外と忘れがちですが、図形の性質の基本事項でもあるので必ず覚えておきましょう。

本記事では早稲田大学教育学部数学科を卒業した筆者が二等辺三角形の定義と定理（性質）について図解でわかりやすく解説していきます。

数学や図形が苦手な生徒でも理解できるように解説していくので、ぜひ最後までお読みください。

二等辺三角形の定義

まずは二等辺三角形の定義からご紹介します。

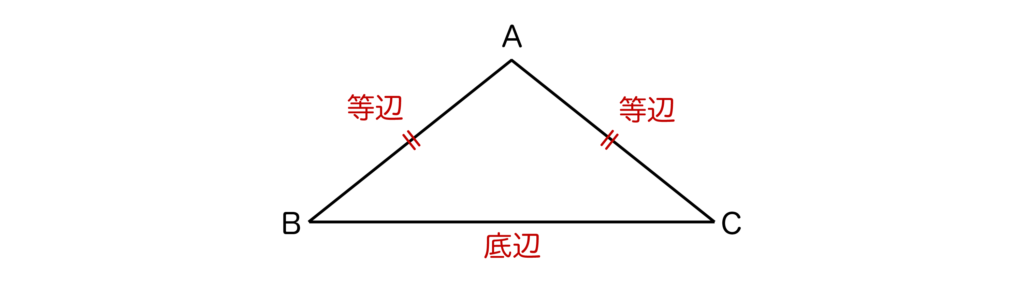
二等辺三角形とはその名の通り「2つの辺の長さが等しい三角形」のことです。

辺の長さが等しい2つの辺を等辺といい、残りの1つの辺を底辺というので覚えておきましょう。

ちなみにですが、底辺の長さが等辺と同じになる場合は三角形の3辺すべてが同じ長さということになるので、その三角形は正三角形となります。

二等辺三角形の定義が理解できたところで、ここからは二等辺三角形の定理（性質）を2つご紹介していきます。

まず1つ目は、AB＝ACの二等辺三角形ABCにおいては∠B＝∠Cが成り立つということです。

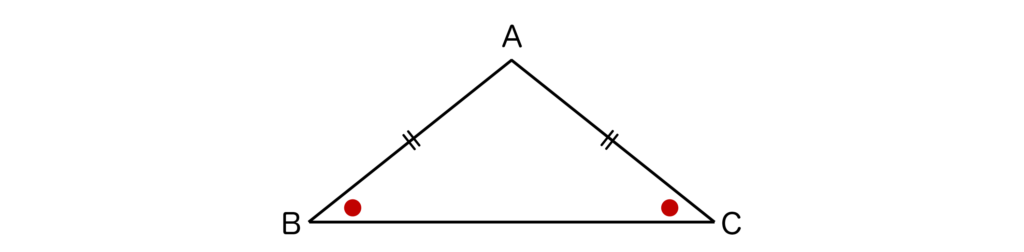
∠Aは頂角、∠Bと∠Cは底角と呼ばれているので覚えておきましょう。

二等辺三角形の定理（性質）2つ目は、AB＝ACの二等辺三角形ABCにおいて点AからBCに対して下ろした垂線とBCとの交点をDとすると、ADは底辺であるBCを垂直に二等分するということです。

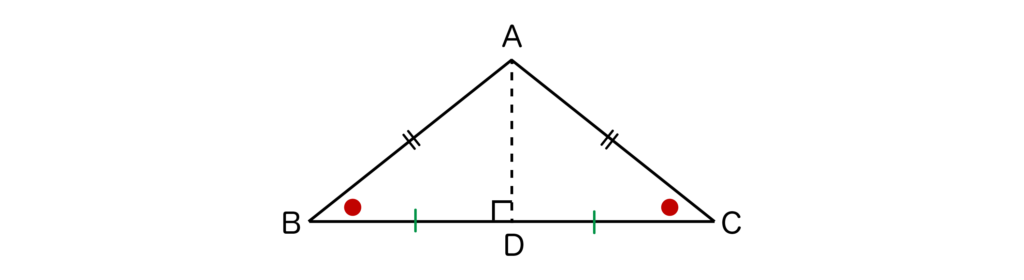
つまり、BD＝CDとなります。

以上2つが二等辺三角形の定理（性質）となります。特に2つ目の定理（性質）は忘れがちなので、しっかりと頭に入れておきましょう。

ちなみにですが、ある三角形ABCが与えられたとき、その三角形ABCがAB＝ACの二等辺三角形であることを証明するには、

という3つの方法があります。

二等辺三角形の定義と定理（性質）も重要ですが、二等辺三角形になるための条件も非常に重要なので合わせて覚えておきましょう。

二等辺三角形の一種として直角二等辺三角形があります。

直角二等辺三角形は直角三角形の定理（性質）と上記でご紹介した二等辺三角形の定理（性質）の両方を合わせて持っています。

というわけでここからは、直角三角形の定理（性質）3つを簡単にご紹介しておきます。

まず1つ目の定理（性質）は、直角を除く他の2つの角の和は直角（＝90°）であるということです。

以下の直角三角形ABCにおいて∠Cが直角である場合、残りの角の和（∠A＋∠B）は90°になるということです。

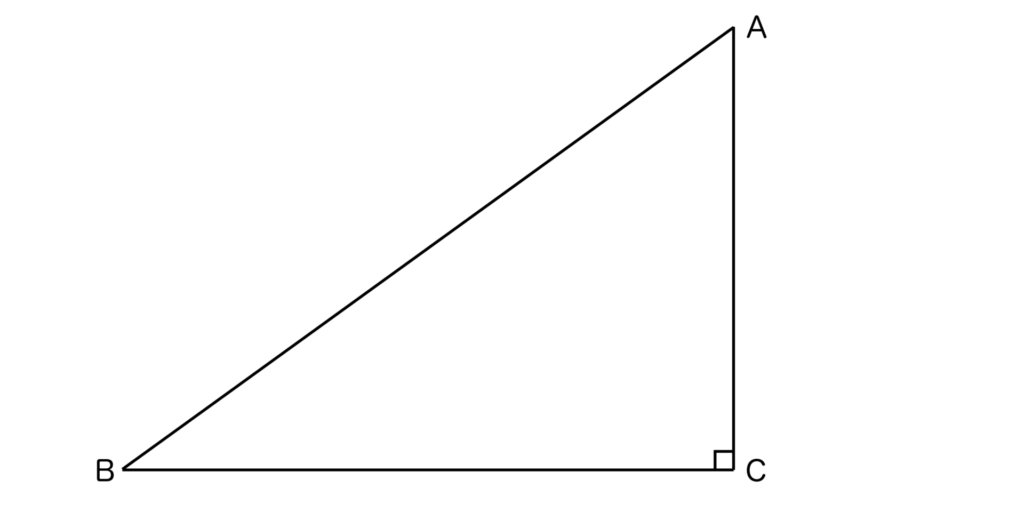
三角形の内角の和は180°ですので、∠A＋∠B＋∠C＝180°となります。

∠C＝90°なので、∠A＋∠B＝180°-90°＝90°となることが証明できます。

※三角形の内角の和が180°になる理由がわからない人は内角・外角とは何かについて解説した記事をご覧ください。

直角三角形の定理（性質）2つ目は、斜辺の中点は3頂点から等距離にあるということです。

以下の直角三角形ABCにおいて斜辺であるABの中点をDとすると、AD＝DB＝DCが成り立ちます。

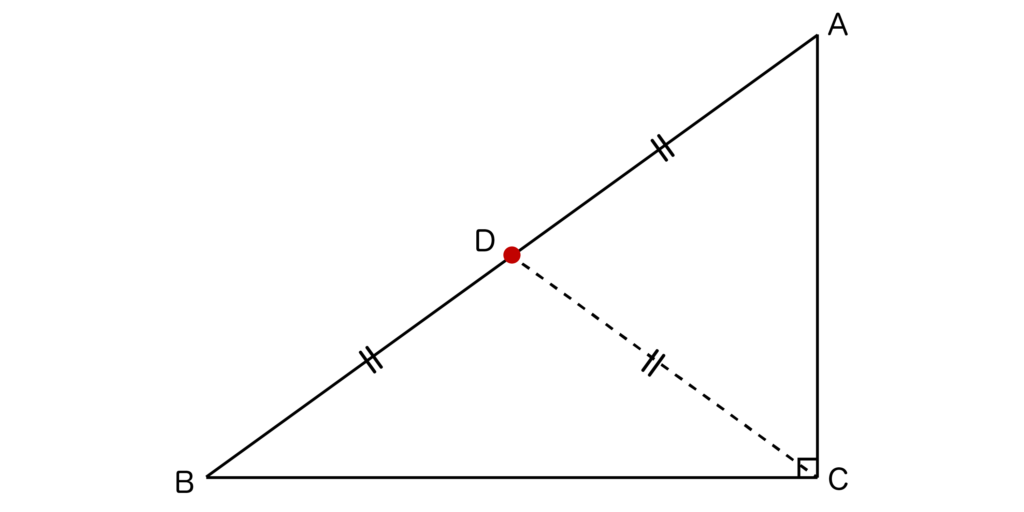
以上の定理（性質）が成り立つことの証明ですが、∠ACB＝90°であることから、辺ABを直径とした円を描いたとき、その円周上に点Cが存在することになります。

この円の中心は点Dなので、AD＝DB＝DC（すべて円の半径）が成り立ちます。

直角三角形の定理（性質）3つ目は、斜辺の平方（＝2乗）は残りの2辺の平方の和に等しいということです。これは俗にいう三平方の定理（ピタゴラスの定理）です。

以下の直角三角形ABCにおいて、AB²＝AC²＋BC²が成り立ちます。

以上が直角三角形の定理（性質）となります。直角二等辺三角形は以上3つの定理（性質）に加えて、二等辺三角形の定理（性質）2つも合わせ持つということを理解しておきましょう。

いかがでしたか？

今回は二等辺三角形の定義と定理（性質）を図解で解説していきました。

二等辺三角形に関する知識は数学の図形問題を解く上では必須です。二等辺三角形の定義や定理（性質）を忘れてしまったときはぜひ本記事を見返してください。