相関係数は高校数学の数学1の「データの分析」のおいて最も計算力が要求される値です。
後ほど詳しく解説しますが、相関係数を求めることで2変量データの間に成り立つ関係を客観的に分析できるようになります。
本記事では早稲田大学教育学部数学科を卒業した筆者が相関係数とは何かについて解説した後、相関係数の求め方・公式をご紹介します。
また、相関係数の目安や相関係数を求めるための裏ワザもご紹介していきますので、ぜひ最後までご覧ください。
相関係数とは?
2変量データの間に相関関係があるかどうかを調べるためには散布図(相関図)を書けば良いのでした。
※詳しくは散布図の書き方や見方について解説した記事をご覧ください。
散布図の見た目から相関の正負や強弱を判断することももちろん可能ですが、場合によっては見た目では判断が難しいときもあります。
また、見た目だけの判断では人によって判断にばらつきが出てしまう可能性もあります。
そんな課題を解決するため、客観的な指標として相関関係の正負や強弱を判断することができる「相関係数」という指標が用意されています。
相関係数の求め方・公式を例題で解説
ここからは、例題をもとにして相関係数を実際に求めていきます。
相関係数を求めるためにはいくつかの手順を踏まなければならないので、1つ1つしっかり理解していきましょう。
【例題】
あるクラスで5人の生徒を対象に数学と化学のテスト(ともに10点満点)が行われた。数学のテストの点数をx、化学のテストの点数をyとしたとき、以下のデータを得ることができた。このとき、xとyの相関係数rを求めなさい。
| 数学の点数x[点] | 1 | 0 | 3 | 5 | 1 |
| 化学の点数y[点] | 3 | 3 | 4 | 9 | 1 |
【解答&解説】
相関係数を求める手順は以下の7ステップとなります。
- 平均値を求める
- 各データから平均値を引く(偏差を求める)
- 偏差平方を求める
- 偏差積を求める
- 標準偏差を求める
- 共分散を求める
- 相関係数を求める
それぞれ順番に計算していきましょう。
平均値を求める
まずはxとyの平均値を求めましょう。
| 数学の点数x[点] | 1 | 0 | 3 | 5 | 1 |
| 化学の点数y[点] | 3 | 3 | 4 | 9 | 1 |
xの平均=(1+0+3+5+1)/5=2
yの平均=(3+3+4+9+1)/5=4
ですね。
※度数分布表の平均値の求め方について解説した記事もご用意しているので、ぜひ合わせてご覧ください。
各データから平均値を引く(偏差を求める)
次は各データから平均値を引いた値を求めていきます。すると、以下のようになりますね。
| x | y | x-xの平均 | y-yの平均 |
|---|---|---|---|
| 1 | 3 | 1-2=-1 | 3-4=-1 |
| 0 | 3 | 0-2=-2 | 3-4=-1 |
| 3 | 4 | 3-2=1 | 4-4=0 |
| 5 | 9 | 5-2=3 | 9-4=5 |
| 1 | 1 | 1-2=-1 | 1-4=-3 |
ちなみに、各データから平均値を引いた値のことを偏差と呼ぶのでした。
※詳しくは標準偏差とは何かについて解説した記事をご覧ください。
偏差平方を求める
続いては偏差平方を求めます。偏差平方とは偏差の2乗のことでした。
偏差平方を求めると、以下のようになりますね。
| x | y | x-xの平均 | y-yの平均 | (x-xの平均)の2乗(偏差平方) | (y-yの平均)の2乗(偏差平方) |
|---|---|---|---|---|---|
| 1 | 3 | 1-2=-1 | 3-4=-1 | 1 | 1 |
| 0 | 3 | 0-2=-2 | 3-4=-1 | 4 | 1 |
| 3 | 4 | 3-2=1 | 4-4=0 | 1 | 0 |
| 5 | 9 | 5-2=3 | 9-4=5 | 9 | 25 |
| 1 | 1 | 1-2=-1 | 1-4=-3 | 1 | 9 |
偏差積を求める
偏差平方を求めたら、次は偏差積を求めます。
偏差積とは(x-xの平均)と(y-yの平均)の積(=掛け算)のことです。偏差積を求めると以下のようになります。
| x | y | x-xの平均 | y-yの平均 | (x-xの平均)の2乗(偏差平方) | (y-yの平均)の2乗(偏差平方) | 偏差積 |
|---|---|---|---|---|---|---|
| 1 | 3 | 1-2=-1 | 3-4=-1 | 1 | 1 | (-1)×(-1)=1 |
| 0 | 3 | 0-2=-2 | 3-4=-1 | 4 | 1 | (-2)×(-1)=2 |
| 3 | 4 | 3-2=1 | 4-4=0 | 1 | 0 | 1×0=0 |
| 5 | 9 | 5-2=3 | 9-4=5 | 9 | 25 | 3×5=15 |
| 1 | 1 | 1-2=-1 | 1-4=-3 | 1 | 9 | (-1)×(-3)=3 |
標準偏差を求める
ここまで来たら、次は標準偏差を求めます。
標準偏差は分散の正の平方根でした。
※詳しくは分散とは何かについて解説した記事をご覧ください。
分散は偏差平方の平均なので、
- xの分散=(1+4+1+9+1)/5=16/5
- yの分散=(1+1+0+25+9)/5=36/5
となります。
したがって、
- xの標準偏差=4/√5
- yの標準偏差=6/√5
となります。
共分散を求める
続いては共分散を求めます。初めて共分散という言葉を聞いた人もいるでしょう。
共分散とは偏差積の平均のことです。
つまり、共分散=(1+2+0+15+3)/5=21/5となります。
共分散という言葉は数学1「データの分析」でも重要用語の1つなので、必ず覚えておきましょう。
相関係数を求める
ここまで来たらあと一歩です。
相関係数を求めるには標準偏差と共分散の2つが必要です。
相関係数=共分散 / (xの標準偏差)×(yの標準偏差)で求めることができます。
つまり、相関係数=21/5 ÷ (4/√5 × 6/√5)=21/5 ÷ 24/5=7/8・・・(答)となります。
少数に直すと7÷8=0.875です。
以上が相関係数の求め方となります。相関係数=共分散 / (xの標準偏差)×(yの標準偏差)という公式は必ず覚えておきましょう。
※相関係数はかなり奥が深く、なぜ上記でご紹介した計算方法で相関係数が求められるのか?については高校数学で取り扱うことはできませんので割愛させていただきます。
相関係数の目安とは?
相関係数rは-1≦r≦1になることが知られています。
そして、rの値が1に近いほど正の相関が強くなり、-1に近いほど負の相関が強くなります。
また、rの値が0に近いほど相関は弱くなります。
以上をまとめると以下のようになります。
- r=-1のとき、完全な負の相関関係
- r=-0.9(一例)のとき(-1に近いとき)、強い負の相関関係
- r=-0.3(一例)のとき、負の相関関係
- r=0のとき、相関関係はない
- r=0.3(一例)のとき、正の相関関係
- r=0.9(一例)のとき(1に近いとき)、強い正の相関関係
- r=1のとき、完全な正の相関関係
※相関係数の求め方のときと同様に、なぜ上記のような相関係数の目安が成り立つのか?については高校数学で取り扱うことはできませんので割愛させていただきます。
相関係数を求める裏ワザ
上記の例題で相関係数を求めたとき、最終的には以下の計算式が登場しました。
相関係数=21/5 ÷ (4/√5 × 6/√5)=21/5 ÷ 24/5=7/8
以上の式における計算では、分母・分子にある5が消えますが、この5は標準偏差や共分散を求めるときに5で割ったことによって登場した数字です。
しかし、この5は消えてしまうので、標準偏差や共分散を計算するときの「5で割る」という作業は不要だとわかります。
以上より、相関係数=偏差積の和 / √(xの偏差平方の和) × √(yの偏差平方の和)で求めることも可能となります。
少しだけ計算が楽になる裏ワザとなりますので、覚えておくと便利です。
以上の裏ワザで上記の例題における相関係数を計算してみると、
相関係数
=(1+2+0+15+3)/ √(1+4+1+9+1) × √(1+1+0+25+9)
=21/√16 × √36
=7/8
となり、確かにもとの21/5 ÷ (4/√5 × 6/√5)の結果と同じになっていることが確認できます。
相関係数の注意点
相関係数は非常に便利な指標ですが、相関係数から安易に傾向が分析できないケースもあるので注意が必要です。
本記事では2つのケースについてご紹介していきます。
外れ値が含まれる場合
相関係数は外れ値の影響を受けやすいという弱点があります。
例えば、以下の散布図では相関が見られませんが、右上に外れ値があることが原因で相関関係は1に近い数値となります。
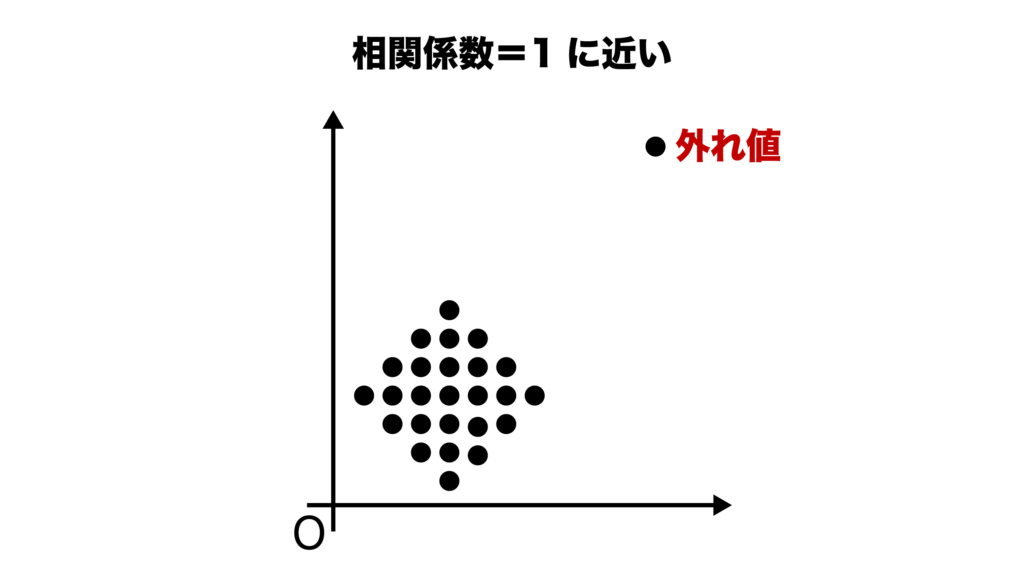
しかし、この右上の外れ値を外した場合、相関係数は0になり、散布図の状態と相関係数の値とが一致します。
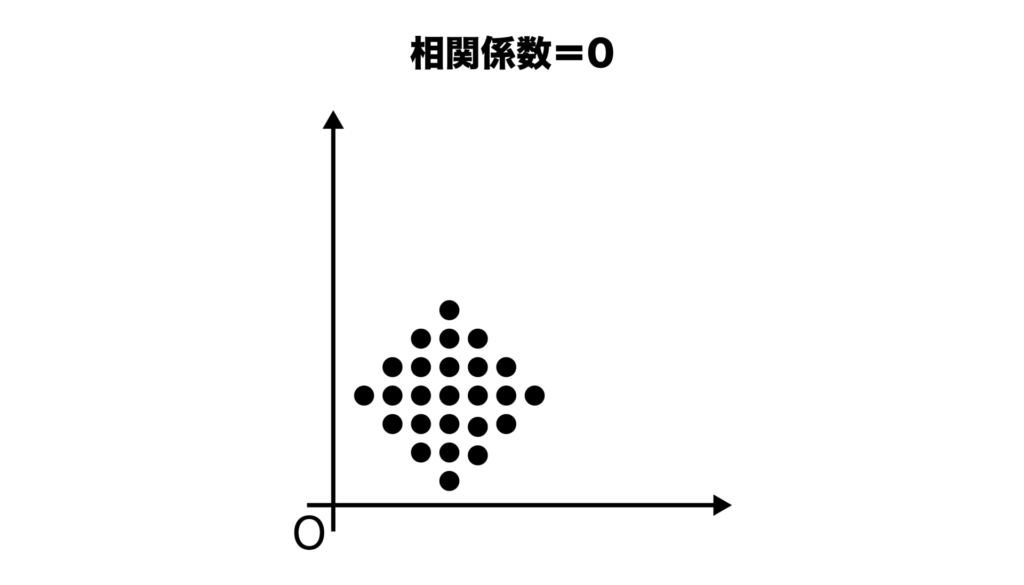
相関係数は平均値と同じで、外れ値の影響を受けやすいということを覚えておきましょう。
相関係数を用いてデータの分析を行う際には、データの中に外れ値が含まれていないかの確認が必要です。
偽相関の場合
偽相関という言葉があるので覚えておきましょう。偽相関とは見かけ上、相関関係が発生していることです。
有名な例としては都道府県別の建物出火件数と乗用車保有台数の相関関係があります。
実際に上記の相関係数を計算すると、相関係数=約0.88となることが確認できており、強い正の相関関係があるといえます。
つまり、建物出火件数が多い都道府県は乗用車の保有台数も多いということです。
しかし、都道府県によって人口は大きく異なり、人口の多い・少ないが建物出火件数と乗用車の保有台数に影響を与えている可能性が高いと考えられます。
乗用車の保有台数が多い=人口が多いと考えられ、その結果として建物の件数も多くなるから出火も多くなると考えられるのです。
以上のように、建物出火件数と乗用車保有台数の間に共通の別の変量(今回の場合は人口)が関係して、見かけ上は相関関係が発生しているケースがあるのです。
※実際に、都道府県の人口格差をなくすために、人口千人あたりの乗用車保有台数と建物出火件数の相関係数を調べてみると、相関係数=約0.02となり、相関関係がないことが確認されています。
以上の話は散布図の書き方や見方について解説した記事で取り上げている相関関係と因果関係の話に近いものとなります。相関関係・因果関係・偽相関は3つセットでぜひ覚えておきましょう。
いかがでしたか?
今回は相関係数とは何かや相関係数の求め方・公式について解説していきました。
相関係数の目安や裏ワザも非常に便利で、大学入試や共通テストでも必ず役に立つので、ぜひ覚えておいてください。


