高校数学の数学1で学習する「命題と証明」では対偶・逆・裏という用語が登場します。
数学1の中でも非常に重要な用語の1つであり、大学入試や共通テストでもよく出題されるので、必ず覚えておきましょう。
そこで今回は、早稲田大学教育学部数学科を卒業した筆者が対偶とは何かについてわかりやすく解説します。また、対偶が成り立つことの証明や逆・裏とは何かなども合わせて解説します。
本記事を読めば数学苦手な人でも対偶・逆・裏が理解できると思います。ぜひ最後までお読みください。
対偶・逆・裏とは?わかりやすく解説
まずは対偶・逆・裏とは何かについてわかりやすく解説していきます。
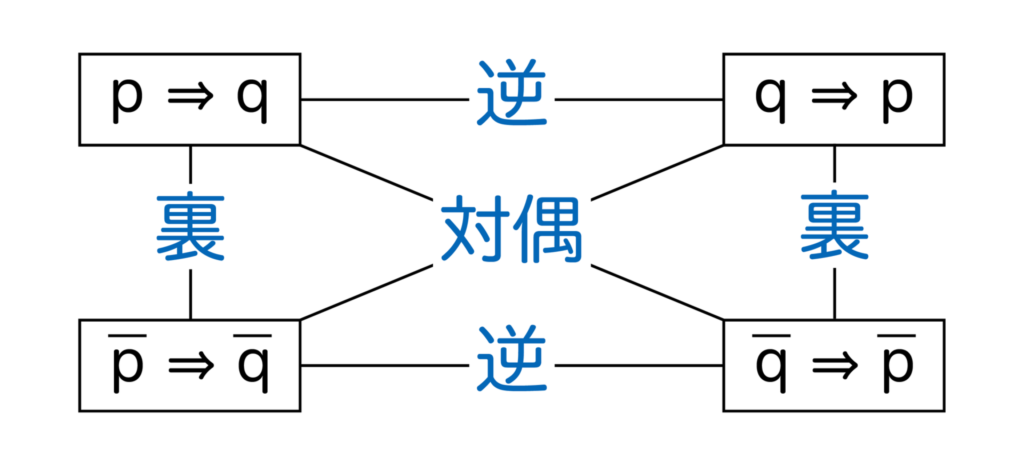
命題p⇒qがあるとします。
※命題が何かわからない人は、命題とは何かについて解説した記事をご覧ください。
このとき、
q⇒pを逆、q⇒pを対偶、p⇒qを裏と言います。
図にまとめると以下のようになります。
言葉だけだとわかりにくいと思うので、例で考えてみましょう。
命題「x=3⇒x2=9」の逆・対偶・裏を考えてみます。
※「x=3⇒x2=9」は明らかに真ですね。
逆はq⇒pのことなので、「x2=9⇒x=3」となります。真偽の確認もしておきましょう。
9の平方根は3と-3なので、逆の命題は偽となります。
※平方根の求め方がわからな人は、平方根とは何かについて解説した記事をご覧ください。
対偶はq⇒pのことなので、「x2≠9⇒x≠3」となります。x2≠9ということはx≠3、x≠-3なので、この命題は真となります。
そして、裏はp⇒qのことなので「x≠3⇒x2≠9」となります。x=-3のときでもx2=9となるので、これは偽となります。
以上を見てもおわかりかと思いますが、命題の真偽とその対偶の真偽は一致します。
また、命題の裏は逆の対偶なので、逆と裏の真偽も必ず一致します。
以上は非常に重要なので、絶対に覚えておきましょう。
対偶の証明(命題と真偽と一致)
先ほども解説した通り、命題の真偽と対偶の真偽は必ず一致します。ここからは、その証明を行います。
条件、p、qを満たすもの全体の集合をそれぞれP、Qとします。
※集合がわからない人は、集合について解説した記事をご覧ください。
p⇒qが真
⇔ P⊂Q
⇔ Q⊂P
⇔ 対偶q⇒pが真
となります。
逆と裏の真偽が一致することの証明は先ほども解説した通り、命題の裏は逆の対偶なので、逆と裏の真偽も必ず一致することになります。
なので、命題p⇒qが与えられたとき、p⇒qを証明する代わりにその対偶q⇒pを証明しても問題ありません。
対偶・逆・裏の練習問題
対偶・逆・裏の意味が理解できたところで、対偶・逆・裏に関する練習問題を解いてみましょう。
【練習問題】
以下の命題の逆・対偶・裏を述べて、その真偽を判定しなさい。a、bは実数とする。
※実数がわからない人は、実数とは何かについて解説した記事をご覧ください。
(1)4の倍数は2の倍数である。
(2)a+b>0ならば、a>0かつb>0である。
【解答&解説】
(1)逆は「2の倍数は4の倍数である。」となります。
これは偽となります。判例としては、2があげられます(2は2の倍数ですが、4の倍数ではありません)
対偶は「2の倍数でないなら、4の倍数でない。」となります。
これはもとの命題「4の倍数は2の倍数である。」が明らかに真なので、対偶も真となります。
裏は「4の倍数でないなら、2の倍数でない。」となります。逆が偽なので、裏も偽となります。
(2)逆は「a>0かつb>0ならば、a+b>0である。」となります。
これは明らかに成り立つので真となります。
対偶は「a≦0またはb≦0ならば、a+b≦0である。」となります。
※「かつ」の否定は「または」となります。詳しくは必要条件・十分条件について解説した記事をご覧ください。
これは偽となります。反例としては、a=-2、b=5があげられます。「a≦0またはb≦0」なので、aとbどちらかが0以下であれば問題ありません。
※「≦」の意味がわからない人は、不等号の意味と読み方について解説した記事をご覧ください。
裏は「a+b≦0ならば、a≦0またはb≦0である。」となります。
逆が真なので、裏も真となります。
対偶を利用した証明問題
上記でも解説した通り、命題の真偽とその対偶の真偽は一致します。
そのことを用いた証明問題は共通テストでも頻出なので、慣れておきましょう。
【問題】
nを整数としたとき、n2が3の倍数ならば、nは3の倍数であることを証明しなさい。
【解答&解説】
「n2が3の倍数ならば、nは3の倍数である」の対偶は「nが3の倍数でないならば、n2は3の倍数ではない」となりますね。
対偶を証明できればもとの命題も証明できたことになるので、対偶の証明を行います。
nが3の倍数でないとき、kを整数としてn=3k+1またはn=3k+2と表すことができます。
[1]n=3k+1のとき、n2=(3k+1)2=3(3k2+2k)+1となるので、n2は3の倍数ではないことがわかります。
※2乗の計算方法がわからない人は、数学1の因数分解について解説した記事をご覧ください。
[2]n=3k+2のとき、n2=(3k+2)2=3(3k2+4k+1)+1となるので、n2は3の倍数ではないことがわかります。
[1]と[2]より、対偶が真であることが証明されたので、もとの命題も真となります。
対偶を利用して証明をするかどうかの見極めポイント
先ほど対偶を利用して命題を証明する方法をご紹介しましたが、このテクニックを使うべきかどうかはどうやって見極めれば良いのでしょうか?
結論としては、命題の結論に注目すると良いです。
特に、結論が以下のようになっている場合は対偶を利用した証明ができないか?を考えてみましょう。
- 「〇〇または××」「少なくとも1つは〇〇」「〇〇かつ××」
- 「〇〇ではない」「〇≠×」「〇〇である」
※対偶を利用した証明と背理法による証明は合わせて間接証明法と呼ばれています。背理法とは何かについて解説した記事もぜひ参考にしてください。
今回は対偶・逆・裏とは何かについて解説した後、対偶が成り立つことの証明や練習問題をご紹介しました。
命題と対偶の真偽、逆と裏の真偽は一致することは非常に重要なので、必ず覚えておきましょう。