高校数学の数学Aにおける場合の数では円順列が登場しますが、円順列を苦手とする人は多いのではないでしょうか?
円順列は公式が用意されているものの、いざ問題を解くとなれば公式を使うだけでは解けないケースが多いので難しく感じる人が多いのかもしれません。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が円順列の公式をご紹介した後、なぜ公式で-1が発生するのか?や円順列において「向かい合う」「隣り合わない」などの頻出パターンも解説していきます。
円順列とは?公式はなぜ-1が必要なのか
いくつかのものを円形に並べる配列を円順列といいます。
※順列の意味がわからない人は順列とは何かについて解説した記事をご覧ください。
円順列では、円を回転させて並びが一致するものは同じものと考えます。
例えば以下のようにA、B、C、D、Eを円形に並べたとき、以下の2つは回転させると一致するので同じものとみなします。
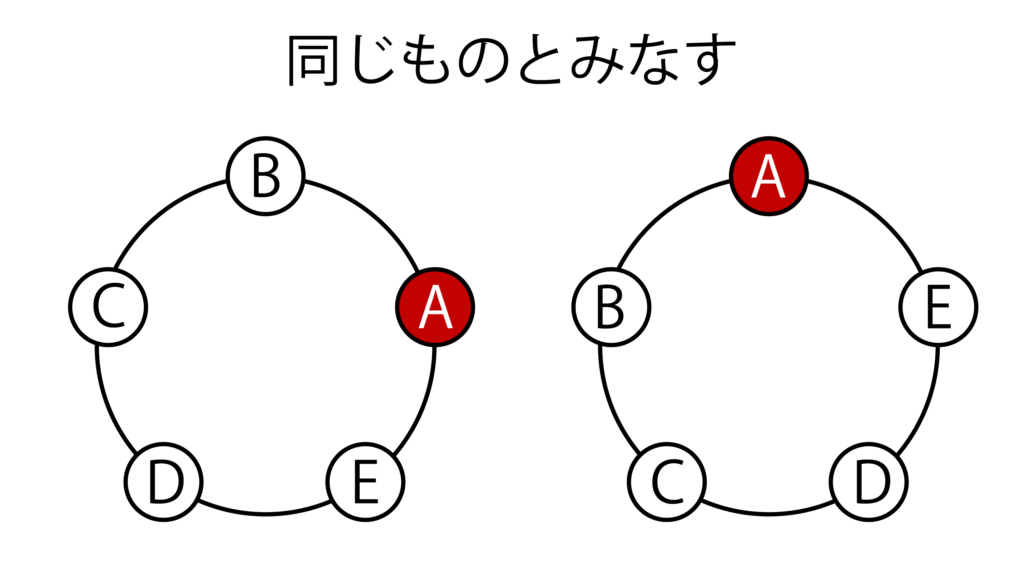
以上の図の右側の円において、一番上のAを起点にして反時計回りにアルファベットを表記するとABCDEとなりますね。
同様に考えると以上の図の左側の円はBCDEAとなります。
他のパターンとしては、
- CDEAB
- DEABC
- EABCD
がありますね。以上の5つは円順列としてすべては同じものとみなされます。
1つの円順列に対して5つの順列があり、順列の総数は5P5なので、求める円順列の総数をxとすると、x・5=5P5が成り立ちます。
よって、x=5P5 / 5=5!/5=(5-1)![通り]となります。
これはまた、1つのもの、例えばAを固定して、他のB〜Eの4つを並べると考えることもできるので、4P4=(5-1)!=4![通り]としても求めることが可能です。
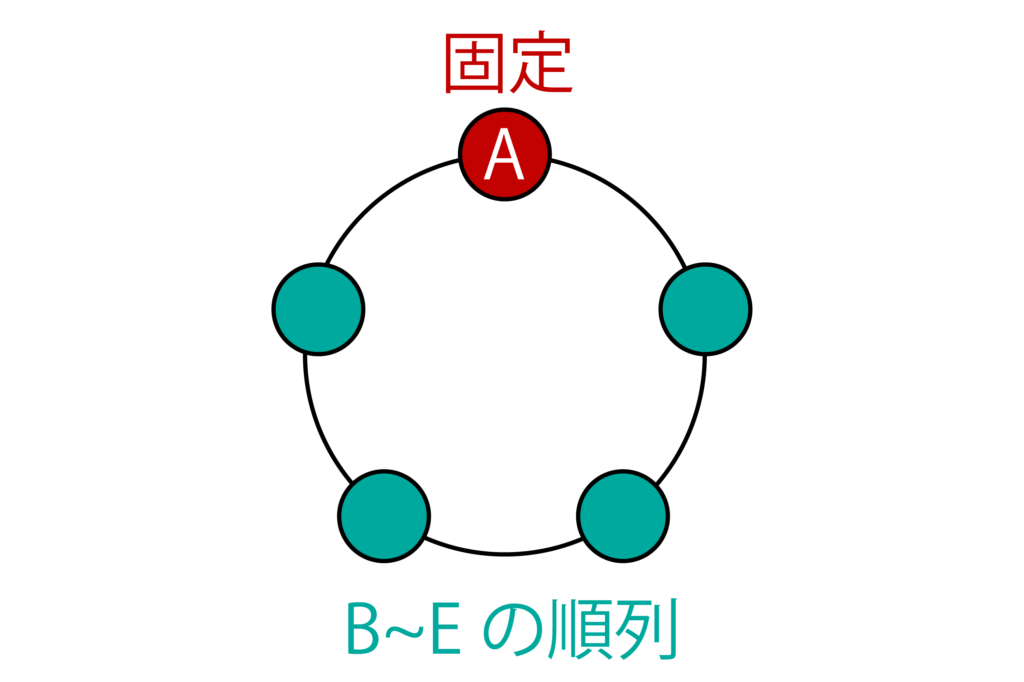
異なるn個のものについても同様に考えることができるので、円順列の総数を求める公式は
nPn / n=n-1Pn-1=(n-1)!
となります。
円順列の公式(n-1)!は必ず覚えておきましょう。
円順列の基礎問題
以上の円順列の公式を踏まえて、円順列の基礎問題を解いてみましょう。
【問題】
異なる6個の石がある。このとき、以下の問いに答えよ。
(1)これらの石を円形に並べる方法は全部で何通りあるか求めよ。
(2)6個の石から4個を取り出し、円形に並べる方法は全部で何通りあるか求めよ。
【解答&解説】
(1)円順列の公式より、(6-1)!=5!=5・4・3・2・1=120[通り]・・・(答)
(2)異なる6個の石から4個を取り出す順列6P4には、円順列としては同じものが4通りずつ存在するので、6P4 / 4 =90[通り]・・・(答)となります。
円順列の向かい合う・隣り合う・隣り合わないに関する問題
円順列の問題では
- 向かい合う
- 隣り合う
- 隣り合わない
という言葉がよく登場しますのでしっかり対策をしておきましょう。
【問題】
6個の数字1、2、3、4、5、6を円形に並べる。このとき、以下の問いに答えよ。
(1)1と2が向かい合う並べ方は何通りあるか求めよ。
(2)1と2が隣り合う並べ方は何通りあるか求めよ。
(3)1と2が隣り合わない並べ方は何通りあるか求めよ。
【解答&解説】
(1)1を固定して考えてみましょう。すると、2は1の向かい合う位置に決定しますね。
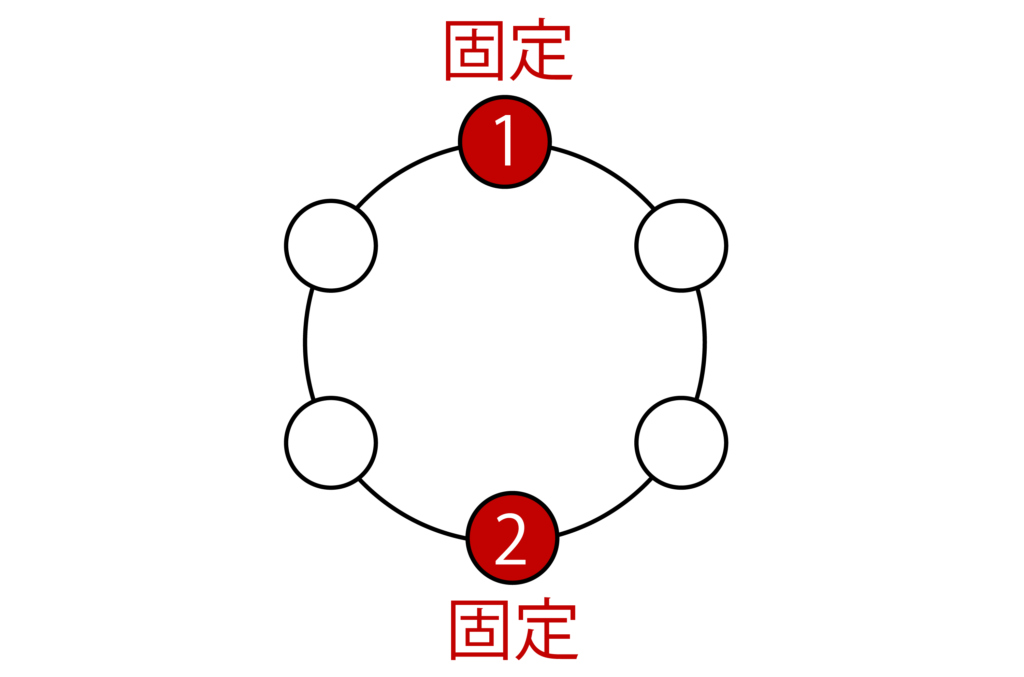
残りの4つの位置に3、4、5、6を並べれば良いので、答えは4!=24[通り]・・・(答)となります。
(2)「隣り合う」を考えるときは、隣り合うものを1組と考えるのが定石です。
今回は1と2を1組と考えてみましょう。
この1組と残りの3、4、5、6を円形に並べる方法は、円順列の公式より(5-1)!=24[通り]ですね。
1と2の並べ方は2!=2[通り]です。
よって、24・2=48[通り]・・・(答)となります。
(3)1と2が隣り合わない並べ方=すべての並べ方 – 1と2が隣り合う並べ方ですね。
すべての並べ方は円順列の公式より(6-1)!=5!=120[通り]
1と2が隣り合う並べ方は(2)より48[通り]
よって答えは120-48=72[通り]・・・(答)となります。
円順列において「隣り合わない」という言葉が登場したときは、全体から隣り合う場合を引いた方が楽に解けるケースが多いので、ぜひ覚えておいてください。
円順列を活用した塗り分けの問題
最後に円順列を活用した塗り分けの問題をご紹介します。
【問題】
立方体の各面に、隣り合った面の色は異なるように色を塗る。このとき、異なる6色すべてを使って塗る方法は何通りあるか求めよ。
ただし、立方体を回転させて一致する塗り方はすべて同じものとみなす。
【解答&解説】
「回転させて一致するものはすべて同じとみなす」とするときは、特定のものを固定して他のものの配列を考えると解きやすいです。
今回の場合、上面に1つの色を固定してみましょう。そして、残りの5面の塗り方を考えます。
このとき、下面の色は残りの色で塗るので5通りありますね。
そのおのおのについて側面の塗り方は異なる4色の円順列となるので、(4-1)!=6[通り]となります。
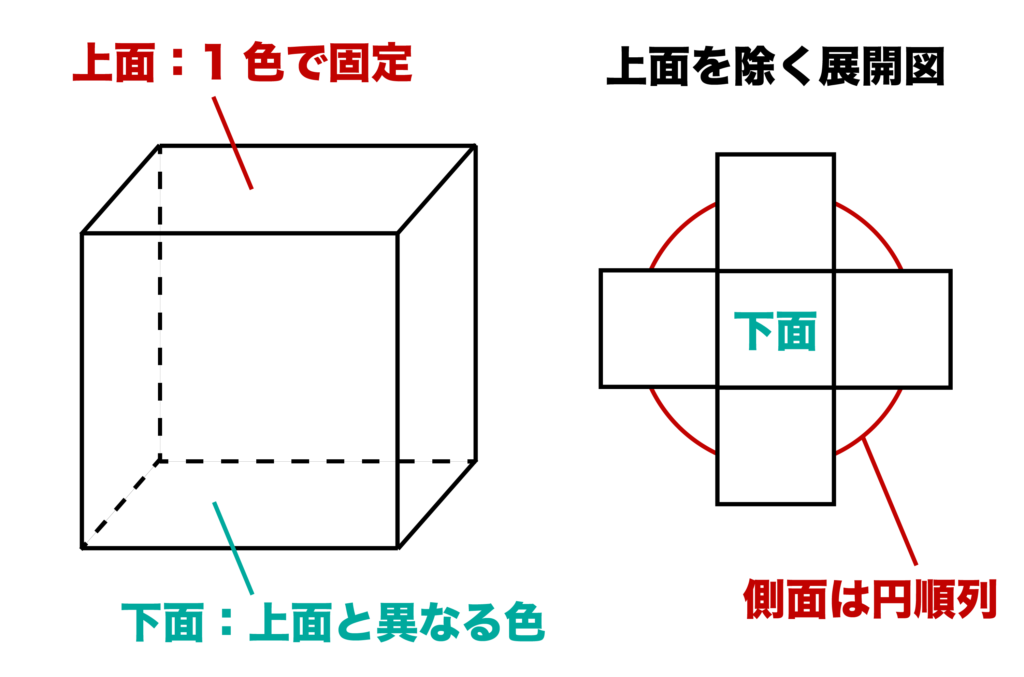
よって5・6=30[通り]・・・(答)となります。
円順列と数珠順列
円順列と似たような順列として数珠順列があります。数珠は「じゅず」と読みます。
数珠順列とは首飾りのように、異なるいくつかのものを円形に並べ、回転または裏返して一致するものは同じものとみなすときの並び方のことをいいます。
問題文に首飾りやネックレス、腕輪、ブレスレットなど裏返すことができるものが登場したら数珠順列を疑いましょう。
異なるn個のものの数珠順列の総数=(n-1)! / 2となります。
詳しくは数珠順列について解説した記事をご覧ください。
いかがでしたでしょうか?
今回は円順列の公式と公式においてなぜ-1が登場するのかについて解説した後、向かい合う・隣合わないなどの言葉が登場する円順列の問題をご紹介していきました。
円順列は解き方が思いつきにくいジャンルの1つなので、ぜひたくさんの問題を解いて感覚を養っていってください。


