ある三角形が二等辺三角形であることを証明するには3つの方法があります。
すべて基本的なことなのですが、意外と忘れがちなのでぜひこの機会に二等辺三角形になるための条件を学習しておきましょう。
本記事では二等辺三角形になるための条件3つと証明について早稲田大学教育学部数学科を卒業した筆者が図解でわかりやすく解説していきます。
最後には二等辺三角形であることを証明する練習問題もご用意しているので、ぜひ最後までご覧ください。
二等辺三角形になるための条件1つ目
ある三角形が二等辺三角形になるための条件1つ目は「2つの辺が等しい」ことです。これは二等辺三角形の定義でもあります。
※二等辺三角形の定義と定理(性質)について解説した記事もぜひ合わせてご覧ください。
例えば、以下の三角形ABCにおいて、AB=ACであることを証明できれば三角形ABCはAB=ACの二等辺三角形であると言えます。
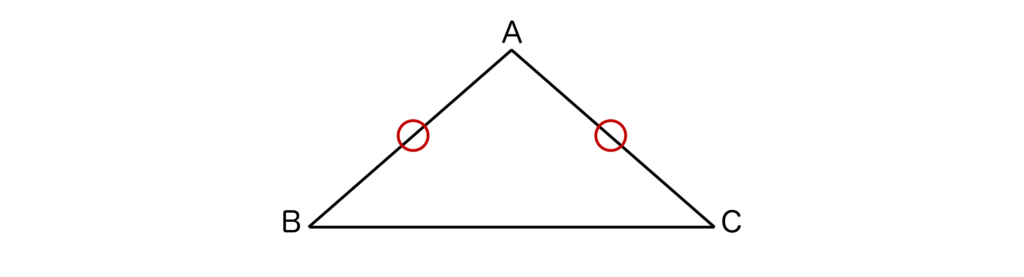
このとき、二等辺三角形の性質より∠B=∠Cとなります。
二等辺三角形になるための条件2つ目
二等辺三角形になるための条件2つ目は「2つの角が等しい」ことです。
これも非常にシンプルです。
例えば、以下の三角形ABCにおいて、∠B=∠Cであることを証明できれば三角形ABCはAB=ACの二等辺三角形であると言えます。
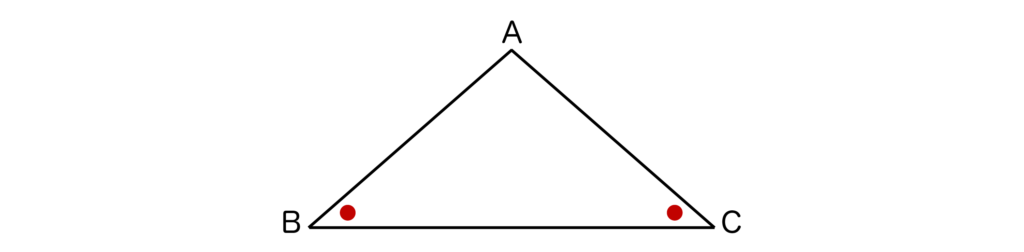
※二等辺三角形辺の角度の求め方について解説した記事もぜひ合わせてご覧ください。
二等辺三角形になるための条件3つ目
いよいよ最後です。二等辺三角形になるための条件3つ目は「頂角の二等分線が底辺の垂直二等分線と一致する」ことです。
これは意外と忘れがちな条件なのでしっかりと頭に入れておきましょう。
※二等辺三角形の底辺の長さの求め方について詳しく解説した記事もぜひ合わせてご覧ください。
例えば、以下の三角形ABCにおいて、∠Aの二等分線ADを引いたとき、ADがBCの垂直二等分線になっていることを証明できれば三角形ABCはAB=ACの二等辺三角形であると言えます。
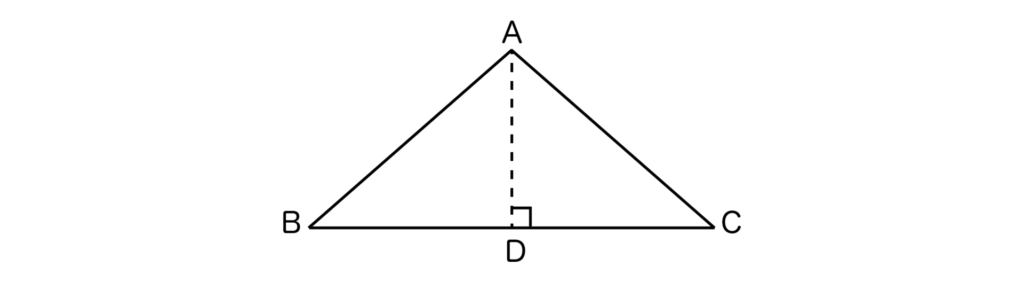
また、三角形ABCが二等辺三角形であることから∠B=∠Cも成り立ちます。
※二等辺三角形の頂角から垂線を下ろして三平方の定理を使い、辺の長さを求めるという方法はよく使います。詳しくは二等辺三角形と三平方の定理の関係について解説した記事をご覧ください。
二等辺三角形になるための条件を活用した証明問題
以上で解説した二等辺三角形になるための条件を理解した上で、ここからはその条件を活用した証明問題を解いてみましょう。
【問題1】
以下の二等辺三角形ABCにおいて、∠ABCの二等分線と∠ACBの二等分線の交点をDとする。このとき、三角形DBCは二等辺三角形となることを証明せよ。
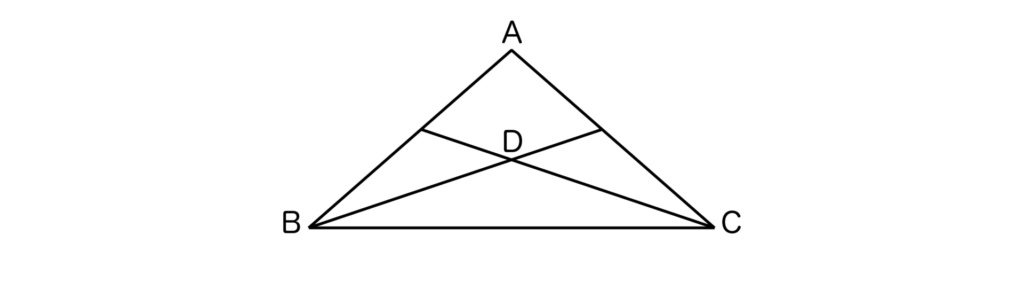
【解答&解説】
三角形ABCは二等辺三角形であることから、∠ABC=∠ACBが成り立ちます。
∠ABCの二等分線と∠ACBの二等分線の交点がDであることから、∠DBC=∠DCBとなることがわかります。
よって、2つの角が等しいので、三角形DBCは二等辺三角形であることが証明できます(二等辺三角形になるための条件2つ目)
【証明終】
以上は非常に基本的な証明問題となります。必ず解けるようにしておきましょう。
【問題2】
以下の二等辺三角形ABCにおいて、点BからACに対して引いた垂線とACとの交点をD、点CからABに対して引いた垂線とABとの交点をEとする。
また、BDとCEの交点をFとする。このとき、三角形FBCは二等辺三角形となることを証明せよ。
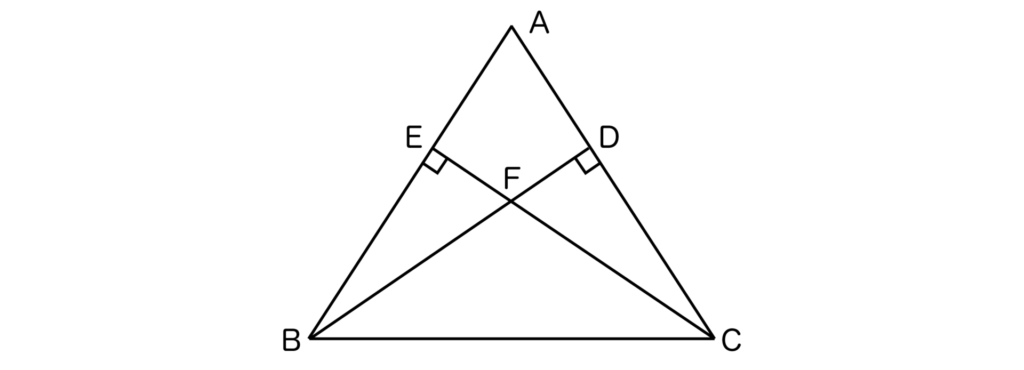
【解答&解説】
三角形BDCと三角形CEBに注目します。三角形ABCは二等辺三角形であることから、
∠DCB=∠EBC・・・①が成り立ちます。また、
- BCは共通・・・②
- ∠BDC=∠CEB=90°・・・③
ですね。よって、①・②・③より斜辺と1つの鋭角がそれぞれ等しい(直角三角形の合同条件)ので、三角形BDCと三角形CEBは合同になります。
※三角形と直角三角形の合同条件について解説した記事もぜひご覧ください。
よって、∠DBC=∠ECBとなり、2つの角が等しいので、三角形FBCは二等辺三角形であることが証明できます(二等辺三角形になるための条件2つ目)
【証明終】
いかがでしたか?
今回は二等辺三角形になるための条件3つと証明問題を2つご紹介しました。
特に二等辺三角形になるための条件3つ目である「頂角の二等分線が底辺の垂直二等分線と一致する」は非常に忘れやすいので、しっかりと頭に入れておきましょう。