二等辺三角形の底辺の長さの求め方はしっかりと理解できていますでしょうか?
二等辺三角形の底辺の長さを求めると、その二等辺三角形の面積を求められたりします。
図形問題を解く上では二等辺三角形の底辺の長さは必ず自力で求められるようにしておかなければなりません。
本記事では早稲田大学教育学部数学科を卒業した筆者が二等辺三角形の底辺の長さについて図解でわかりやすく解説していきます。
数学や図形問題が苦手な人でも理解できるように解説していくので、ぜひ最後までご覧ください。
二等辺三角形の底辺の長さの求め方
基本的に、二等辺三角形の底辺の長さを求めるには頂角を挟む2辺の長さと高さの2つが必要です。
例えば以下の図のようにAB=AC=15、AD=10の二等辺三角形の底辺の長さBCを求めてみましょう。
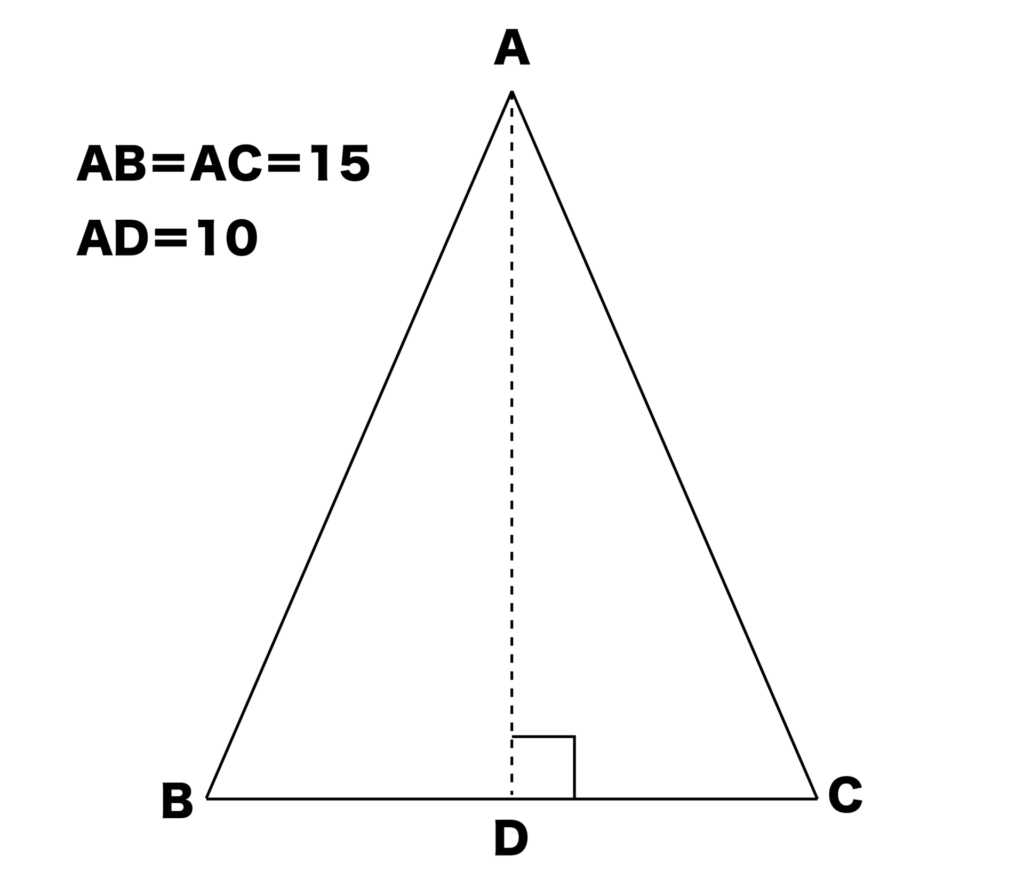
三角形ABDに注目し、三平方の定理を使います。
AB2=AD2+BD2より、152=102+BD2となるので、
BD2=225-100=25となります。
BD>0より、BD=5となります。
※BD=5になる理由がわからない人は平方根とは何かについて解説した記事をご覧ください。
ここで、ADはBCの垂直二等分線になるのでした。
※詳しくは二等辺三角形の定義と定理(性質)について解説した記事をご覧ください。
つまり、底辺BC=2×BD=10となります。
以上が基本的な二等辺三角形の底辺の長さの求め方となります。
二等辺三角形と三平方の定理の組み合わせは非常によく使うので、必ず使いこなせるようにしておきましょう。
二等辺三角形と三平方の定理の関係について解説した記事もご用意しているので、ぜひ参考にしてください。
頂角=120°の二等辺三角形の底辺の長さの求め方
頂角=120°の二等辺三角形の場合は1つの辺の長さがわかっていれば底辺の長さを求めることができます。
頂角=120°の二等辺三角形の辺の比は決まっています。以下の図の∠A=120°の二等辺三角形ABCにおいて、AB:AC:BC=1:1:√3になります。
※詳しくは二等辺三角形と比の関係について解説した記事をご覧ください。

なので、例えば以上の三角形ABDにおいてAB=20だとすると、BC=AB×√3=20√3になります。
では、以下の図のように高さADだけわかっている頂角=120°の二等辺三角形ABCの底辺の長さはどうでしょうか?AD=30として底辺BCを求めてみます。
※二等辺三角形の高さの求め方について解説した記事もぜひ参考にしてください。
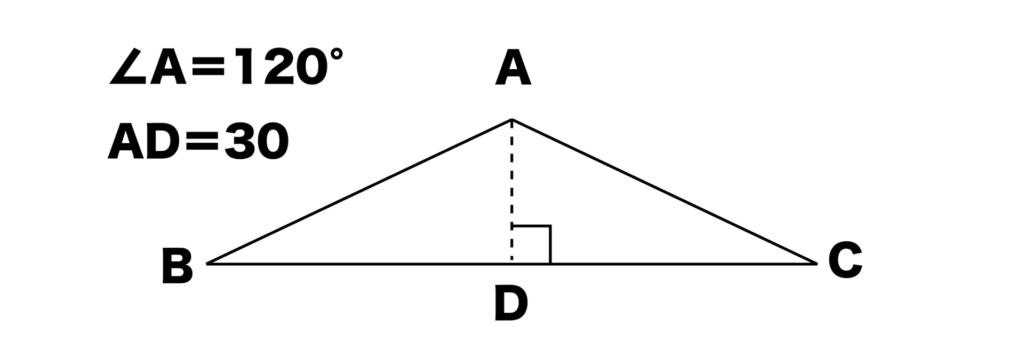
ADはBCの垂直二等分線かつ∠Aの二等分線でもあるので、∠BAD=60°となります。
すると、三角形ABDは60°型の直角三角形なので、AD:BD=1:√3であることがわかります。
よって、BD=30×√3=30√3となります。したがって、底辺BC=2×30√3=60√3となります。
ちなみにですが、AD:AB=1:2なのでAB=30×2=60です。
AB:AC:BC=60:60:60√3となり、確かに1:1:√3になっていることがわかります。
頂角=30°の二等辺三角形の底辺の長さの求め方
頂角=30°の二等辺三角形の底辺の長さも、先ほど解説した頂角=120°の二等辺三角形と同様に1つの辺の長さがわかっていれば底辺の長さを求めることができます。
以下の図のように∠A=30°の二等辺三角形ABCは辺の比AB:AC:BC=(√2+√6):(√2+√6):2となります。
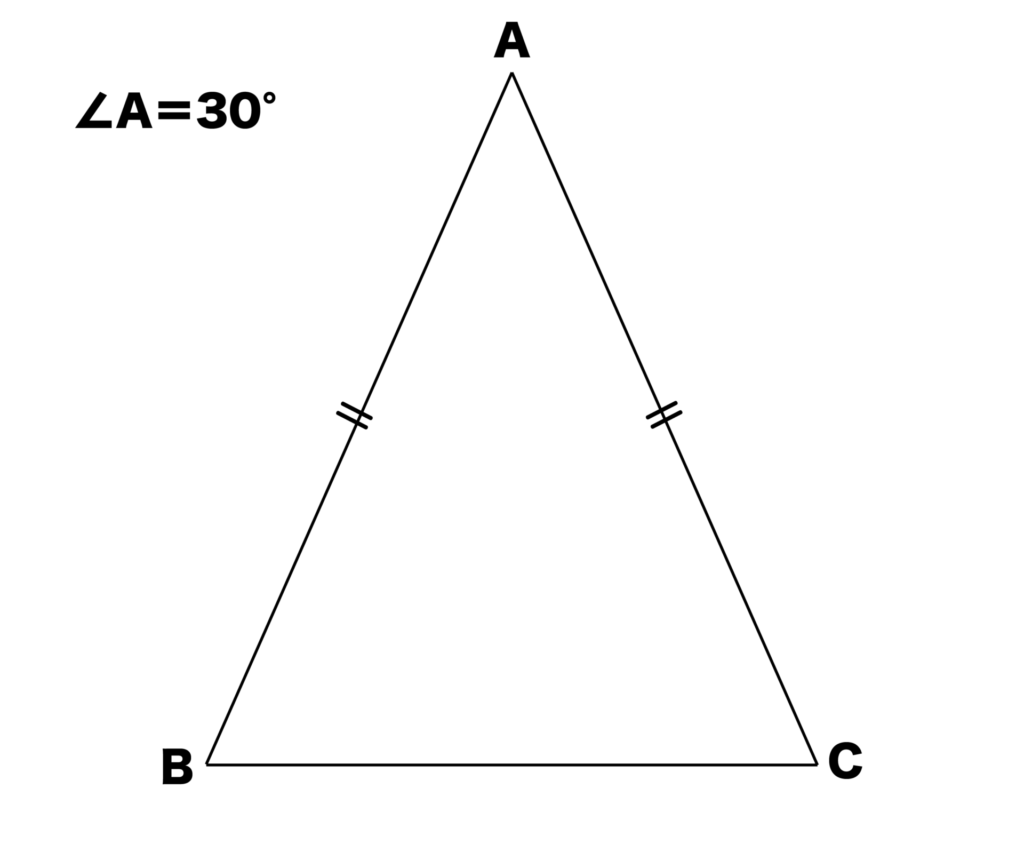
なので、例えば上記の頂角=30°の二等辺三角形ABCにおいて、AB=10とすると、底辺BCの長さ=10×2/(√2+√6)=5√6-5√2となります。
では、頂角=30°の二等辺三角形ABCにおいて高さだけがわかっている場合はどうでしょうか?
以下の図のように二等辺三角形ABCにおいて、高さAD=18として、底辺BCを求めてみましょう。
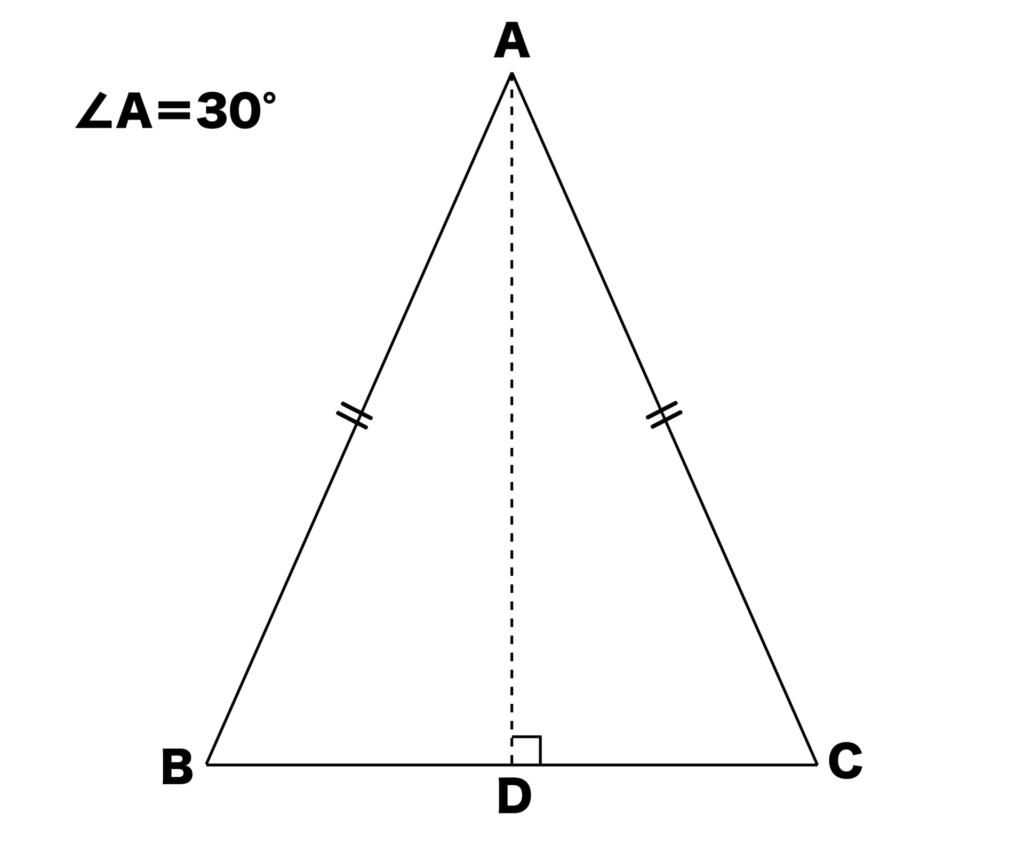
∠BADは∠Aの二等分線なので、15°となります。
15°型の直角三角形の辺の比はBD:AD:AB=1:(2+√3):(√2+√6)です。
※15°型の直角三角形の辺の比は応用的な内容のため取り上げていない教科書が多いですが、難関学校を目指す人は必ず覚えておきましょう。
よって、BD=AD×1/(2+√3)=181/(2+√3)=36-18√3となります。
BC=2×BD=2×36-18√3=72-36√3となります。
頂角=120°と30°の二等辺三角形は例外として1辺の長さだけわかれば底辺の長さを求めることができるということは必ず頭に入れておきましょう。
直角二等辺三角形の底辺の長さの求め方
直角二等辺三角形の底辺の長さの求め方はとても簡単です。
直角二等辺三角形の辺の比は以下の図のように1:1:√2になるのでした。
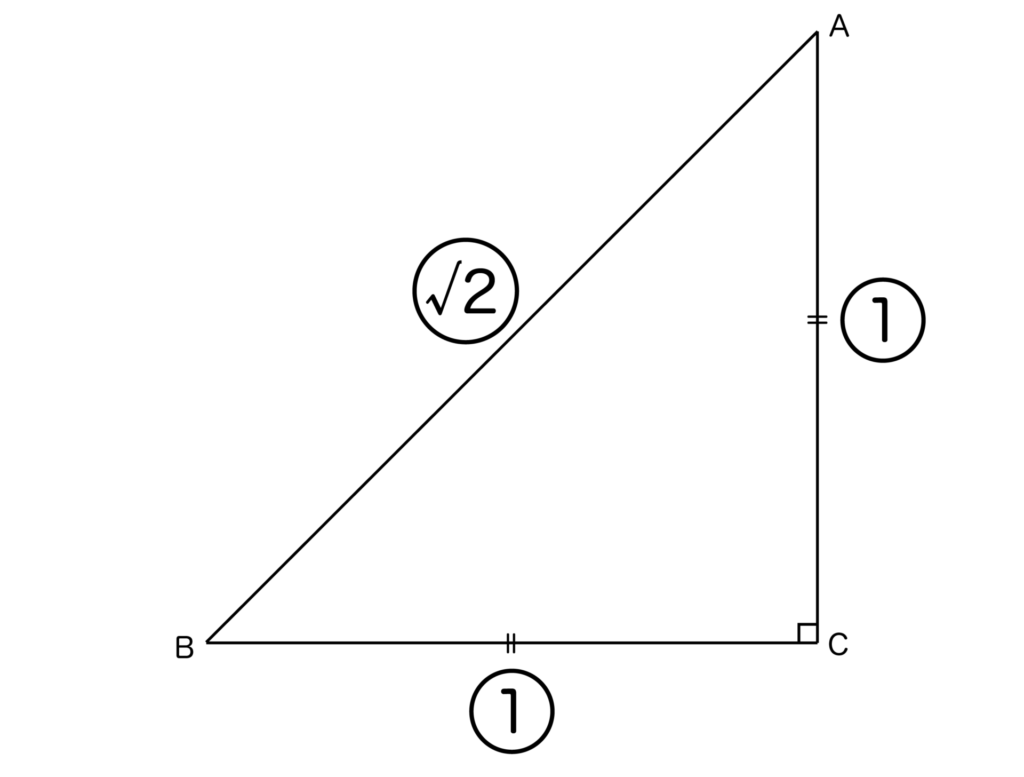
直角二等辺三角形の場合、頂角=∠C(=90°)とした場合、底辺はABになります。
よって、例えば上記の直角二等辺三角形ABCにおいてAC=AB=5の場合、底辺AB=5×√2=5√2となります。
直角二等辺三角形の辺の比は暗記必須なので、必ず覚えてください。
なぜ1:1:√2になるのか気になる人は直角二等辺三角形の辺の長さについて解説した記事をご覧ください。
いかがでしたか?
今回は二等辺三角形の底辺の長さの求め方について解説していきました。
頂角から底辺に対して垂線をおろすという手法は非常に重要ですので、必ず使いこなせるようにしておきましょう。