二等辺三角形辺の角度のを求める能力は数学の図形問題を解く上で必ず持っておかなければなりません。
そして、二等辺三角形辺の角度の求め方は非常に簡単なのでご安心ください。1分もあれば十分求めることができます。
本記事では早稲田大学教育学部数学科を卒業した筆者が二等辺三角形辺の角度の求め方について図解で解説していきます。
数学や図形問題が苦手な人でも理解できるようにわかりやすく解説するので、ぜひ最後までお読みください。
二等辺三角形辺の角度の求め方(頂角がわかっている場合)
まずは二等辺三角形において頂角がわかっている場合の底角の角度の求め方について解説します。
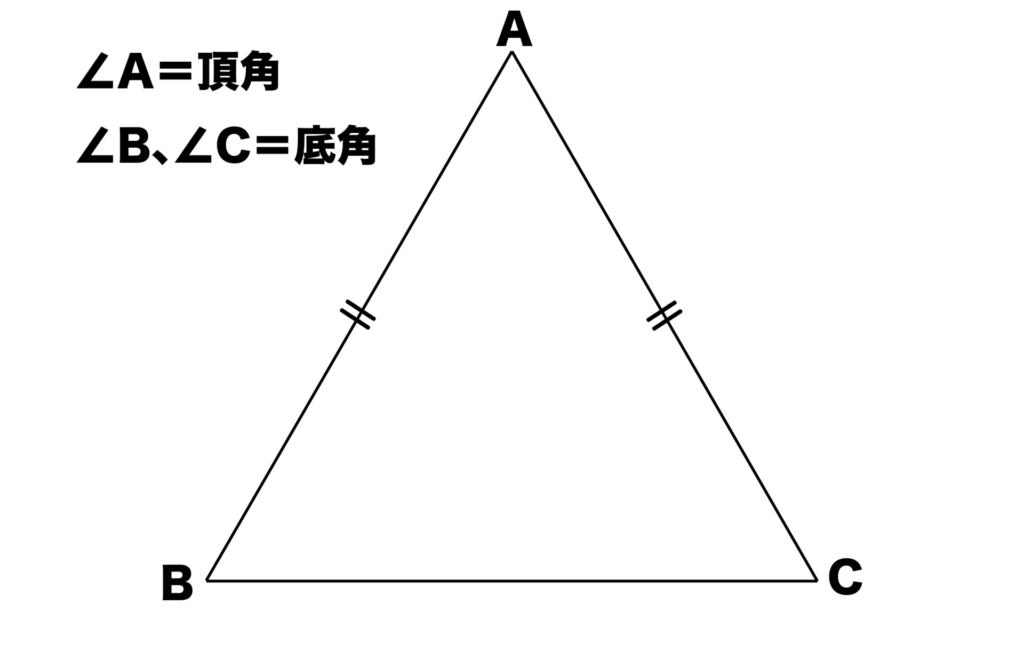
※二等辺三角形における頂角とは長さが等しい2辺に挟まれた角のことです。底角とは頂角を除く2つの角のことです。詳しくは二等辺三角形の定義と定理(性質)について解説した記事をご覧ください。
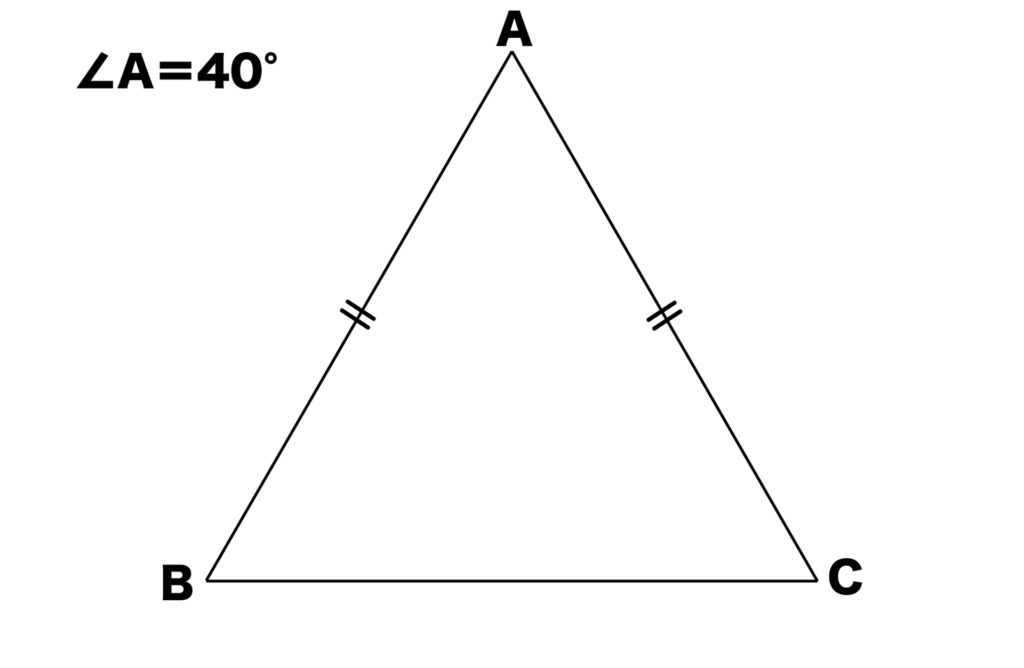
では、以下の図のように頂角である∠A=40°の二等辺三角形の∠Bと∠Cの大きさを求めてみましょう。
二等辺三角形においては2つの底角の大きさは等しいのでした。
つまり、∠B=∠Cとなります。
ここで、三角形の内角の和は180°でしたね。
※詳しくは内角・外角とは何かについて解説した記事をご覧ください。
つまり、∠A+∠B+∠C=180°が成り立ちます。ここで、∠A=40°なので、
∠B+∠C=140°
となります。上記の通り、∠B=∠Cなので、∠B=∠C=70°となります。
二等辺三角形では頂角の大きさがわかれば底角の大きさは必ず求まります。
二等辺三角形辺の角度の求め方(底角がわかっている場合)
次は二等辺三角形において底角がわかっている場合の頂角の角度の求め方について解説します。
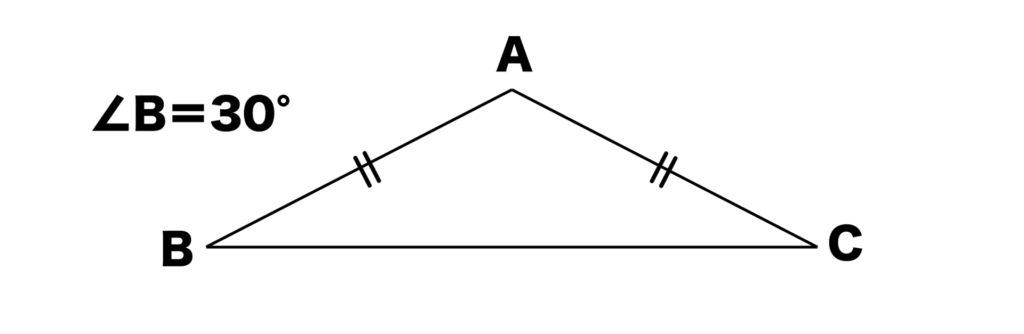
以下の図のように底角である∠B=30°の二等辺三角形の頂角∠Aの大きさを求めてみましょう。
先ほども解説した通り、二等辺三角形における2つの底角の大きさは等しいです。
よって、∠B=∠C=30°となります。
三角形の内角の和は180°なので、
∠A=180°-(∠B+∠C)=180°-60°=120°となります。
二等辺三角形においては底角の大きさがわかっていれば頂角の大きさも必ず求まります。
二等辺三角形辺の角度の超重要事項
二等辺三角形の頂角から底辺に対しておろした垂線は頂角の二等分線となります。また、底辺の垂直二等分線にもなります。
※二等辺三角形の底辺の長さの求め方について解説した記事もぜひ合わせてご覧ください。
これは二等辺三角形辺の角度の性質として非常に重要なので必ず覚えておきましょう。
例えば、以下の図のように頂角である点Aから底辺であるBCに対しておろした垂線ADは∠Aの二等分線になります。また、ADはBCの垂直二等分線にもなります。
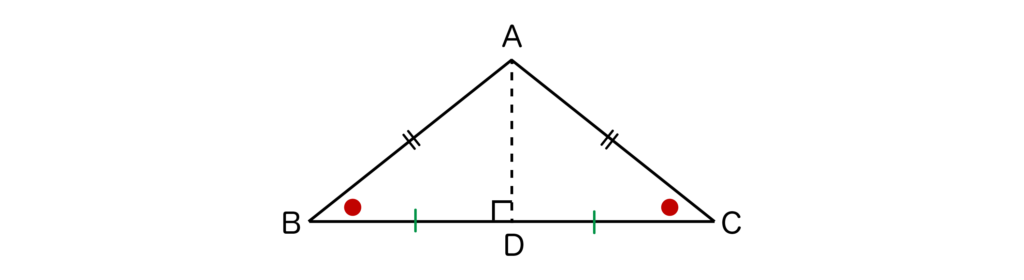
ちなみにですが、先ほど以下の図のような∠=30°の二等辺三角形の頂角の大きさを求めましたね。

∠A=120°より∠BAD=60°となり、∠BDA=90°であることから三角形ABDは60°型の直角三角形となります。
つまり、AD:AB:BD=1:2:√3となります。
以上のことを活用して、頂角が120°である二等辺三角形は1辺の長さがわかっていれば面積も求めることが可能です。
詳しくは二等辺三角形の面積の求め方について解説した記事をご覧ください。
いかがでしたか?
今回は二等辺三角形辺の角度の求め方について解説しました。
二等辺三角形辺の角度の求め方は非常に簡単であることがご理解いただけたかと思います。特に最後で解説した、頂角から底辺に対して垂線をおろすというテクニックは非常に重要です。必ず性質を理解しておきましょう。