三角関数の分野では2直線のなす角を求める問題が出題されます。
2直線のなす角を求める方法はいくつかあるのですが、三角比のtanを活用するのが最も簡単です。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が2直線のなす角の求め方をわかりやすく解説していきます。
tanθ=傾きになる理由から丁寧に解説していくので、数学が苦手な人もぜひ最後までご覧ください。
2直線のなす角を求める前に、tanと傾きの関係を理解しよう
まずはtanと傾きの関係を理解しましょう。
単位円を書き、原点Oを通る傾きがmの一次関数y=mxと単位円との交点を以下のように点P(p、q)とします。そして、点Pからx軸に対して下ろした垂線とx軸との交点をQとし、y=mxとx軸がなす角をθとします。
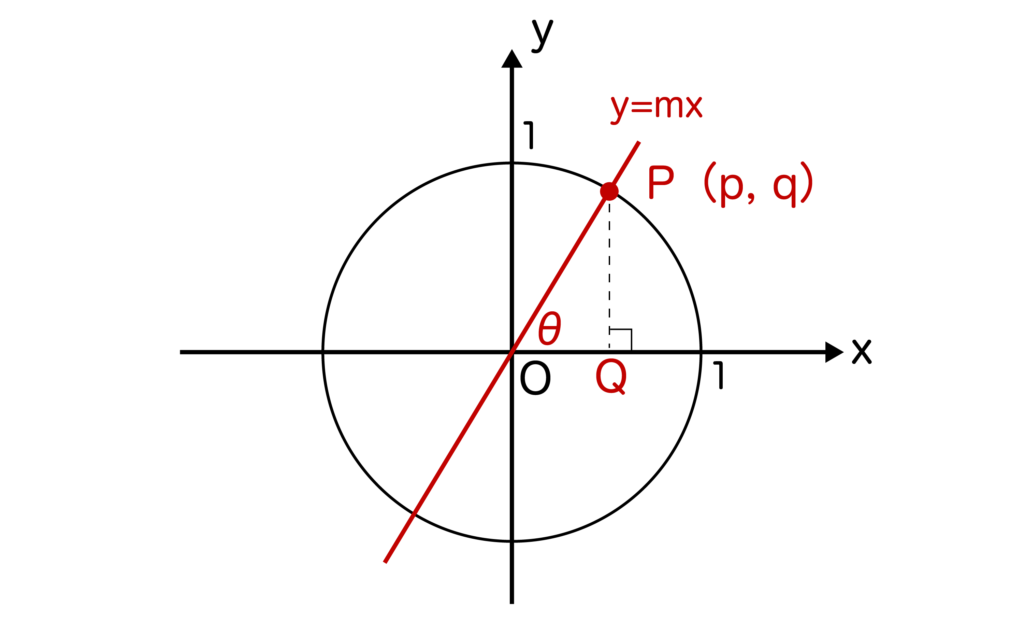
すると、tanθ=q/pとなりますね。
※tanθの求め方がわからない人は三角比の覚え方について解説した記事をご覧ください。
ここで、原点Oと点Pに注目したとき、変化の割合=q/pとなりますね。点Pは一次関数y=mx上にあるので、変化の割合=傾きmとなります。
※変化の割合、傾きがわからない人は一次関数の変化の割合・傾きの求め方について解説した記事をご覧ください。
つまり、変化の割合q/p=傾きmが成り立ちます。ここで、変化の割合q/pは上記の通りtanθでもあるので、tanθ=mが成り立つことがわかります(0°≦θ<90°、90°<θ<180°)
tanθ=mは非常に重要なので、三角関数の公式の1つとして必ず覚えておきましょう。
2直線のなす角の求め方
では、以上のtanθ=mを活用して2直線のなす角の求め方を例題で解説していきます。
【例題1】
2つの直線y=-1/√3xとy=1/√3xがx軸の正の向きとなす角をそれぞれα、βとする。このときα、βを求めなさい。また、2つの直線がなす鋭角も求めなさい。ただし、0°<α<180°、0°<β<180°とする。
【解答&解説】
まずは問題文に書かれていることを以下のように図にしてみましょう。
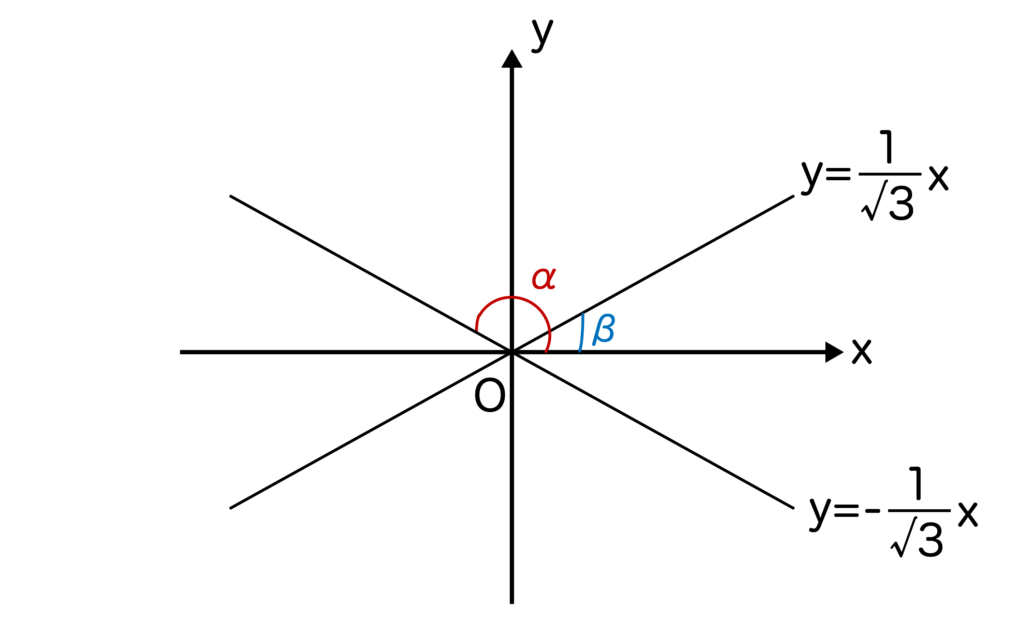
したがって、tanα=-1/√3より、α=150°が求まります。
また、tanβ=1/√3より、β=30°が求まります。
したがって、2つの直線のなす角はα-β=150°-30°=120°>90°なので、求める鋭角=180°-120°=60°となります。
では、もう1つ例題を解いてみましょう。
【例題2】
2直線y=-√3xとy=x+1のなす鋭角を求めなさい。
【解答&解説】
こちらもまずは問題文を図にしてみます。y=-√3x、y=x+1のy>0の部分とx軸の正の向きとのなす角をそれぞれα、βとします。
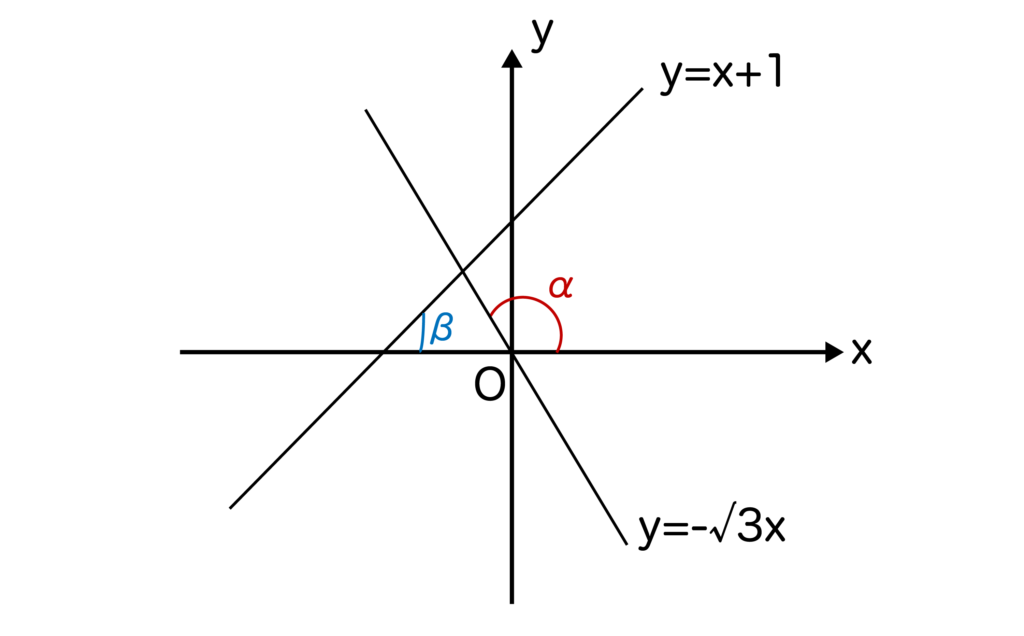
すると、0°<α<180°、0°<β<180°より、
tanα=-√3、tanβ=1が成り立つのでα=120°、β=45°が求まります。
図より、求める鋭角=α-β=120°-45°=75°となります。
2直線のなす角(練習問題)
最後に、2直線のなす角の求め方の練習問題を解きましょう。
tanθ=mをしっかり活用していきましょう。
【練習問題】
2直線y=√3xとy=1/√3xがなす鋭角θを求めなさい。
【解答&解説】
今回もまずは問題文をもとに図を書きましょう。2直線がなすx軸の正の向きとのなす角をそれぞれα、βとします。
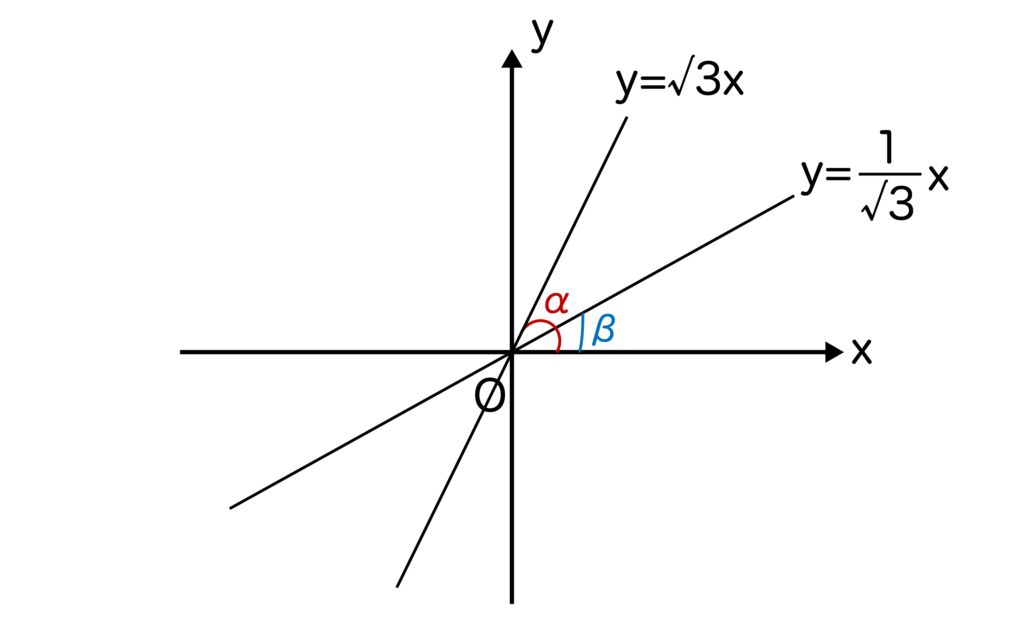
すると、0°<α<180°、0°<β<180°で
tanα=√3、tanβ=1/√3より、
α=60°、β=30°となりますね。
したがって、θ=α-β=60°-30°=30°となります。
いかがでしたか?今回は2直線のなす角の求め方について解説したいきました。
特にtanθ=mは大学入試や共通テストでも頻出です。公式として必ず覚えておきましょう。