二次方程式の学習では実数解という用語が登場しますが、実数解の意味はしっかりと把握できていますでしょうか?
実数解とは何かを把握するには実数が何かを理解してなければなりません。
そこで本記事では早稲田大学教育学部数学科を卒業した筆者が、二次方程式の実数解とは何かについて解説した後、二次方程式が実数解を持つ条件について解説します。
数学が苦手な人でも理解できるよう、わかりやすく解説しているのでぜひ最後までご覧ください。
※二次方程式とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。
二次方程式の実数解とは?
まずは実数解とは何かについて解説します。
実数解とは、その文字の通り実数である解のことです。
実数は有理数と無理数の総称です。そして、有理数は整数・有限小数・循環小数に分けることができます。
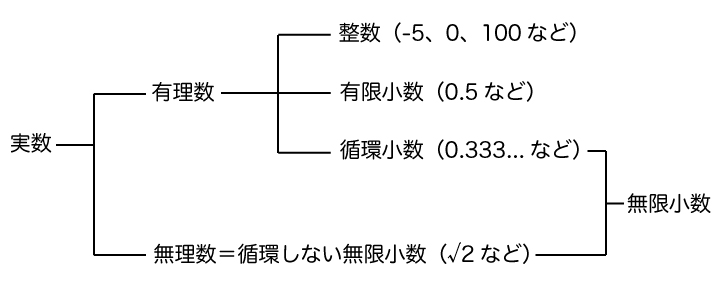
※詳しくは実数とは何かについて解説した記事をご覧ください。
つまり、二次方程式が実数解を持つということは、二次方程式を解くとxの値が実数になるということです。
ちなみにですが、0も実数なのである二次方程式を解いた結果、x=0という解が登場してもそれは実数解となります。
ちなみに、実数解の反対は虚数解です。虚数は「i」を使って表すことができ、i2=-1となるのですが、詳細は数学2で学習するため本記事では割愛させていただきます。
二次方程式が実数解を持つ条件
二次方程式の判別式について詳しく解説した記事をご覧いただくとわかりますが、二次方程式y=ax2+bx+cがあったとき、判別式D=b2-4acについて以下3つが成り立つのでした。
- D>0 ⇔ 異なる2つの実数解を持つ
- D=0 ⇔ ただ1つの実数解を持つ(重解)
- D<0 ⇔ 実数解を持たない
よって、二次方程式ax2+bx+cが実数解を持つための条件は上記1と2を合わせて、D=b2-4ac≧0となります。「≧」なので、D=0でも問題ありません。
※記号「≧」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。
ちなみに、二次方程式ax2+bx+cにおいてbが偶数のとき、判別式D/4=b’2-ac(b=2b’とする)となるのでした。
その場合でも実数解を持つための条件は先ほどと変わりません。つまり、D/4=b’2-ac≧0となります。
二次方程式が実数解を持つことをグラフで表現
上記で解説した通り、二次方程式が実数解を持つということは
- D>0 ⇔ 異なる2つの実数解を持つ
- D=0 ⇔ ただ1つの実数解を持つ(重解)
のどちらかが成り立つということでした。
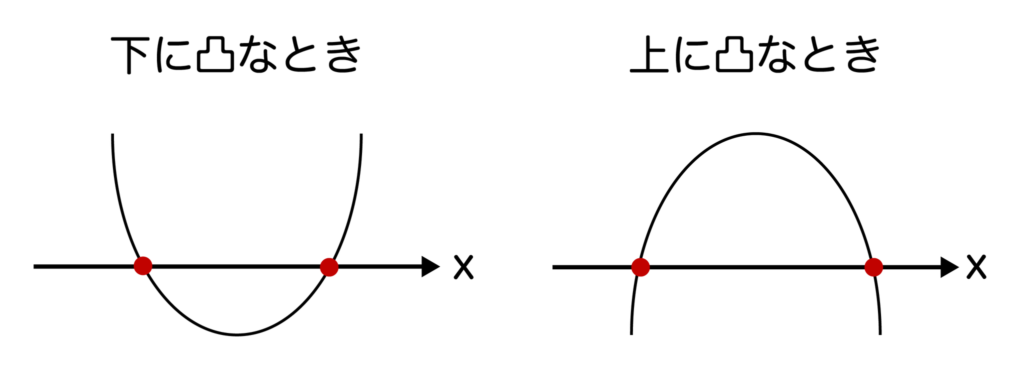
1をグラフで表現すると以下のようになるのでしたね。x座標の数字はすべて実数なので、確かに異なる2つの実数解を持っていることがわかります。
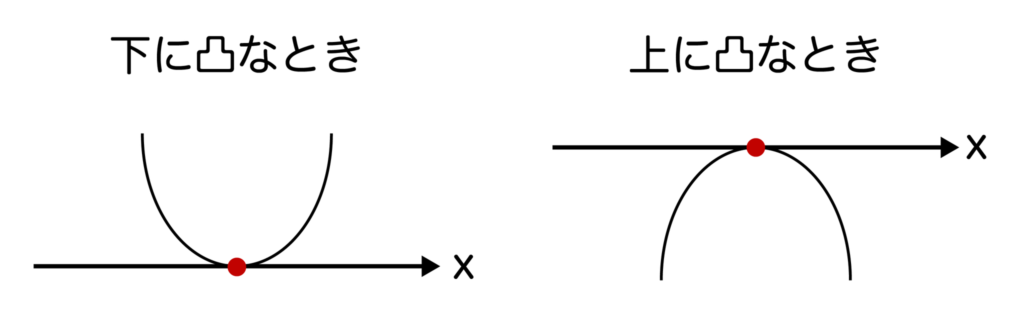
また、2はグラフで表現すると以下のようにx軸と1点で接するのでした。上記と同様にx座標の数字はすべて実数なので、確かにただ1つの実数解を持っていることがわかります。
二次方程式の実数解に関する練習問題
ここからは、二次方程式の実数解に関する練習問題を解いていきましょう。
判別式D=b2-4ac≧0を意識して問題を解いてみてください。
【練習問題】
(1)二次方程式x2+3x+a=0が実数解を持つように、定数aの値の範囲を定めよ。
(2)xに関する二次方程式x2-2ax+a2+a-5=0が実数解を持つとき、aの値の範囲を求めよ。
(3)2つの二次方程式x2+2mx+m+2=0とx2+mx+m=0がともに実数解を持つように定数mの値の範囲を定めよ。
【解答&解説】
(1)二次方程式が実数解を持つための条件は判別式D≧0なので、
32-4×1×a≧より、a≦9/4・・・(答)となります。
(2)xの係数が-2aで偶数となっているので、D/4の判別式を使いましょう。
二次方程式が実数解を持つための条件は判別式D/4≧0なので、
a2-1×(a2+a-5)≧0より、-a+5≧0となるので、a≦5・・・(答)となります。
(3)x2+2mx+m+2=0の判別式D1=m2-m-2=(m+1)(m-2)
x2+mx+m=0の判別式D2=m2-4m=m(m-4)ですね。
ともに実数解を持つのはD1≧0かつ、D2≧0のときですね。
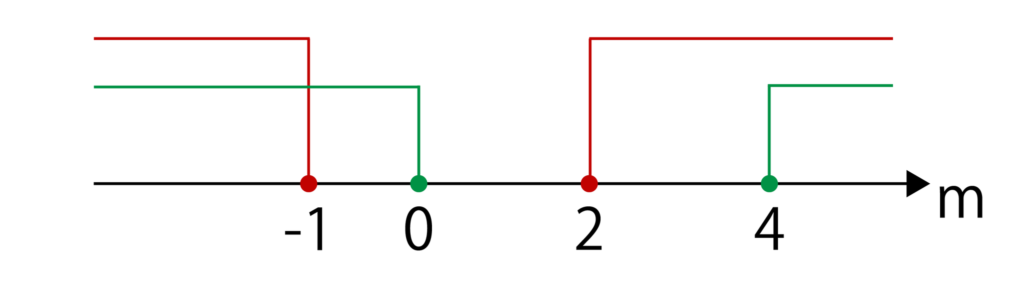
つまり、(m+1)(m-2)≧0かつ、m(m-4)≧0なので、
m≦-1、m≦2かつ、m≦0、4≦mより、以下の図からm≦-1、4≦m・・・(答)となります。
※図の意味が理解できない人は一次不等式とは何かについて解説した記事をご覧ください。
今回は二次方程式の実数解とは何か、二次方程式が実数解を持つ条件について解説していきました。
二次方程式が実数解を持つには判別式D≧0になればよいということを必ず覚えておきましょう。


