大学入試や共通テストでは、二次関数のグラフをx軸やy軸、原点に関して対称移動するという手法を使うケースがあります。
二次関数の対称移動は重要な手法なので必ずやり方を覚えておかなくてはなりません。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が二次関数の対称移動3パターンについて図解でわかりやすく解説していきます。
最後には二次関数の対称移動に関する練習問題も用意しているので、ぜひ最後までご覧ください。
二次関数の対称移動とは?
対称移動とは平面上で図形上の各点を直線や点に関してそれと対称な位置に移すことです。
なので、例えばある二次関数をx軸に関して対称移動させると以下のようになります。
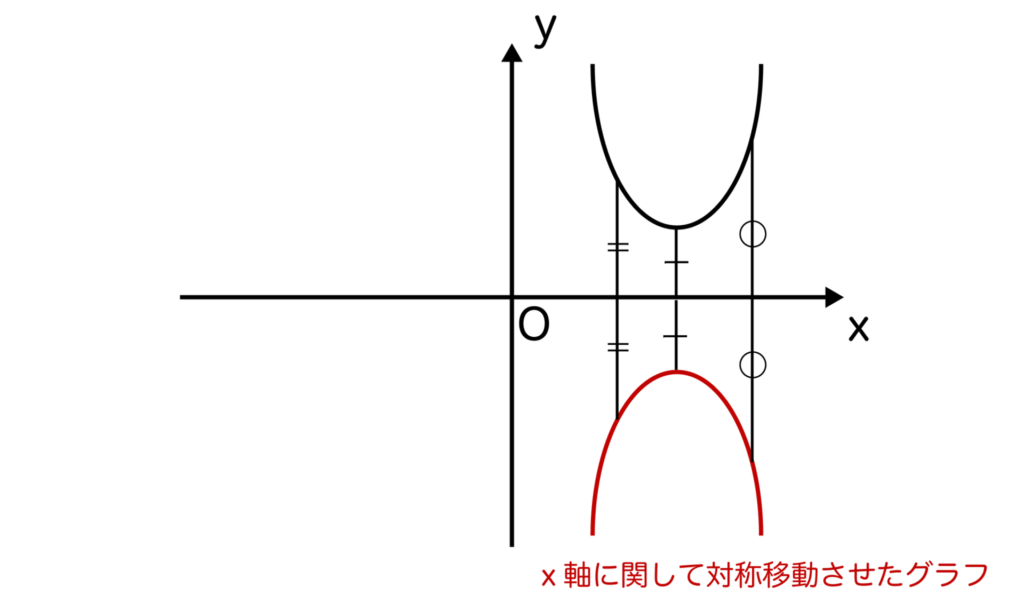
二次関数の対称移動では、
- x軸に関して対称移動させる
- y軸に関して対称移動させる
- 原点に関して対称移動させる
の3パターンがあります。それぞれ順番に解説して行きます。
x軸に関して二次関数を対称移動させる
例えば、点(5、3)をx軸に関して対称移動させると(5、-3)になりますね。
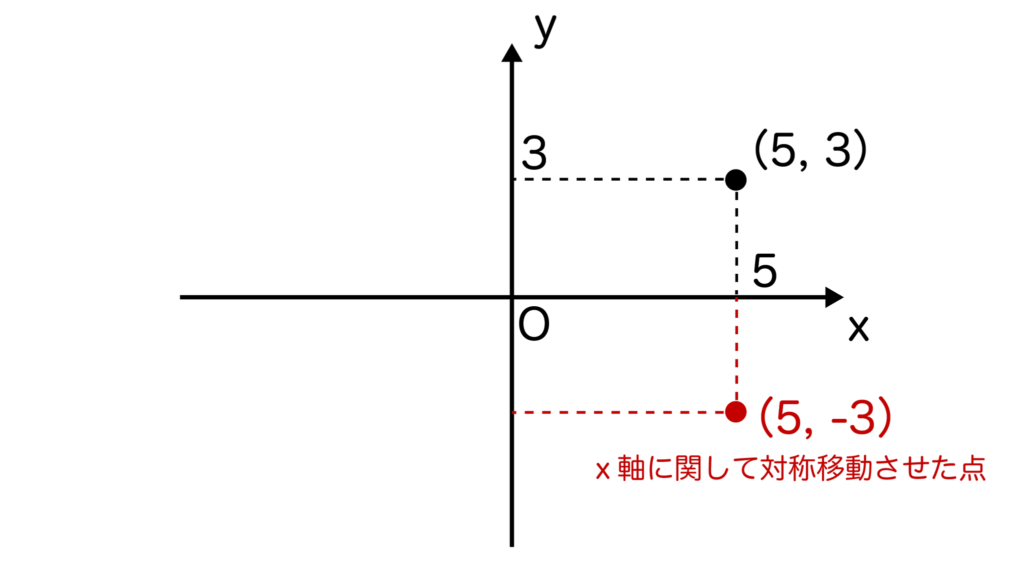
つまり、点(a、b)をx軸に関して対称移動させると点(a、-b)になります。aは変わらずで、bが-bになるのです。
二次関数y=ax2+bx+cについても同様です。二次関数y=ax2+bx+cをx軸に関して対称移動させると、xはそのままでyが-yになります。
つまり、-y=ax2+bx+cより、y=-ax2-bx-cとなるのです。
例題を1つ見てみましょう。
【例題】
二次関数y=2x2+5x-4をx軸に関して対称移動させた二次関数の式を求めよ。
【解答&解説】
上記で解説した通り、x軸に関して対称移動させる場合はxはそのままでyを-yに置き換えます。
つまり、-y=2x2+5x+4となるので、y=-2x2-5x+4・・・(答)となります。
y軸に関して二次関数を対称移動させる
続いては、y軸に関して二次関数を対称移動させるパターンです。
例えば、点(5、3)をy軸に関して対称移動させると(-5、3)になりますね。
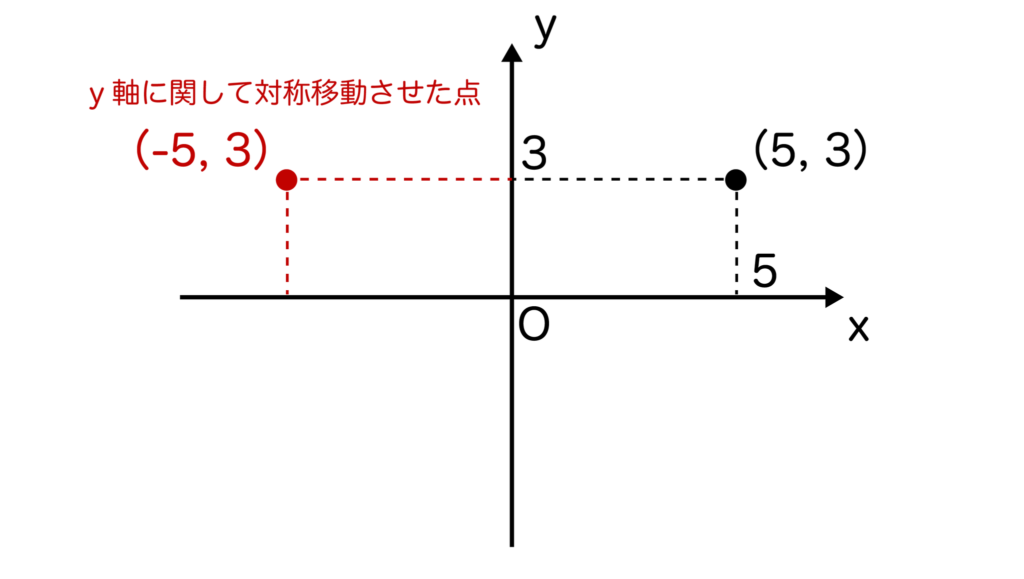
点(a、b)をy軸に関して対称移動させると点(-a、b)になります。bは変わらずで、aが-aになります。
x軸に関して対称移動させるときと逆になります。
なので、二次関数y=ax2+bx+cをy軸に関して対称移動させると、yはそのままでxが-xになります。
つまり、y=a(-x)2+b(-x)+c=ax2-bx+cとなります。
こちらも例題で考えてみましょう。
【例題】
二次関数y=3x2+2x-6をy軸に関して対称移動させた二次関数の式を求めよ。
【解答&解説】
上記で解説した通り、y軸に関して対称移動させる場合はyはそのままでxが-xに置き換わります。
つまり、y=3(-x)2+2(-x)-6=y=3x2-2x-6・・・(答)となります。
原点に関して二次関数を対称移動させる
最後は原点に関して二次関数を対称移動させるパターンです。
点(5、3)を原点に関して対称移動させると点(-5、-3)になります。
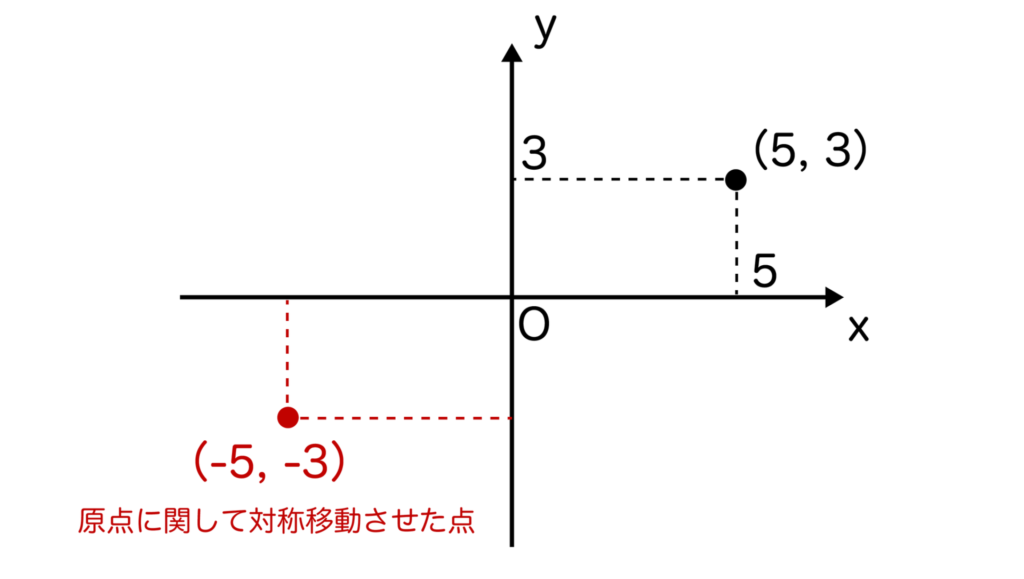
点(a、b)を原点に関して対称移動させると点(-a、-b)になります。aもbも符号が変わりますのでご注意ください。
よって、二次関数y=ax2+bx+cを原点に関して対称移動させると、xが-xになり、yが-yになります。
つまり、-y=a(-x)2+b(-x)+c=ax2-bx+cとなるので、y=-ax2+bx-cとなります。
では、例題です。
【例題】
二次関数y=4x2-5x+10を原点に関して対称移動させた二次関数の式を求めよ。
【解答&解説】
xが-xに、yが-yに置き換わるので、
-y=4(-x)2-5(-x)+10=4x2+5x+10より、y=-4x2-5x-10・・・(答)となります。
以上が二次関数の対称移動に関する解説となります。そこまで難しい内容ではなかったと思います。
まとめると、
- x軸に関して対称移動=yが-yに
- y軸に関して対称移動=xが-xに
- 原点に関して対称移動=xが-xに、yが-yに
となります。必ず覚えておきましょう。
二次関数の対称移動と平行移動
共通テストでは、たまに対称移動と平行移動を組み合わせた問題が出題されるときがありますので、対策が必須です。1つ例題をご紹介します。
※平行移動がわからない人は二次関数の平行移動について解説した記事をご覧ください。
【例題】
二次関数y=x2+ax+bを原点に関して対称移動させ、その後x軸方向に-1、y軸方向に8だけ平行移動させるとy=-x2+5x+11になった。
このとき、aとbの値を求めよ。
【解答&解説】
二次関数y=x2+ax+bを原点に関して対称移動させると、
-y=(-x)2+a(-x)+b=x2-ax+bより、y=-x2+ax-bとなりますね。
これをx軸方向に-1、y軸方向に8だけ平行移動させると、
y=-(x+1)2+a(x+1)-b+8=-x2+(a-2)x+a-b+7となりますね。
問題文より、-x2+(a-2)x+a-b+7=-x2+5x+11が成り立つので、a=7、b=3・・・(答)が求まります。
※xの係数に注目すると(a-2)=5となるのでa=7となります。あとはa-b+7と11を見比べれば良いです。係数が何かわからない人は多項式の定義について解説した記事をご覧ください。
二次関数の対称移動に関する練習問題
ここからは二次関数の対称移動に関する練習問題となります。上記で学習したことをしっかり理解していれば難しくありません。
【練習問題1】
二次関数y=5x2+3xを(1)x軸、(2)y軸、(3)原点のそれぞれに関して対称移動させたときの二次関数の式を求めよ。
【解答&解説】
(1)x軸に関して対称移動させるので、yを-yに置き換えます。
-y=5x2+3xより、y=-5x2-3x・・・(答)となります。
(2)y軸に関して対称移動させるので、xを-xに置き換えます。
y=5(-x)2+3(-x)=5x2-3x・・・(答)となります。
(3)原点に関して対称移動させるので、xを-xに、yを-yに置き換えます。
-y=5(-x)2+3(-x)=5x2-3xより、y=-5x2+3x・・・(答)となります。
【練習問題2】
二次関数y=x2をx軸方向にp、y軸方向にqだけ平行移動させた後、x軸に関して対称移動したところ二次関数の式はy=-x2-6x+8となった。
このとき、pとqの値を求めよ。
【解答&解説】
y=x2をx軸方向にp、y軸方向にqだけ平行移動させると、y=(x-p)2+qとなりますね。
これをx軸に関して対称移動させるので、yを-yに置き換えて、
-y=(x-p)2+qより、y=-(x-p)2-qとなります。
y=-(x-p)2-qを展開するとy=-x2+2px-p2-qより、y=-x2-6x+8と見比べると
- 2p=-6
- -p2-q=8
となるので、p=-3、q=-17・・・(答)となります。
※展開のやり方がわからない人は多項式の計算について解説した記事をご覧ください。
ちなみにですが、y=-(x-p)2-qを求めた後、それを展開するのではなくy=-x2-6x+8を平方完成して見比べても問題ありません。
y=-x2-6x+8を平方完成するとy=-(x+3)2+17となるので、y=-(x-p)2-qと見比べてp=-3、q=-17を求めることもできます。
※平方完成のやり方がわからない人は二次関数の平方完成の公式・やり方について解説した記事をご覧ください。
いかがでしたでしょうか?
今回は二次関数の対称移動のやり方について解説しました。そこまで難しい内容ではないと思いますので、ぜひこれを機にしっかりと内容を理解しておきましょう。


