高校数学の数学1では二次関数が登場しますが、その前に中学数学の復習として一次関数を取り上げている教科書や参考書も多いです。
なので、本サイトでも一次関数を念のため取り上げておきます。
本記事では、早稲田大学教育学部数学科を卒業した筆者が一次関数とは何か、直線の式の求め方やグラフの書き方だけでなく切片などの重要用語も合わせて解説します。
数学が苦手な人でも理解できるようわかりやすく解説しているので、ぜひ最後までお読みください。
一次関数とは?直線の式は?
一次関数とは何かについて解説する前に、まずは関数とは何かについて簡単に解説しておきます。
2つの変数xとyがあり、xの値を定めるとyの値がただ1つだけ定まるとき、yはxの関数であるといいます。
※変数とは何かについて詳しく解説した記事もぜひ合わせてご覧ください。
一次関数はy=ax+bと表すことができ、xの一次式であることから一次関数と言われています(a、bは定数。a≠0とする)
※一次式がわからない人は、多項式の定義や次数について解説した記事をご覧ください。
一次関数の例としてy=2x+8を考えてみましょう。
x=4のとき、y=2×4+8=16となり、yの値がただ1つだけ決まることが確認できます。
y=ax+bは一次関数を表す直線の式として基本中の基本なので、必ず頭に入れておきましょう。
一次関数の傾き・切片について
一次関数y=ax+bにおいて、aのことを傾き、bのことを切片と呼びます。
a>0のとき、グラフは右上がりのグラフとなります。
※記号「>」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。
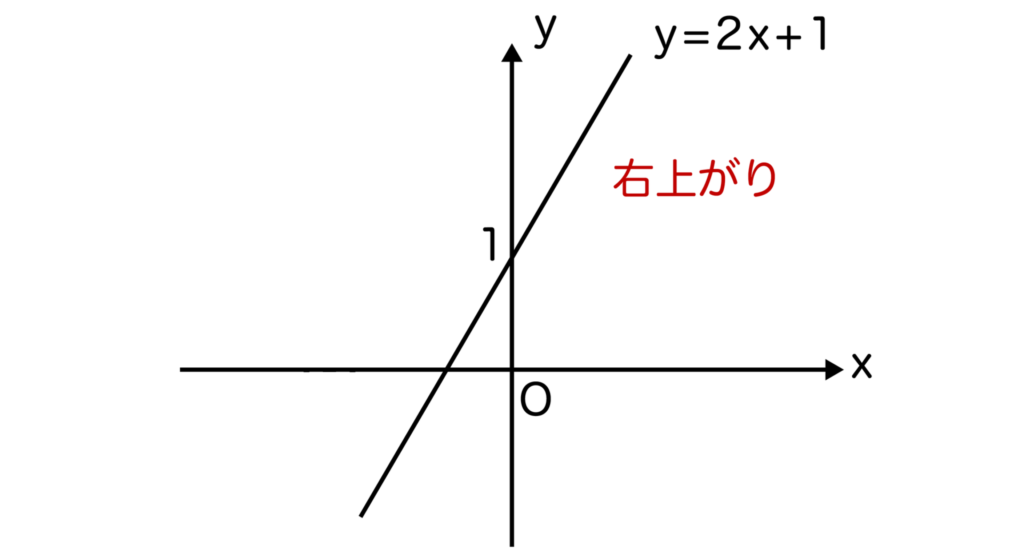
例えば、y=2x+1を考えてみましょう。
x=1のときy=3、x=2のときy=5、x=3のときy=7・・・とxの値が増加するにつれてyの値も増加しますね。
よって、グラフは右上がりのグラフとなります。また、切片はx=0のときのyの値のことを指しています。
x=0のときy=1なので、y=2x+1の切片は1となります。
※一次関数のグラフの書き方は後ほど解説します。
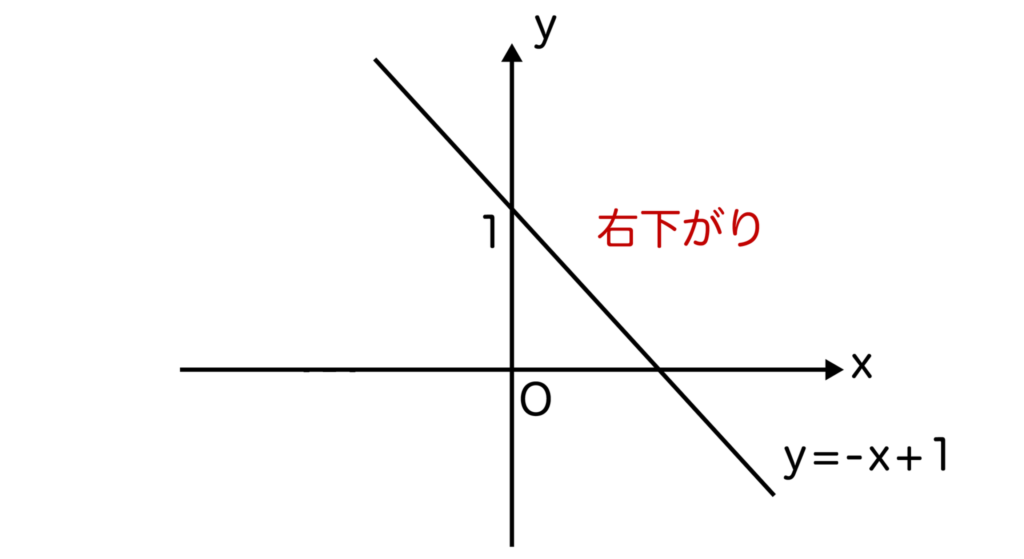
a<0のとき、グラフは右下がりのグラフとなります。
今度はy=-x+1を考えてみましょう。
x=1のときy=0、x=2のときy=-1、x=3のときy=-1・・・と今度はxの値が増加するにつれてyの値は減少しますね。
よって、グラフは右下がりのグラフとなります。また、x=0のときy=1なので、切片は1です。
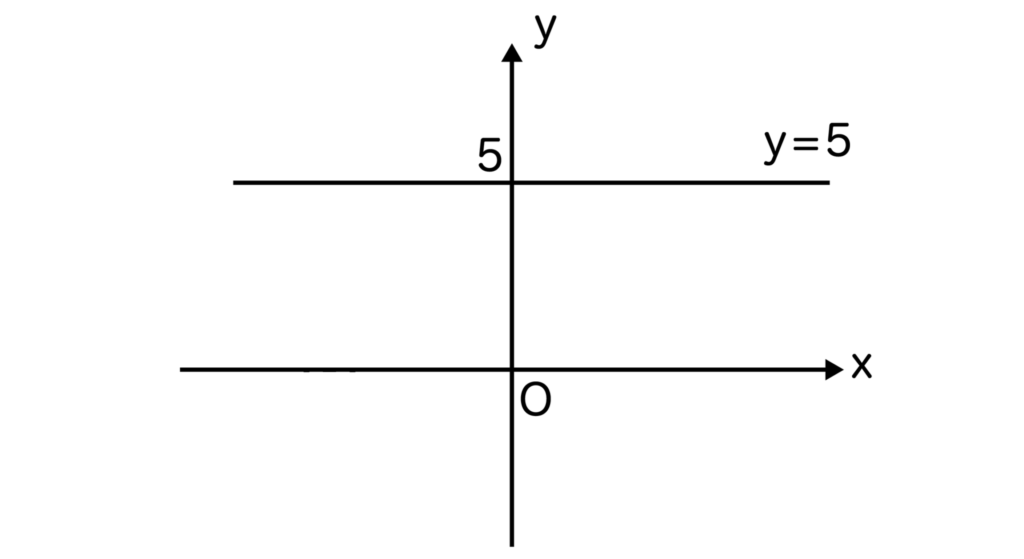
ちなみに、先ほどから一次関数y=ax+bにおいてはa≠0であることを記載していますが、a=0のときはy=bとなり、xに関する一次式にはならないので一次関数とは呼びません。
例えば、y=5のグラフはxがどんな値を取ろうともy=5になるグラフなので、以下のようになります。
一次関数の求め方・グラフの書き方
一次関数のグラフの書き方は簡単なのでご安心ください。
以下4つのパターンにそって解説していきます。
パターン1:グラフの式がわかっている場合
一次関数は必ず直線のグラフとなるので、その直線が通る2点がわかればグラフは書けます。
では、例としてy=x+2のグラフを書いてみましょう。
すでに一次関数の直線の式がわかっている場合は自分で勝手に2点を決めてしまいましょう。
例えば、x=0のときy=2、x=1のときy=3なので、点(0,2)と点(1,3)を通る直線を書けば問題ありません。
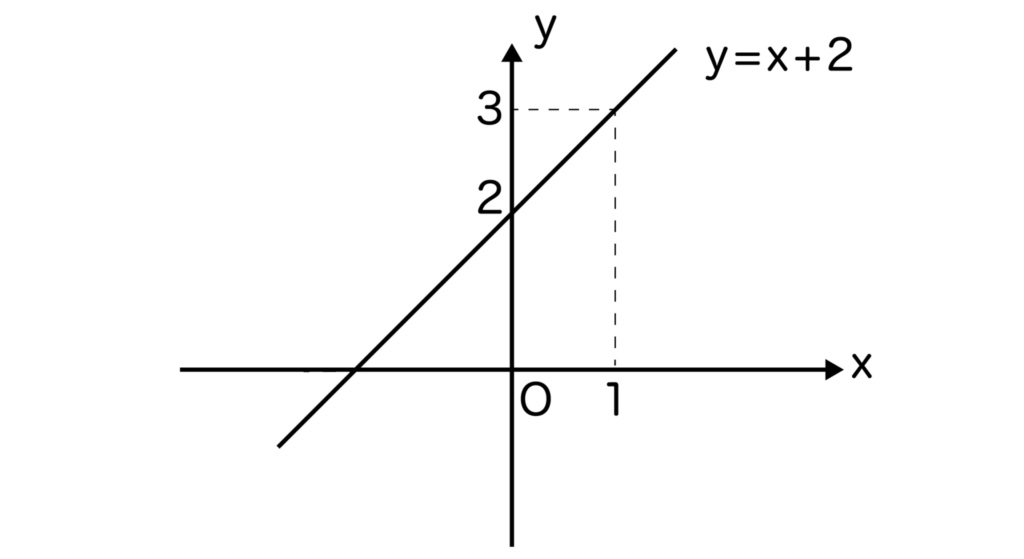
パターン2:傾きがわかっている場合
傾きだけがわかっていて、切片がわからないパターンです。例題をみてみましょう。
【例題】
傾きが2で点(3,7)を通る一次関数の直線の式を求めて、グラフを書きなさい。
【解答&解説】
傾きが2であるということは求める一次関数はy=2x+bと表すことができますね。
この一次関数が(3,7)を通るので、y=2x+bに(3,7)を代入して、
7=2×3+bとなり、b=1が求まります。
よって、求める一次関数の直線の式はy=2x+1となります。
y=2x+1はx=0のときy=1なので、(0,1)と(3,7)を結んでグラフは書けます。
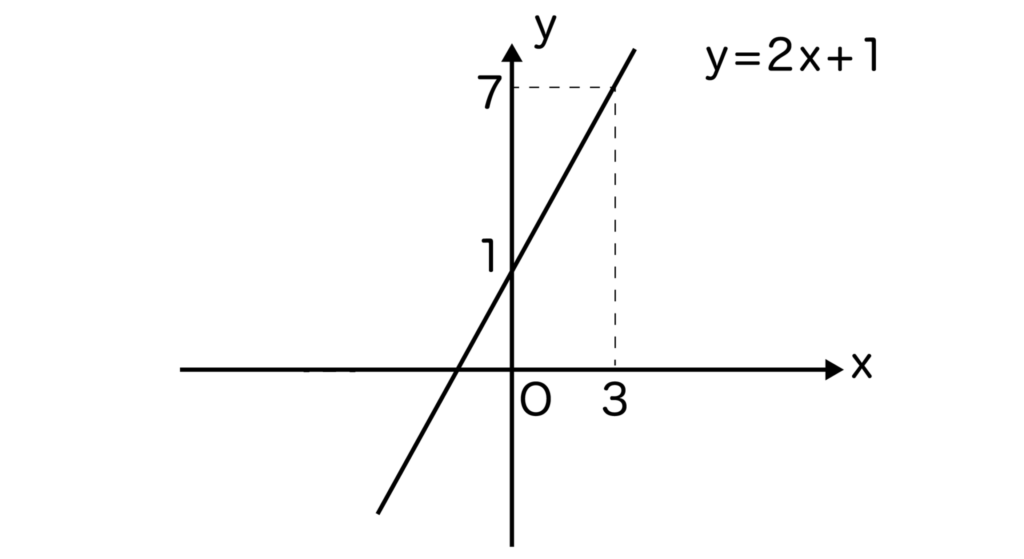
パターン3:切片がわかっている場合
今度は切片がわかっていて傾きがわかっていないパターンです。例題をみてみましょう。
【例題】
切片が1で点(2,7)を通る一次関数の直線の式を求めて、グラフを書きなさい。
【解答&解説】
切片が1ということは求める一次関数はy=ax+1と表すことができます。
この一次関数が(2,7)を通るので、7=2a+1より、a=3となります。
よって求める一次関数はy=3x+1となります。
x=0のときy=1なので、(0,1)と(2,7)を結んでグラフを書きましょう。
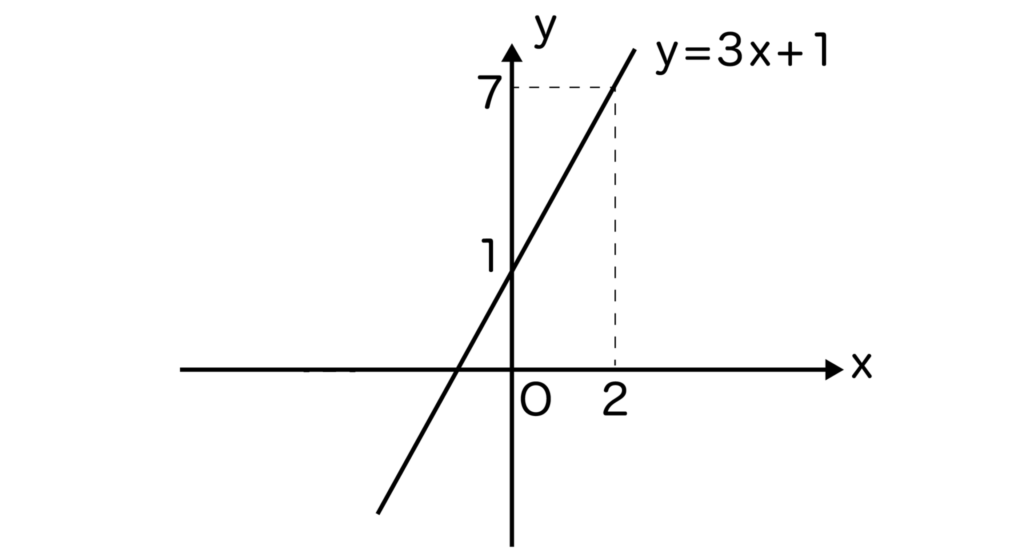
パターン4:傾きも切片もわからない場合
最後は傾きも切片もわからない状態から一次関数の直線の式を求めるパターンです。
傾きも切片もわからないときは、その一次関数が通る点が必ず2点用意されます。
【例題】
(-4,7)と(1,-3)を通る一次関数の直線の式を求めて、グラフを書きなさい。
【解答&解説】
一次関数はy=ax+bで表すことができるので、(-4,7)と(1,-3)をy=ax+bに代入すると、
- 7=-4a+b・・・①
- -3=a+b・・・②
となります。①-②より、10=-5aとなるので、a=-2となります。
a=-2を②に代入して、b=-1が求まります。
よって求める一次関数の直線の式はy=-2x-1となります。
問題文より(-4,7)と(1,-3)を通るので、グラフは以下となります。
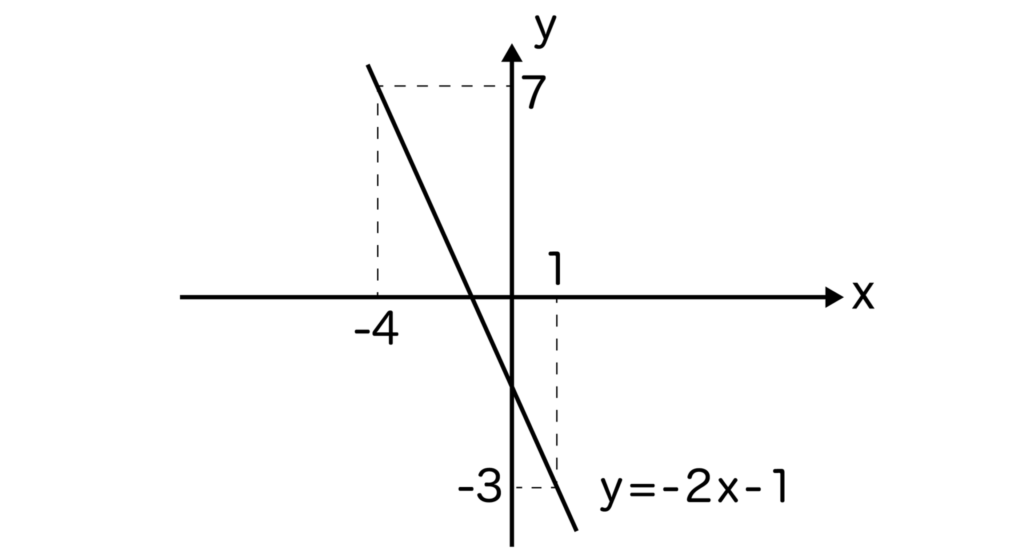
一次関数の直線の式に分数がある場合のグラフ
一次関数の直線の式に分数があるグラフを書くには少し工夫が必要です。
こちらも例題で解説していきます。
【例題】
一次関数y=1/5x+2のグラフを書け。
【解答&解説】
上記でも解説しいる通り、一次関数y=1/5x+2が通る2点を決める必要があります。
今回の場合、xの係数が1/5なのでx=-5や5、10、15のときのyの値を考えると計算がしやすくなります。
x=-5のときy=1、x=5のときy=3なので、グラフは以下のようになります。
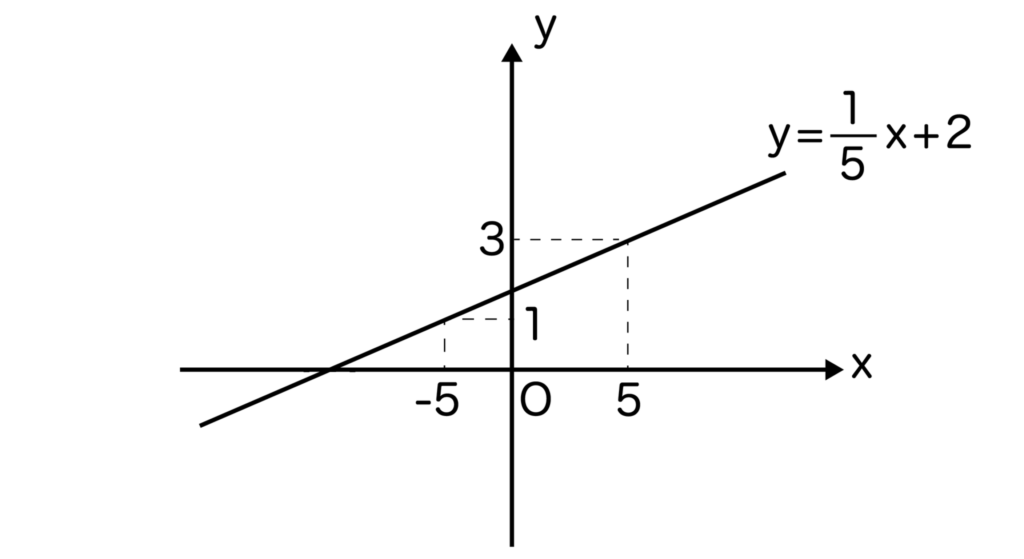
このように、一次関数の直線の式に分数がある場合はなるべく計算がしやすくなるxの値を考えると良いです。
一次関数と象限
一次関数に限った話ではないですが、x軸・y軸で分けられた座標平面の4つの部分をそれぞれ以下のように第1象限、第2象限、第3象限、第4象限と言います。
x座標、y座標の符号でどの象限かを判断します。
第1象限から反時計まわりに第2象限、第3象限、第4象限となると覚えておきましょう。
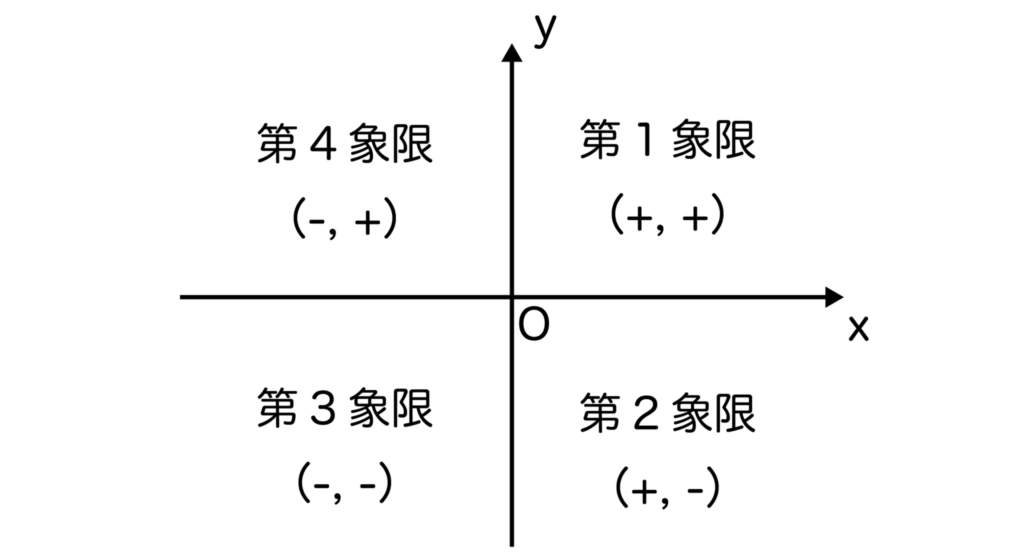
例えば、xが+でyも+ならば、その点は第1象限に属します。
xが-でyが+ならば、その点は第2象限に属します。
ちなみに、x軸・y軸上の点はどの象限にも属さないとするのでご注意ください。
一次関数の交点の求め方
2つの一次関数があるとき、その一次関数の交点は連立方程式を解くことで求めることができます。
例題で解説していきます。
【例題】
一次関数y=3x+5とy=-x+2の交点を求めよ。
【解答&解説】
交点は連立方程式
- y=3x+5
- y=-x+1
を解くことで求めることができます。
つまり、3x+5=-x+1より、4x=-4となるのでx=-1となります。
x=-1より、y=2となるので交点は(-1,2)となります。
交点の求め方は全然難しくないと思います。一次関数の超基本事項なので必ずできるようにしておきましょう。
一次関数の定義域と値域
関数では変域という概念が登場します。
x・yが変化できる値(=領域)が決まっているとき、それを「xの変域」「yの変域」と言います。
例えば、y=2x+5という一次関数があったとき、xの変域が2≦x≦5ならyの変域は9≦y≦15となります。
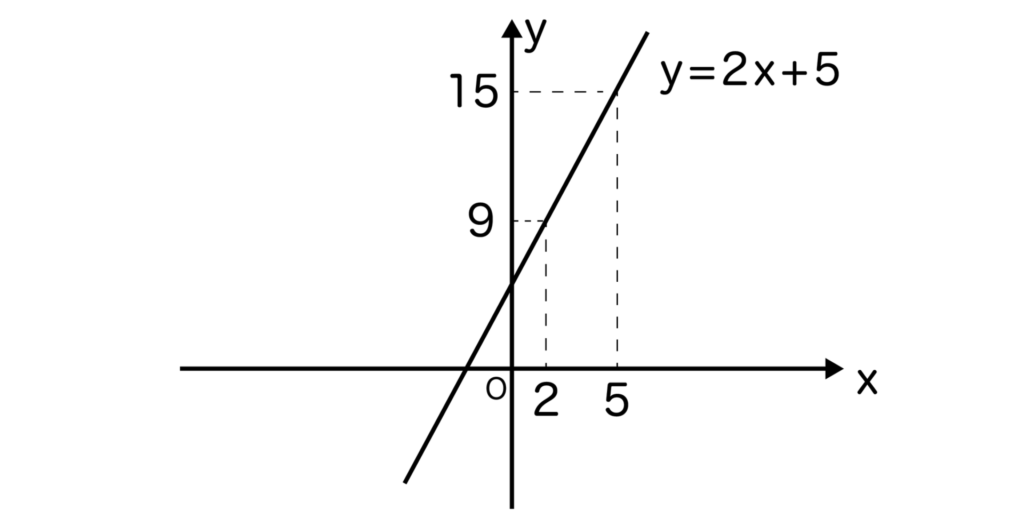
xの変域は定義域、yの変域は値域と呼ばれており、定義域・値域は大学入試や共通テストでも頻出なので、必ず覚えましょう。
詳しくは一次関数の変域について解説した記事をご覧ください。
一次関数の変化の割合
一次関数では変化の割合という超重要用語が登場するので、かならず覚えておきましょう。
変化の割合とはxが1増加したときに、yがどれだけ増加(または減少)するかを示したものです。
一次関数では変化の割合=傾きとなります。
例えば、y=-5x+9の傾きは-5なので、変化の割合も-5となります。
実際に検算してみます。
x=0のときy=9、x=1のときy=4ですね。xが1増加するとyは4増加しているので、確かに変化の割合=4になっていることがわかります。
変化の割合(傾き)はyの増加量/xの増加量でも求めることができます。
※詳しくは一次関数の変化の割合について解説した記事をご覧ください。
これを利用すると、2点を通る一次関数の直線の式が少しだけ求めやすくなります。
例えば、上記で(-4,7)と(1,-3)を通る一次関数の直線の式を求める例題をご紹介し、連立方程式を使って一次関数の直線の式を求めましたが、これを変化の割合(傾き)=yの増加量/xの増加量を使って解いてみます。
xが-4から1に変化しているので、xの増加量=1-(-4)=5です。
yが7から-3に変化しているので、xの増加量=-3-7=-10です。
よって、変化の割合(傾き)=-10/5=-2となります。
ここで、求める一次関数の直線の式をy=-2x+bとおいて、(1,-3)を代入すると、
-3=-2+bとなり、b=-1となるので、y=-2x-1が求まります。
連立方程式を使うよりも少しだけ楽に解くことができます。ぜひ1つのテクニックとして覚えておきましょう。
一次関数の練習問題
最後に一次関数の練習問題を解いてみましょう。
すべて基礎問題となっているので、必ず解けるようにしておきましょう。
【練習問題1】
以下の一次関数の直線の式を求めよ。
(1)傾きが6で切片が10の一次関数
(2)傾きが10で点(7,50)を通る一次関数
(3)切片が2で点(5,52)を通る一次関数
(4)点(42,100)と点(8,32)と通る一次関数
【解答&解説】
(1)y=6x+10
(2)傾きが10なので、求める一次関数の直線の式をy=10x+bとおきます。
50=10×7+bより、b=-20となるので、y=10x-20・・・(答)となります。
(3)切片が2なので、求める一次関数の直線の式をy=ax+2とおきます。
52=5a+2より、a=10となるので、y=10x+2・・・(答)となります。
(4)変化の割合(傾き)を利用して解きましょう。
xの増加量=8-42=-34
yの増加量=32-100=-68
より、変化の割合(傾き)=-68 / -34 =2となります。
求める一次関数の直線の式をy=2x+bとおくと、
32=2×8+bより、b=16なので、y=2x+16・・・(答)となります。
【練習問題2】
一次関数y=9x+80とy=-3x-4の交点を求めよ。
【解答&解説】
9x+80=-3x-4より、12x=-84となるので、x=-7が求まります。
x=-7をy=-3x-4に代入して、y=17となるので、交点は(-7,17)・・・(答)となります。
【練習問題3】
以下の点は第何象限の点か答えよ。
(ア)(2,3)
(イ)(-10,-6)
(ウ)(4,-87)
【解答&解説】
(ア)第1象限
(イ)第3象限
(ウ)第2象限
いかがでしたでしょうか?
今回は一次関数の基本的内容と用語について解説していきました。
本記事で解説した内容はすべて基本的なことです。一次関数でつまずくと、この後の二次関数でも絶対につまずいてしまいます。本記事の内容は必ず理解しておきましょう。