高校数学における数学1で最初に登場する分野が多項式です。
多項式自体は中学の数学でも登場していますが、高校数学では多項式のより高度な四則演算(足し算・引き算・掛け算・割り算)を学習します。
しかし、四則演算を行うには多項式に関する用語(項、次数、係数、定数項など)をしっかりと理解しておかなければなりません。
そこで本記事では、早稲田大学教育学部数学科を卒業した筆者が多項式の定義について解説した後、多項式の項とは何か?や次数・係数・定数項など必ず知っておくべき用語についてわかりやすく解説します。
また、多項式と単項式・関数の違いについても解説します。
多項式の定義(単項式との違いも)
多項式の定義を理解する前に、まずは単項式とは何かを理解しましょう。
単項式とは、数と文字を掛け合わせてできている式または数単体のことです。
例えば、10aという式は10×aを意味しています。数(=10)と文字(=a)を掛け合わせてできているので10aは単項式となるわけです。他にも45xや32y、-5pなども単項式となります。
では、30a2はどうでしょうか?30a2=30×a×aを意味しており、数(=30)と文字(=a)の掛け合わせでできているので単項式となります。
50pqrは50×p×q×rを意味しており、これも数(=50)と文字(=p、q、r)の掛け合わせでできるので単項式となります。
数単体とは、文字がない数のことです。例えば、10、965、-52、0.25、2/5などです。整数だけでなく、小数・分数も単項式に含まれます。
一方で、多項式は2個以上の単項式の和として表される式のことです。
例えば、2a+5bは単項式2aと単項式5bの和になっているので多項式と言えます。
5p3+4は単項式5p3と単項式4の和になっているので、これも多項式と言えます。
では、10p-7qはどうでしょうか?和(足し算)ではなく引き算の形になっているので多項式ではないように見えますが、これも多項式となります。
10p-7q=10p+(-7q)と考えることができるためです。+と-が組み合わさると-になるのでしたね。
4a+8aは一見すると多項式のように見えますが、4a+8a=12aとなり計算結果が単項式となるので単項式となります。多項式ではないのでご注意ください。
以上より、
- 掛け算のみで表現できる or 数単体=単項式
- 2個以上の単項式が足し算されている=多項式
と理解すれば問題ないでしょう。
ちなみに、多項式は整式とも呼ばれているので、余力があれば覚えておきましょう。
多項式の項とは?
多項式において、各単項式のことを項と呼びます。
例えば、10a+6b+9cという多項式があったとします。
この時、単項式は10a、6b、9cの3つですね。よって、この多項式の項は10a、6b、9cの3つとなります。
では、9p-3qという多項式の項はどうなるか考えてみましょう。
この場合、単項式は9pと-3qの2つになります。先ほども解説しましたが、9p-3q=9p+(-3q)と考えることができるためです。
したがって、多項式9p-3qの項は9pと-3qになります。
では、多項式5x+5/8の項はどうでしょうか?
先ほども解説した通り、数単体も単項式になるのでした。よって、多項式5x+5/8の単項式(=項)は5xと5/8の2つになります。
多項式の次数とは?
次数は単項式の場合と多項式の場合で考え方が少し異なるので注意が必要です。
単項式における次数とは、掛け合わされている文字の個数のことです。
例えば、30abcという単項式があるとします。この時、掛け合わされている文字はa、b、cの3個なので次数=3となります。
5p3qの場合だと、5p3q=5×p×p×p×qより、掛け合わされている文字は4個なので、次数=4となります。
ちなみに、2や-10、0.25、7/10など数単体の単項式には文字が掛け合わされていないので次数=0となります。
一方で、多項式における次数とは、各項の次数のうちでもっとも大きいもののことです。
例えば、5x2+8y-10zという多項式があるとします。この時、
- 項5x2の次数=2
- 項8yの次数=1
- 項-10zの次数=1
なので、5x2+8y-10zの次数は2となります。
ちなみに、次数がnである多項式をn次式と呼びます。上記の5x2+8y-10zは2次式となります。
多項式の係数とは?
係数とは単項式(項)における数の部分のことを言います。
例えば、7aという単項式の数の部分は7なので、7aの係数は7となります。
単項式-5xの係数は-5となります。
多項式の場合、項の数だけ係数があることになります。
例えば、6x+10y-5zという多項式がある場合、項(単項式)は6x、10y、-5zの3つなので、係数は6、10、-5の3つとなります。
多項式の定数項とは?
多項式において文字を含まない単項式(項)のことを定数項と言います。
例えば15p2+8p+30という多項式があったとき、文字を含まない単項式(項)は30なので、定数項は30となります。
もう1つ例をあげます。多項式0.3x2+5y-9において、文字を含まない単項式(項)は-9なので、定数項は-9となります。
特定の文字に注目した場合の次数・係数・定数項
次数・係数・定数項とは何かを理解したところで、ここからは少し応用的な学習をしましょう。
2種類以上の文字を含む単項式・多項式(例:8ab、6ax2、7ax+10bなど)においては、次数・係数・定数項を考えるときに特定の文字に注目する場合があります。
この時、他の文字(=注目する文字以外の文字)は数と同様に扱います。
例えば、単項式10ax2の次数と係数を考えてみましょう。
何か特別な指示がなければ、次数=3、係数=10で問題ありません。
しかし、稀に「xに注目した場合の次数と係数を答えよ」という指示が出る場合があります。この場合、次数は2で係数は5aとなります。
xに注目するということは、x以外の文字(今回の場合はa)は全て数とみなすということです。
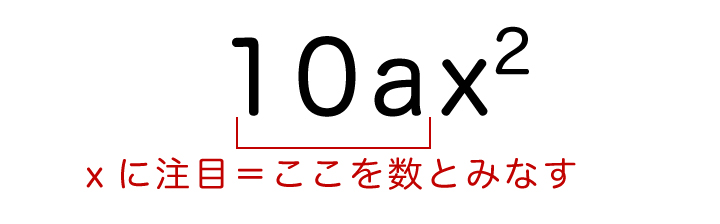
注目する文字は1つとは限りません。例えば、多項式x3-5ax3y+6xy+9y2-5by+4aがあり、xとyに注目したときの次数と定数項を考えてみましょう。
xとyに注目するということは、xとy以外の文字は全て数とみなすということです。
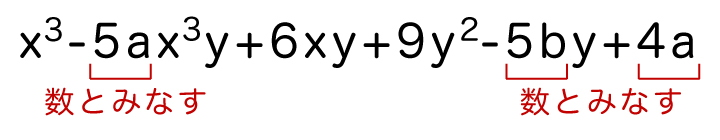
したがって、次数は4(項が-5ax3yの部分)、定数項は4a(xとyを含んでいない項)となります。
※多項式では、次数の高い項から順番に並べるのが一般的とされています。これを降べきの順と言います。
反対に、次数の低い項から順番に並べることを昇べきの順と言います。
詳しくは降べきの順・昇べきの順に整理するやり方について解説した記事をご覧ください。
多項式の同類項とは?
同類項とは多項式において文字の部分が同じである項のことです。
例えば、10a+5b-8a+3bという多項式があったとき、項10aと-8a、5bと3bは文字の部分が同じなので同類項となります。
同類項は1つにまとめることが可能です。
10a-8a=2a、5b+3b=8bとなるので、10a+5b-8a+3b=2a+8bと表現することが可能です。
同類項をまとめるという手法は多項式の計算で必須の知識となっています。
※多項式の計算方法について解説した記事もぜひ合わせてご覧ください。
多項式と関数の違いとは?
以上で単項式・多項式に関する用語はすべて解説しました。用語の意味を理解しておかないと、そもそも問題文の意味が理解できないので、上記でご紹介した用語は必ずマスターしておきましょう。
続いては、多項式と関数の違いについて解説します。
※多項式と関数の違いについては突き詰めるとかなり奥が深く、大学や大学院で学ぶレベルの内容のため、本記事では要点だけ取り上げて解説します。
多項式は上記でも解説した通り、2個以上の単項式(項)から成り立っています。
しかし、関数はそもそも多項式である必要はありません。y=3xも関数の1つです。もちろんy=6x2+3x+10など多項式の形をしている関数もあります。
高校生の時点では多項式は関数の一種だが、関数=多項式ではない(とは限らない)程度に理解しておけば問題ないでしょう。
単項式・多項式の用語を使った練習問題
最後に、上記で取り上げた単項式・多項式に関する用語を使った練習問題をご紹介します。
全て超基本的な問題なので、必ず解けるようにしておきましょう。
【練習問題1】
以下の数や式を単項式と多項式に分けなさい。
50、-100、5b、6a+9b、8y2、10x3+4b
【解答&解説】
単項式=50、-100、5b、8y2
多項式=6a+9b、10x3+4b
【練習問題2】
多項式60x5y+45x2y-30y-70の次数と定数項を答えよ。
【解答&解説】
今回は「特定の文字に注目せよ」という指示はないのでシンプルに考えます。
多項式の次数は各項(単項式)の次数の中でもっとも大きいものでした。
- 項60x5yの次数=6
- 項45x2yの次数=3
- 項-30yの字数=1
- 項-70の次数=0
なので、次数は6・・・(答)となります。
定数項は文字を含まない単項式(項)のこと(=次数が0)でした。なので、定数項は-70・・・(答)となります。
【練習問題3】
多項式a3b2+5ab5c+7c3+9において、aとbに注目したとき、その次数と定数項を答えよ。
【解答&解説】
aとbに注目するので、aとb以外の文字は全て数とみなします。
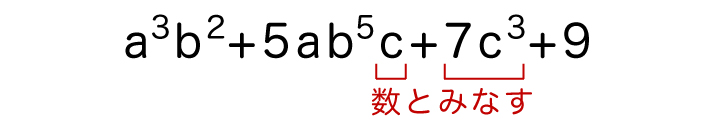
よって、
- 項a3b2の次数=5
- 項5ab5cの次数=6
- 項7c3の次数=0
- 項9の次数=0
となるので、求める次数=6・・・(答)となります。定数項は7c3+9・・・(答)となります。
今回は多項式の定義について解説した後、多項式の項・次数・係数・定数項など必ず覚えておきべき用語をご紹介しました。
繰り返しになりますが、本記事でご紹介した用語を理解しておかないと今後の高校数学の問題を解くのが難しくなります。序盤でつまずかないためにも、必ずマスターしておきましょう。

