本記事では高校数学の数学1で学習する「命題と条件」を取り上げます。
命題と条件は共通テストでも頻出の分野で、命題と条件の後に登場する必要条件・十分条件でも活用するので、必ず理解しておきましょう。
今回は早稲田大学教育学部数学科を卒業した筆者が、命題と条件とは何かについて解説した後、真や偽とは何か、問題を解くコツなどについてわかりやすく解説していきます。
命題と条件とは?真・偽とは?わかりやすく解説
まずは命題と条件とは何かについてわかりやすく解説します。
命題とは、正しいか正しくないかが明確に決まる事柄(文章や式)のことを言います。
例えば、「100は60よりも大きい数である」という事柄は正しいので命題であると言えます。
しかし、「1万は大きい数である」という事柄は正しいか正しくないかが明確に決まらないので命題とは言えません。何に対して大きいのか?が判断できないからです。
命題が正しいとき、その命題は真であるといい、命題が正しくないとき、その命題は偽であるといいます。
命題は真または偽どちらかが必ず決まります。
そして、文字(xやaなど)を含んだ文や式においては文字の値によって真偽が変わる場合があります。
例えば、「xは自然数である」という文はx=10のときは真ですが、x=-5のときは偽となります。
このように、文字(今回はx)を含んだ文や式の事をxに関する条件といいます。
2つの条件p、qについて、命題「pならばq」をp⇒qと書きます。
そして、pをこの命題の仮定、qをこの命題の結論といいます。
また、「pならばqかつ、qならばp」をp⇔qと書きます。
例えば、「x=0 ⇒ xy=0」という命題があったとします(x、yは実数とする)この命題の真偽を考えてみましょう。
※実数がわからない人は実数とは何かについて解説した記事をご覧ください。
この場合、x=0が仮定、xy=0が結論に該当します。
x=0のとき、0であるxにどんな数をかけても0になるので、x=0のとき、xy=0になります。
よって、この命題は真となります。
では、「x2=16 ⇒ x=4」という命題の真偽はどうでしょうか?
16の平方根は4だけでなく-4もあるので、この命題は偽となります。
※平方根がわからない人は平方根とは何かについて解説した記事をご覧ください。
命題と条件の問題を解くコツ
命題と条件の問題を解くコツとしては、以下を覚えておくことです。
- 命題が偽である=反例を1つでも示せれば良い
- 命題が真である=真であることを証明する
とある命題が与えられたとき、反例を1つでも示すことができればその命題は必ず偽となります。
逆に、命題が真である場合、真であることを証明する必要があります。
なので、命題の真偽を答える問題では、まずは反例がなさそうかを疑うのが良いでしょう。
反例がなさそうであればその命題は真である可能性が高いので、真であることの証明ができないかを考えましょう。
真であることの証明をするためには、以下のコツがあります。
- 例:5の倍数=5kとおく(kは自然数)
- 偶数=2nとおく(nは自然数)
- 奇数=2n+1とおく(nは自然数)
命題と条件の問題では「〇〇が××の倍数であるとき」や「〇〇が偶数(奇数)のとき」などの仮定が頻出です。
例えば、「mが9の倍数であるとき」と言われたらm=9kとおきます(kは自然数)
「mが7の倍数であるとき」ならm=7k(kは自然数)です。
「mが偶数であるとき」と言われたらm=2n(nは自然数)とおきます。奇数なら2n+1です。
このような置き換えを行うと、命題が真であることの証明がスムーズに進む場合が多いです。コツ・テクニックの1つとして覚えておきましょう。
条件と集合の関係
2つの条件pとqを満たすものの全体の集合をそれぞれP、Qとし、命題「p⇒q」が真であるとき、P⊂Qがなりたちます。
※記号「⊂」の意味については集合の記号一覧と読み方を解説した記事をご覧ください。
逆に、P⊂Qであるならば命題「p⇒q」は真となります。
例えば、命題「0<x<1 ⇒ |x|<2」の真偽を考えてみましょう。
|x|<2=-2<x<2より、上記の命題は「0<x<1 ⇒ -2<x<2」と書き換えることができます。
0<x<1と-2<x<2を数直線上に表してみると以下の通りとなり、-2<x<2の中に0<x<1が含まれていることがわかります。
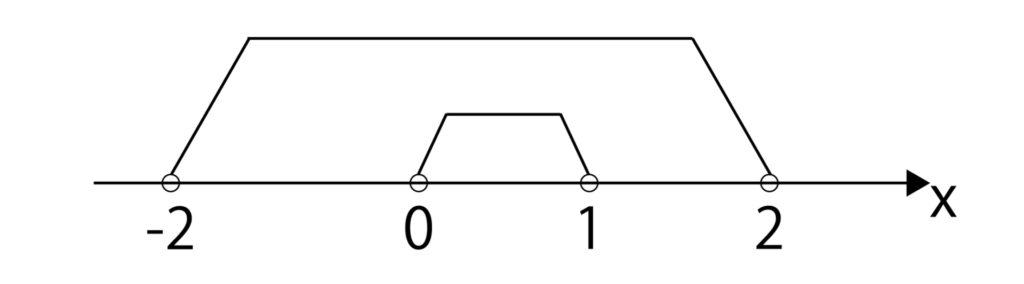
※上記の図において、数字の上にある◯の意味がわからない人は一次不等式とは何かについて解説した記事をご覧ください。
よって、命題「0<x<1 ⇒ |x|<2」は真となります。
命題と条件の練習問題
最後に命題と条件の練習問題を用意しました。
命題と条件の練習問題は上記のような解説文だけだとなかなかイメージがつかないので、たくさんの練習問題を解いて慣れることが重要です。
【練習問題1】
以下の命題の真偽を答えなさい。
(1)x2=y2ならば、x=yである。ただし、x、yは実数とする。
(2)nが8の倍数ならば、nは4の倍数である。ただし、nは自然数とする。
(3)m+nが偶数ならば、n、mはともに偶数である。ただし、mとnは自然数とする。
【解答&解説】
(1)x=2、y=-2の場合、x2=4、y2=4となりますが、x=yではありません。よって命題は偽となります。
※上記でも解説した通り、反例が1つでも見つかればその命題は偽となります。
(2)nが8の倍数であるとき、nは自然数kを用いて8kと表すことができます。
このとき、n=8k=4×2kとなり、2kは自然数なので、nは4倍数となります。よって命題は真となります。
※命題が真である場合は真であることを証明しましょう。
(3)m=5、n=9のとき、m+n=14で偶数ですが、n=奇数、m=奇数です。よって、命題は偽となります。
【練習問題2】
集合を利用して以下の命題の真偽を答えなさい。
「|x|<2ならば、-3<x<3である」
※xは実数とする。
【解答&解説】
|x|<2=-2<x<2より、命題は「-2<x<2ならば、-3<x<3である」と書き換えることができます。
-2<x<2と-3<x<3を数直線上に表すと以下のようになります。
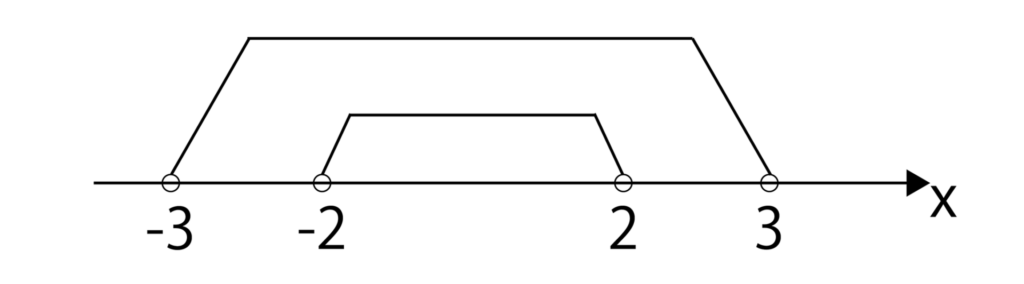
-3<x<3の中に-2<x<2が含まれているので、命題は真となります。
いかがでしたでしょうか?
今回は命題と条件とは何かについて解説した後、命題と条件の問題を解くコツや集合との関係などについて解説しました。
繰り返しにはなりますが、数学1でこの後に学習する必要条件・十分条件でも命題と条件は登場するので、今のうちに必ず理解しておきましょう。
必要条件・十分条件とは何かについて解説した記事もご用意していますので、ぜひ合わせてご覧ください。


