中学数学では比例と一緒に反比例も学習します。後ほど詳しく解説しますが、反比例は比例の対義語だと理解して問題ありません。
比例も反比例も中学数学の中でかなり重要な分野なので、必ず理解しておきましょう。
今回は早稲田大学教育学部数学科を卒業した筆者が反比例の意味や反比例で使える公式・グラフの書き方などについてわかりやすく解説します。
最後には反比例に関する練習問題も用意しているので、ぜひ最後までご覧ください。
反比例とは?わかりやすく解説
まずは反比例とは何かについて具体例でわかりやすく解説します。
反比例とは、変数xとyがあったときxが2倍、3倍、4倍・・・になるにつれてyの値が1/2倍、1/3倍、1/4倍・・・となることです。
※変数が何かわからない人は変数とは何かについて解説した記事をご覧ください。
ちなみにですが、比例とは変数xとyがあったときxが2倍、3倍、4倍・・・になるにつれてyの値が2倍、3倍、4倍・・・となることでした。なので、反比例は比例の反対のような用語であると認識していただいて問題ありません。
※比例とは何かについて解説した記事もぜひ合わせてご覧ください。
反比例の式
では、反比例の式はどうやって表すことができるのでしょうか?
結論から申しますと、反比例の式はy=a/xと表すことができます(ただし、aは0ではないとする)
※比例の式はy=axでしたね。
反比例の式y=a/xにおいて、aのことを比例定数といいます。比例定数という言葉は比例の式でも登場しましたが、反比例でも使います。
※詳しくは比例定数とは何かについて解説した記事をご覧ください。
例えば、y=10xという反比例の式を考えてみましょう。
- x=1のときy=10
- x=2のときy=5
- x=4のときy=2.5
- x=10のときy=1
ですね。xの値が1から2に変化(=2倍)したとき、yの値は10から5になっているので1/2倍になっていることが確認できます。
また、xの値が2から10に変化(=5倍)したとき、yの値は5から1になっているので1/5倍になっていることが確認できます。
先ほど解説した通り、xが2倍、3倍、4倍・・・になるにつれてyの値が2倍、3倍、4倍・・・になっていることが確認できましたね。
反比例の式y=a/xは必ず頭に入れておきましょう。
aは必ずしも正の数である必要はありません。負の数でもOKです。
※正の数・負の数とは何かについて解説した記事もぜひあわせてご覧ください。
反比例の比例定数aの求め方
では、先ほど解説した反比例の比例定数aがわからない場合はどうやって求めれば良いのでしょうか?
例題で解説していきます。
【例題】
(1)10kmの道のりをx[km/時]で走るときにかかる時間をy[時間]としたとき、比例定数を求めなさい。
(2)yがxに反比例し、x=4のときy=-8である。このとき、比例定数を求めなさい。
【解答&解説】
(1)まず1つ目は、文章から反比例の式を作って比例定数を求めるパターンです。
時間=道のり/速さで求めることができるのでした。
なので、y=12/xが成り立ちます。よって比例定数=12・・・(答)となります。
(2)反比例の式y=a/xを変形すると、a=xyとなりますね。
※xyはxとyの掛け算のことでした。詳しくは文字と式について解説した記事をご覧ください。
つまり、yがxに反比例するとき、比例定数はxyで求めることができます。
よって比例定数=4×(-8)=-32・・・(答)となります。
【別解】
yがxに反比例することから、aを比例定数とするとy=a/xと表すことができます。
x=4のときy=-8なので、-8=a/4が成り立つことから、比例定数a=-32となります。
反比例のグラフの書き方
ここからは反比例のグラフを書いてみましょう。難しくないのでご安心ください。
※比例のグラフの書き方について解説した記事もぜひ合わせてご覧ください。
今回はy=10/xのグラフを書いてみます。
反比例のグラフの書き方は以下の4ステップです。
- xy座標を書く
- y=10/xが通る点を2つ書く
- 2点を通る双曲線を書く
- 原点Oを対称にして双曲線を書く
順番に詳しく解説していきます。
xy座標を書く
比例のグラフを書くときもまずはxy座標を書きました。反比例のときも同じく、まずはxy座標を書きましょう。
y=10/xが通る点を2つ書く
次はy=10/xが通る点をまずは2つ書きましょう。
書き方のポイントは2つあります。
まず1つ目のポイントは反比例の比例定数に注目して、xとyがともに整数になるような点を考えましょう(その方が計算が楽ですよ)
※比例定数aの値によってはどうしてもx、yが分数になってしまうケースもありますが、その場合はそれでもOKです。
今回は比例定数=10なので、xが10の約数だとx、yはともに整数になりそうですね。
今回は点(2、5)と(5、2)としてみます。
そして、2つ目のポイントは2つの点が同じ象限にあるようにすることです。
今回の(2、5)と(5、2)はともに第1象限にありますね。
※象限がわからない人はxy座標とは何かについて解説した記事をご覧ください。
では、以下のようにxy座標上に(2、5)と(5、2)を記載しましょう。
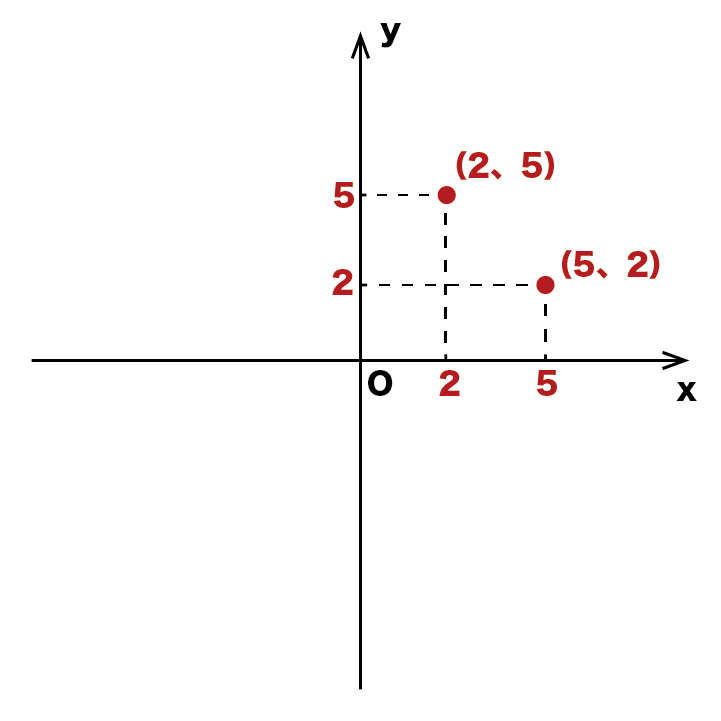
2点を通る双曲線を書く
次は(2、5)と(5、2)を通るようになめらかな曲線を書きます。この曲線のことを双曲線というので覚えておきましょう。
反比例y=a/xのグラフは必ずなめらかな双曲線になります。
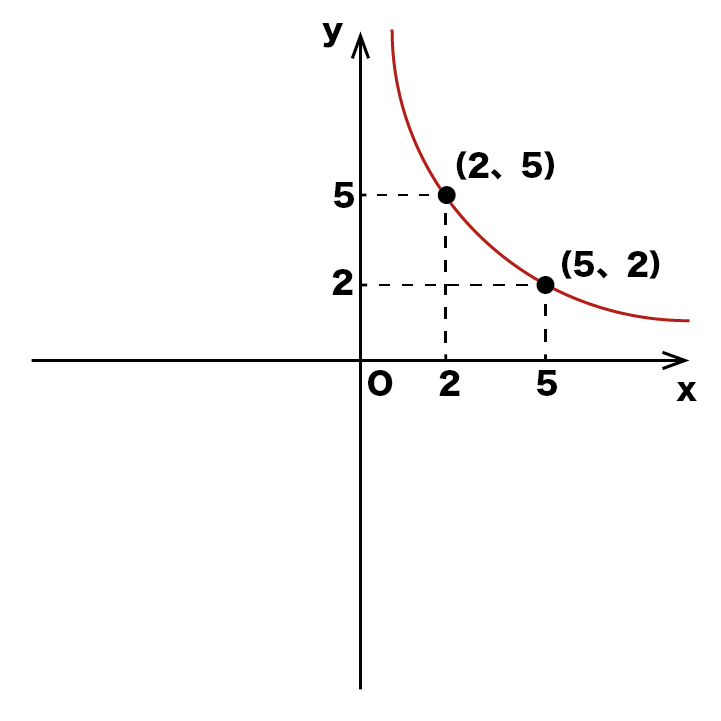
双曲線を書くときの注意点ですが、双曲線はx軸、y軸と交わることはありませんのでご注意ください(後ほど詳しく解説します)
原点Oを対称にして双曲線を書く
いよいよ最後のステップです。
反比例のグラフは必ず双曲線が2つ存在します。先ほど1つの双曲線を書けたので、残りもう1つの双曲線を書きます。
反比例の式y=10/xにおいて、xの値が負のとき、yの値も負になりますね。
つまり、y=10/xは(-2、-5)と(-5、-2)も通ります。
なので、先ほどと同様にxy座標上に(-2、-5)と(-5、-2)を書き、その2点を通るように以下のような双曲線を書きましょう。
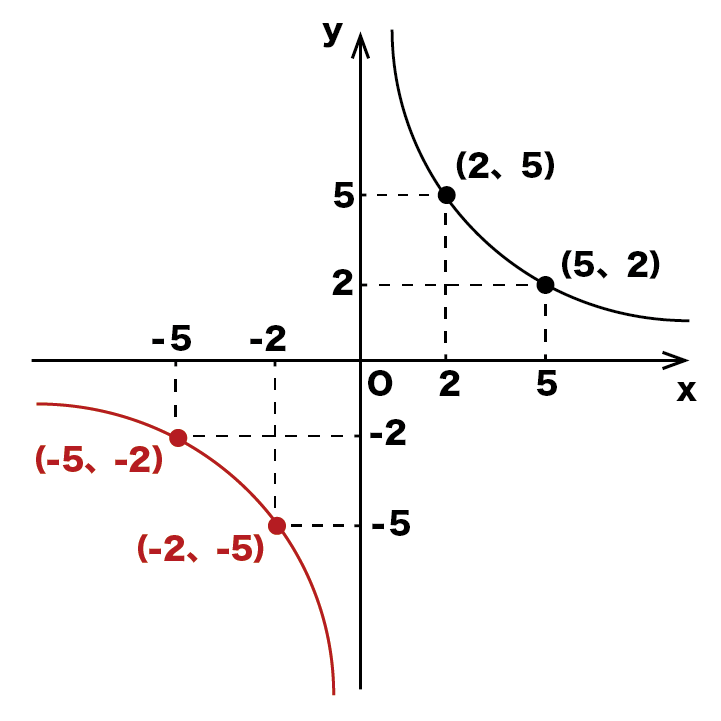
これでy=10/xのグラフは完成です。
反比例のグラフにおける2つの双曲線は原点Oで対称になります(後ほど解説します)
今回は比例定数=10が正の数なので、双曲線は第1象限と第3象限に出現しましたが、比例定数が負の数の場合は第2象限と第4象限に出現します。
気になる方は自分で比例定数が負の数である反比例のグラフを自力で書いてみましょう。
反比例のグラフの特徴
以上で反比例のグラフを書いてみましたが、ここからは反比例のグラフの特徴を3つご紹介します。
1つ目は反比例のグラフにおいて双曲線は必ず2つあるということです。
比例のグラフでは直線のグラフが1つしかありませんでしたが、反比例では2つの双曲線が登場するので、1つだけ書いてもう1つを書き忘れることがないようにしましょう。
2つ目の特徴は双曲線はx軸、y軸とは交わらないということです。
反比例の式y=a/x(aは0でないとする)において、x=0の場合、分母が0になるのでa/xは計算不可となります(数学においては分母が0になることはあり得ません)
x=0になることがあり得ないので、反比例のグラフがy軸と交わる(x=0になる)ことはありません。
xもaも0ではない限り、yが0になることはないので反比例のグラフはx軸とも交わる(y=0になる)ことはありません。
反比例のグラフの3つ目の特徴は2つの双曲線は原点Oで対称になるということです。
これは簡単にいうと1つの双曲線が点(p、q)を通るとき、もう1つの双曲線は点(-p、-q)を必ず通るということです(x座標とy座標の符号が逆になります)
先ほ反比例y=10/xのグラフを書きましたが、2つの双曲線は
- 第1象限では(2、5)と(5、2)を通る
- 第3象限では(-2、-5)と(-5、-2)を通る
ことがわかりましたね。(2、5)と(-2、-5)、(5、2)と(-5、-2)において符号が逆になっていることがわかります。
これも非常に重要な反比例のグラフの特徴ですが、教科書ではあまり取り上げられていないので、ぜひ知っておきましょう。
反比例の練習問題
最後に反比例の練習問題をご用意しました。
すべて基本的な問題なので、全問正解できるまで反比例を理解しましょう。
【問題1】
yがxに反比例し、以下のとき、yをxの式で表現しなさい。
(1)比例定数が-5
(2)x=4のときy=12
(3)x=-12のときy=-3
【解答&解説】
(1)y=-5/x
(2)y=a/xにx=4、y=12を代入すると、12=a/4となるので、a=48となります。
よって、y=48/x・・・(答)となります。
(3)y=a/xにx=-12、y=-3を代入すると、-3=-a/12となるので、a=36となります。
よって、y=36/x・・・(答)となります。
【問題2】
yがxに反比例し、x=-8のときy=3であることがわかっている。
(1)x=5のとき、yの値を求めよ。
(2)y=-6のとき、xの値を求めよ。
【解答&解説】
(1)y=a/xにx=-8、y=3を代入すると、3=-a/8となるので、a=-24となります。
よって、y=-24/xであることがわかりました。
したがって、x=5のときy=-24/5・・・(答)となります。
(2)y=-24/xにy=-6を代入しましょう。
-6=-24/xより、x=4・・・(答)であることがわかりました。
いかがでしたか?
今回は反比例の意味について解説した後、反比例の公式やグラフの書き方、特徴などについて解説していきました。
学習することが多かったかもしれませんが、1つずつで良いのでしっかりと内容を理解していくことが重要です。焦らず勉強を進めていきましょう!