今回は文字と式を取り上げます。後ほど詳しく解説しますが、文字とはaやbやc、x、yなどのことです。
文字と式を学習することによって式を綺麗に書けたりすることが可能になります。
この先の高校数学でも必ず使うので、しっかりと頭に入れておきましょう。
本記事では早稲田大学教育学部数学科を卒業した筆者が文字と式について中1・小6でもわかるように例を使いながら解説します。
また、解き方だけでなく文章題の例題を用意しているので、ぜひ最後までお読みください。
文字と式とは?中1・小6でもわかるように解説
まずは文字と式とは何かについて解説します。
文字とは冒頭でも解説した通りaやbやc、x、yなどのことです。
そして、文字を使った式のことを文字式と言います。
中学数学からは様々な数量や式を文字を使って表現する機会が増えていきます。
文字式には以下のルールがあるので、しっかりと覚えておきましょう。
掛け算の記号「×」は省略する
1つ目のルールは掛け算の記号「×」は省略するということです。
例えば、5×aは5a、a×b×cはabcと表現します。
ちなみにですが、5aとa5と書くことはほとんどありません。数字→文字の順番で記載するのが一般的です。
そして、abcのようにアルファベットが続く場合はアルファベット順に記載するのが一般的です。
同じ文字の積は累乗を使う
乗法について学んだとき、累乗という言葉が出てきましたね。
※累乗が何かわからない人は乗法とは何かについて解説した記事をご覧ください。
例えば、5×5×5は53と表現するのでした。
同じ文字を掛け算するときも同様です。例えばa×a×aはa3と表現します。
文字にかけられた数が-1や1のとき、記号「-」は書かない
先ほどご紹介した1つ目のルールに則ると、例えば1×a=1aと表現したいところですが、1aはaと表現します。1は省略するのです。
また、-1×yは-1yと表現したいところですが、これも1は省略して-yと表現します。
-1×a×bは-abと表現します。
ただし、例えば0.1×aは0.1aなのでご注意ください(0.1は1ではないからです)
以上が文字式のルールとなります。これはルールであり既に決められたことなので「なぜそうなるのか?」については証明のしようがありません。
文字式のルールとしてしっかりと頭に入れておきましょう。
文字式と除法
文字式においては除法の記号「÷」は使わずに分数の形で表現します。
※除法がわからない人は除法とは何かについて解説した記事をご覧ください。
例えば、a÷3はa×1/3なので、a/3となります。
ちなみにですが、例えばa÷3/5はa×5/3なので、5a/3と表現しますが、帯分数を使って1と2a/3と書いてはいけません。
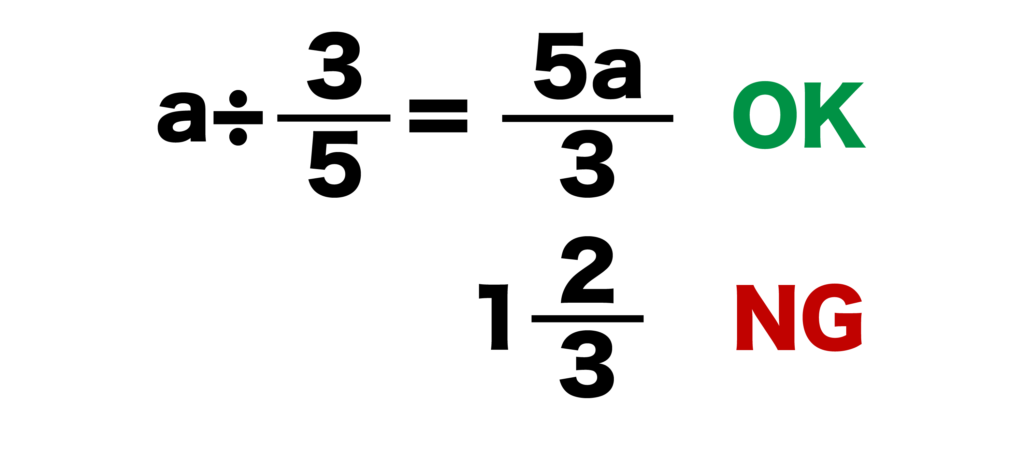
中学数学以降では帯分数は基本的に使わないのでご注意ください。
また、上記で解説した通り乗法と除法においては記号「×」も「÷」も省略しましが、加法や減法(「+」と「-」)は省略しません。
例えば、a+bをabなどと省略することはできません。
※加法と減法とは何かについて解説した記事もぜひ合わせてご覧ください。
文字式と代入
文字式を使えるようになることで、様々な数量を文字式で表現することが可能になります。
例えば、1個200円のお菓子をa個買った場合の料金は200×a=200a[円]となります。
単位が存在するときは単位を付けるように心がけましょう。
また、文字式の文字にある数をあてはめることを代入(だいにゅう)と言います。
そして、代入して計算した結果のことを式の値と言います。
例えば、50xにx=4を代入すると50×4=200となりますね。200が式の値となります。
文字と式の練習問題
では文字と式に関する練習問題を解きましょう。
以上で学習したルールを覚えるチャンスだと思って解いてみてください。
【問題】
以下の式を「×」や「÷」を除いた式で表しなさい。
(1)a×6
(2)0.5×c×a
(3)y×y×5×z×z×z
(4)(a+b)×(a+b)
(5)x÷y
(6)x÷(-10)
(7)5÷a÷b
(8)(p+q)÷7
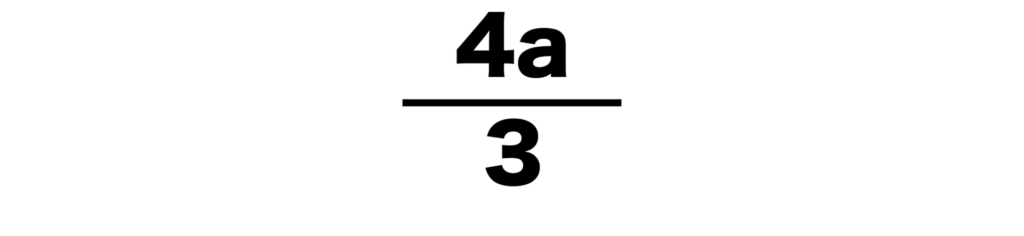
(9)a÷3/4
(10)a÷(b-c)
【解答&解説】
(1)a×6=6a
(2)0.5×c×a=0.5ac
(3)y×y×5×z×z×z=5y2z3
(4)(a+b)×(a+b)=(a+b)2
(5)x÷y=x/y
(6)x÷(-10)=-x/10
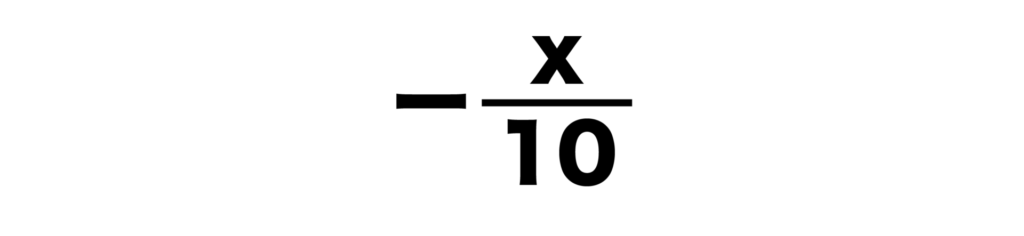
(7)5÷a÷b=5/a × 1/b=5/ab

(8)(p+q)÷7=p+q/7

(9)a÷3/4=a×4/3=4a/3
(10)a÷(b-c)=a/b-c
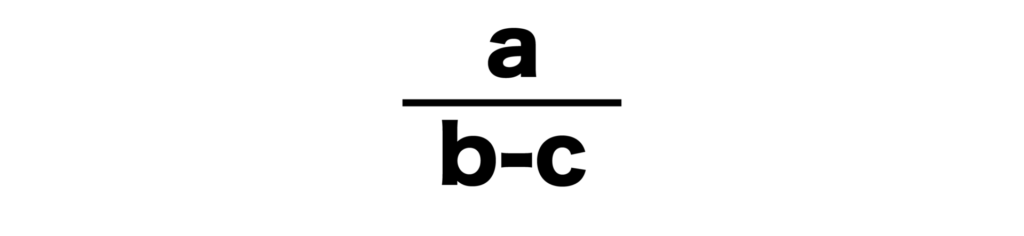
文字と式と文章問題
次は上記で学習したことをもとに文字と式を利用した文章問題を解いてみましょう。
【文章問題1】
A君は1本a円の鉛筆を8本と1個b円の消しゴムを2個買った。
(1)このとき、料金の合計を文字式で表しなさい。
(2)鉛筆1本の値段が100円、消しゴム1個の値段が150円のとき、料金の合計はいくらになるか求めなさい。
【解答&解説】
(1)a×8+b×2=8a+2b[円]
(2)a=100、b=150を8a+2bに代入して、
8×100+2×150=800+300=1100[円]・・・(答)となります。
【文章問題2】
Pcmのリボンがある。このリボンからQcmのリボンを3本切り取る。
(1)このとき、残りのリボンの長さを文字式で表しなさい。
(2)Q=5のとき、残りのリボンの長さは150cmとなった。このとき、Pの値を求めよ。
【解答&解説】
(1)P-Q×3=P-3Q[cm]
(2)P-3Qが残りのリボンの長さを表しており、P-3QにQ=5を代入するとP-3×5=P-15[cm]となりますね。
これが150cmなので、P-15=150となりますね。つまり、P=150+15=165[cm]・・・(答)となります。
いかがでしたか?今回は文字と式を中1・小6でもわかるように解説していきました。
文字と式は数学の基礎となる部分です。この先もずっと登場するので、必ず使いこなせるようにしておきましょう。


