後ほど詳しく解説しますが、乗法(じょうほう)とは簡単にいうと掛け算のことです。
中学に入ると、正の数と負の数を序盤で学びますが、正の数と負の数を組み合わせた乗法は数学において基礎中の基礎なので、必ず理解しておく必要があります。
※正の数・負の数とは何かについて解説した記事もぜひ合わせてご覧ください。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が乗法とは何かについて解説した後、正の数・負の数が混じった乗法のやり方についてわかりやすく解説していきます。
最後には乗法の練習問題も用意しているので、ぜひ最後までお読みください。
乗法とは?
まずは乗法とは何かについて解説していきます。
冒頭でも解説した通り、乗法とは掛け算のことです。掛け算は小学校でも学習しましたね。
2×5=10や7×3=21などのことです。これらも立派な乗法です。
乗法の結果のことを積(せき)と言います。例えば、2×5=10なので「2×5の積は10である」と言えるわけです。
小学校のときの乗法と中学数学での乗法で違うポイントは負の数(=マイナスの数)があるかどうかです。
小学校の乗法では正の数×正の数しか登場しませんでしたが、中学数学では
- 正の数×負の数
- 負の数×負の数
というパターンが登場します。
※ちなみにですが、足し算のことは加法、引き算のことは減法と言います。加法と減法について詳しく解説した記事もぜひ合わせてご覧ください。
乗法の計算のやり方
ここからは正の数と負の数が混じった乗法の計算のやり方について解説していきます。
中学数学の基礎となる内容なので必ず理解しておきましょう。
正の数×正の数
まずは小学校でも学習した正の数×正の数の乗法について復習しておきます。
例えば、3×2を考えてみましょう。3×2は(+3)×(+2)のことですね。
(+3)×(+2)は原点から+3と同じ方向に2倍するという意味です。
以下のように数直線で考えると、(+3)×(+2)=+6であることがわかります。
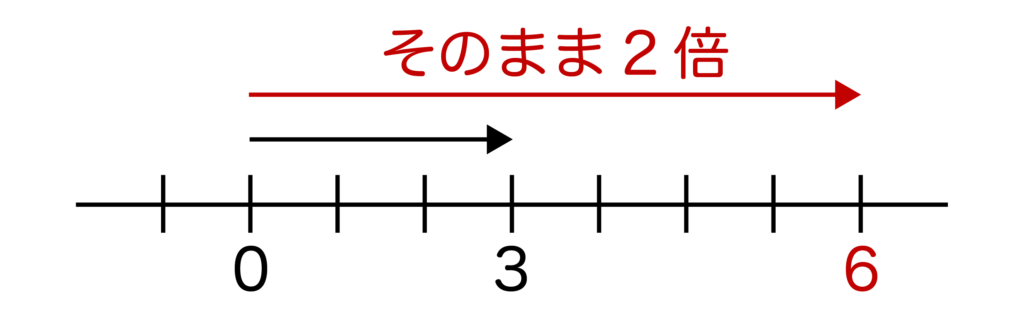
乗法に関してはまずはこの考え方をしっかりと抑えておきましょう。
負の数×正の数
次は負の数×正の数の乗法を考えていきましょう。
例として(-2)×3を計算してみます。(-2)×3は(-2)×(+3)のことですね。
先ほどの考え方に沿うと、原点から-2と同じ方向に3倍するということになりますね。
よって、以下のように数直線で考えると、(-2)×3=-6となるわけです。
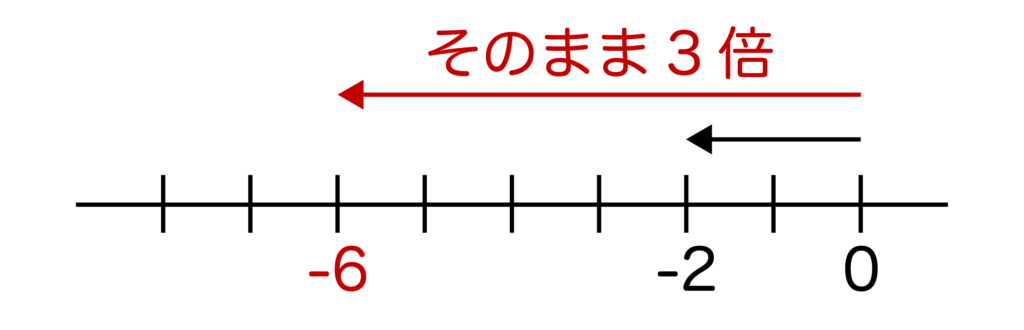
正の数×負の数
続いては正の数×負の数の乗法です。
例として3×(-2)を計算してみます。
負の数を掛ける=数直線上では掛けられる数(=今回の場合は3)の符号と反対の向きに拡大することです。
つまり、3×(-2)は原点から+3と反対の方向に2倍するということなので、以下のように数直線で考えると3×(-2)=-6であることがわかります。
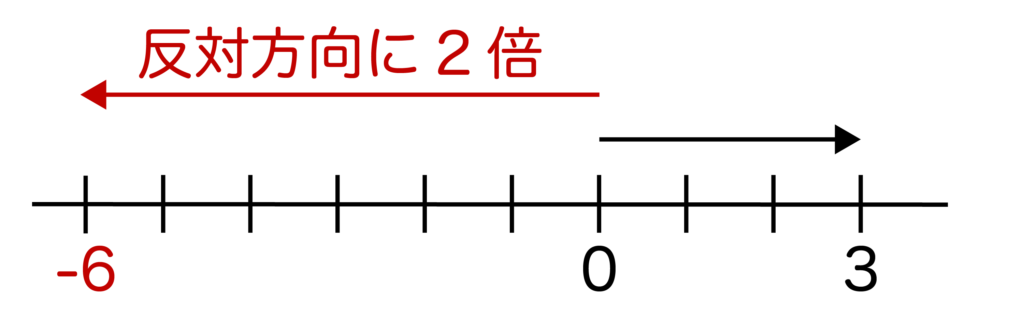
負の数×負の数
最後は負の数×負の数の乗法です。
例として(-2)×(-3)を計算します。
先ほど解説した通り、(-2)×(-3)は原点から-2と反対の方向に3倍することなので、以下のように数直線で考えると(-2)×(-3)=6となります。
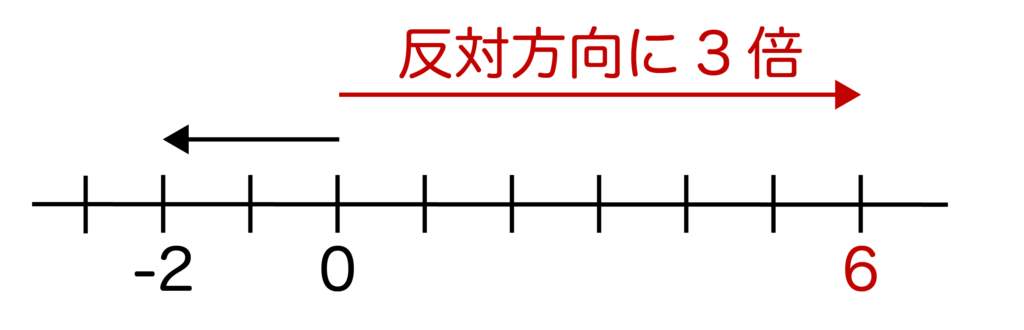
乗法の計算で必ず覚えておくべき符号の法則
以上で乗法の計算のやり方について解説しましたが、同じ符号の積は正、違う符号の積は負になっている法則に気づきましたでしょうか?以下のように
- 正の数×正の数=正の数
- 負の数×正の数=負の数
- 正の数×負の数=負の数
- 負の数×負の数=正の数
になっています。
以上のことがしっかりと頭に入っていれば正負の数が混じった乗法は何も難しくありません。
2つの数の絶対値を計算して、上記に基づいて符号を付けるだけで良いのです。
3つ以上の数の乗法
以上では2つの数の乗法について解説していきました。
ここからは、3つ以上の数の乗法について学習しましょう。
例として、(-2)×5×(-3)を計算してみます。
まず、(-2)×5を計算してみましょう。
先ほど学習した通り、負の数×正の数=負の数なので(-2)×5=-10ですね。
よって、(-2)×5×(-3)=-10×(-3)となります。
では、-10×(-3)はどうなるでしょうか?
負の数×負の数=正の数なので、-10×(-3)=30ですね。
よって(-2)×5×(-3)=30となるわけです。
では、(-3)×4×5はどうなるでしょうか?
まずは(-3)×4を計算します。(-3)×4=-12ですね。
そして、-12×5=-60ですね。よって、(-3)×4×5=-60となるわけです。
すると、以下の法則が見えてきます。
- 負の数=偶数個ならば、積は正の数
- 負の数=奇数個ならば、積は負の数
3つ以上の数の乗法においては、必ず以上の法則が成り立ちます。これは必ずおきましょう。
以上のことがしっかりと頭に入っていれば、3つ以上の数の乗法は何も怖くありません。
負の数の個数を数えて答えの符号を確定し、絶対値の計算をすれば良いだけです。
例えば、(-3)×4×(-7)×(-2)を計算する場合、負の数は3個(=奇数個)あるので答えは負の数になります。
そして、絶対値である3と4と7と2を掛け算すると168になるので、答えは-168となります。
乗法と除法の関係
冒頭で割り算のことを乗法と言うことを学びましたが、割り算のことは除法(じょほう)と言います。
※除法について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
割り算は逆数を使って掛け算に変換できるのでした。
※例えば、6÷2は6×1/2のように掛け算に変換できます。
なので、乗法の計算に除法が混じっても、以上で解説した通り
- 負の数=偶数個ならば、積は正の数
- 負の数=奇数個ならば、積は負の数
は何も変わりません。除法があっても、負の数の個数から答えの符号を確定し、絶対値の計算をするだけです。
例えば、(-3)×4×6÷(-2)を計算してみましょう。
負の数は全部で2個(=偶数個)あるので、答えは正の数になります。
あとは絶対値だけを考えた3×4×6÷2を計算すると36になるので、答えは36となります。
乗法と累乗の関係
中学数学では累乗という用語が登場します。
累乗はこの先、高校数学でも必ず登場するので必ず理解しておきましょう。
例えば、2×2×2のように同じ数をいくつか掛け合わすとき、23と書いて「2の3乗(じょう)」と読みます。
この表し方のことを累乗と言います。
例えば、42=4×4、103=10×10×10を表しています。
なので、例えば(-2)5を考えるとき、(-2)5は(-2)を5回掛けることを意味しているので、負の数である-2が5個登場することになります。
先ほどの通り、乗法においては
- 負の数=偶数個ならば、積は正の数
- 負の数=奇数個ならば、積は負の数
なので、(-2)5は負の数であることがわかります。
あとは-2の絶対値である2を5回掛けて、32となるので、(-2)5=-32となります。
ちなみにですが、(-2)5と25は全く意味が違うのでご注意ください。
(-2)5は-2を5回掛けることを意味しており、結果は-32になりますが、25は2を5回掛けることを意味しており、結果は32になります。
乗法の交換法則・結合法則・分配法則
乗法では乗法の交換法則・結合法則・分配法則の3つの法則があります。
小学校でも学習した内容ですが、念のため取り上げておきます。
交換法則
乗法の交換法則とは掛ける順番を入れ替えても結果は同じになるということです。
つまり、A×B=B×Aということです。
正の数と負の数が混じっても交換法則は成り立ちます。
例えば、4×(-8)=-32ですが、(-8)×4も-32になります。
結合法則
乗法の結合法則はどんな順番で掛け算をしても結果は同じということです。
(A×B)×C=A×(B×C)となります。
例えば、4×8×(-3)は4と8を先に掛けて、32×(-3)=-96としても問題ありませんし、8と(-3)を先に掛けて-24としてから4×(-24)=-96としても問題ありません。
ちなみにですが、AとCを先に掛けて、後からBを掛けても問題ありません。
4×8×(-3)の場合だと、4×(-3)=-12を先に求めてから8×(-12)=-96としても結果は変わりません。
分配法則
分配法則とは、(A+B)×C=A×B+A×Cが成り立つことです。
例えば、(2+5)×(-4)=7×(-4)=-28ですが、分配法則を使って、
2×(-4)+5×(-4)=-8+(-20)=-28としても結果は同じになります。
乗法の計算問題
最後に、乗法の計算問題をご用意しました。
たくさんの計算問題を解くことで乗法に慣れていくので、本記事の問題だけでなく、数学の教科書や参考書なども使ってたくさんの問題を解いてみてください。
【問題】
以下の計算をしなさい。
(1)4×(-9)
(2)(-6)×7
(3)(-23)×(-2)
(4)(-20)×(-8)×(-3)
(5)10×(-3)×(-5)
(6)53
(7)(-5)3
【解答&解説】
(1)4×(-9)=-36
(2)(-6)×7=-42
(3)(-23)×(-2)=46
(4)(-20)×(-8)×(-3)=160×(-3)=-480
※負の数が3つ(=奇数個)あるので答えは負の数になります。
(5)10×(-3)×(-5)=-30×(-5)=150
※負の数が2つ(=偶数個)あるので答えは正の数になります。
(6)53=5×5×5=125
(7)(-5)3=(-5)×(-5)×(-5)=-125
いかがでしたか?今回は乗法とは何かについて解説していきました。
正負の数がどれだけ入っても、必ず負の数の個数に注目するようにしましょう。
負の数が奇数個であれば答えは負の数、負の数が偶数個であれば答えは正の数です!


