三角形の相似条件と相似比・面積比の関係についてわかりやすく解説！

三角形の相似条件や相似比・面積比の関係は中学数学が習いますが、高校数学の数学Aの教科書や参考書でも中学数学の復習として取り上げているケースもあります。

本記事でも念の為、中学数学の復習として三角形の相似条件と相似比・面積比を取り上げておきます。

今回は早稲田大学教育学部数学科を卒業した筆者が三角形の相似条件と相似比・面積比の関係について図解でわかりやすく解説していきます。

三角形の相似条件や相似比・面積比の関係は図形の基礎知識でもあるので、必ず理解しておきましょう。

相似・相似条件・相似比・面積比とは？

三角形の相似条件について解説する前に、まずは相似・相似条件・相似比・面積比とは何かについて解説します。

相似とは簡単にいうと「形が同じである」ということです。

例えば、以下の図のようにAB＝5、AC＝4、BC＝7の三角形ABCとAB＝10、AC＝8、BC＝14の三角形DEFがあるとします。

※∠A、∠B、∠Cの大きさはともに同じです。

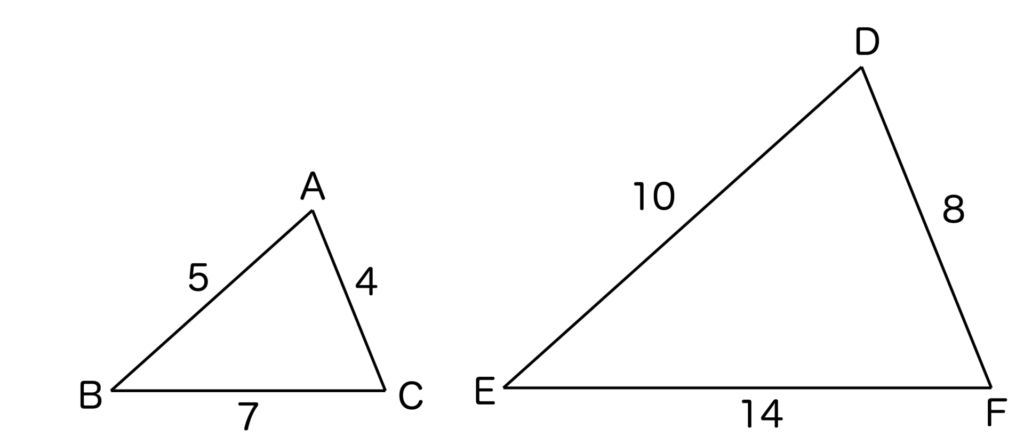
この場合、∠A、∠B、∠Cの大きさはともに同じなので、三角形DEFは三角形ABCと形は同じで、三角形DEFは三角形ABCを2倍にした大きさになっていますね。

なので、三角形ABCと三角形DEFは相似であると言えます。

相似は記号「∽」を使って表すことができます。

三角形ABCと三角形DEFが相似であるとき、相似の記号「∽」を使って「三角形ABC∽三角形DEF」と表すことができます。

そして、相似条件とはその名の通り「相似になるための条件」のことです。何が成り立てば相似と言えるのか？を表したものとなります。

後ほど詳しく解説しますが、三角形の相似条件は全部で3つあります。

相似比は簡単にいうと辺の長さの比のことです。

上記の三角形ABCと三角形DEFの場合、辺の長さの比は、

• AB：DE
• AC：DF
• BC：EF

すべてにおいて1：2となっているので、三角形ABCと三角形DEFの相似比＝1：2となります。

面積比はその名の通り面積の比のことです。後ほど詳しく解説しますが、面積比は相似比の2乗になります。

したがって、上記の三角形ABCと三角形DEFの場合だと、相似比＝1：2なので、面積比は1²：2²＝1：4となります。

三角形の相似条件

ここからは三角形の相似条件について解説していきます。

先ほども解説した通り、三角形の相似条件は以下の通り全部で3つあります。

• 3組の辺の比がすべて等しい
• 2組の辺の比とその間の角がそれぞれ等しい
• 2組の角がそれぞれ等しい

三角形の相似条件は三角形の合同条件に似ており、暗記必須です。

※三角形と直角三角形の合同条件について解説した記事もぜひ合わせてご覧ください。

3組の辺の比がすべて等しい

三角形の相似条件1つ目は「3組の辺の比がすべて等しい」です。

以下の図のように辺の長さがa、b、cの三角形ABCに対して、kを正の定数として辺の長さがka、kb、kcの三角形DEFがあれば三角形ABCと三角形DEFは相似となります。

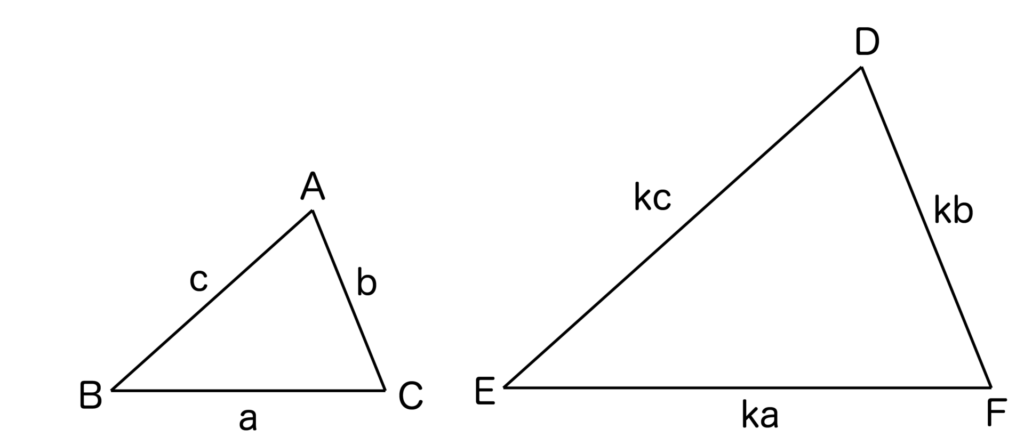
3辺すべてがk倍になっているということがポイントです。

例えば、2辺だけk倍で残りの1辺はm倍などの場合は三角形ABCと三角形DEFは相似とは言えませんのでご注意ください。

2組の辺の比とその間の角がそれぞれ等しい

三角形の相似条件2つ目は「2組の辺の比とその間の角がそれぞれ等しい」です。

以下の図のような三角形ABCに対して、∠B＝∠E、kを正の定数として辺の長さがka、kcの三角形DEFがあれば三角形ABCと三角形DEFは相似となります。

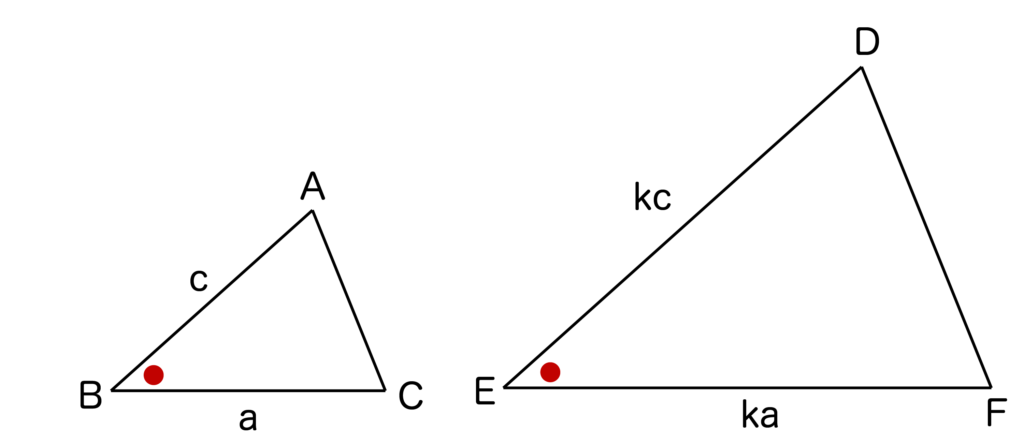
2組の辺の比と「その間の角」がそれぞれ等しいのがポイントになります。

なので、例えば∠A＝∠D、kを正の定数として辺の長さがka、kcの三角形DEFがあったとしても三角形ABCと三角形DEFは相似であるとは言えません。

∠Aはaとcの間の角ではありませんし、∠Dはkaとkcの間の角ではないからです。

2組の角がそれぞれ等しい

三角形の相似条件3つ目は「2組の角がそれぞれ等しい」です。

以下の図のような三角形ABCに対して、∠B＝∠E、∠C＝∠Fの三角形DEFがあれば三角形ABCと三角形DEFは相似となります。

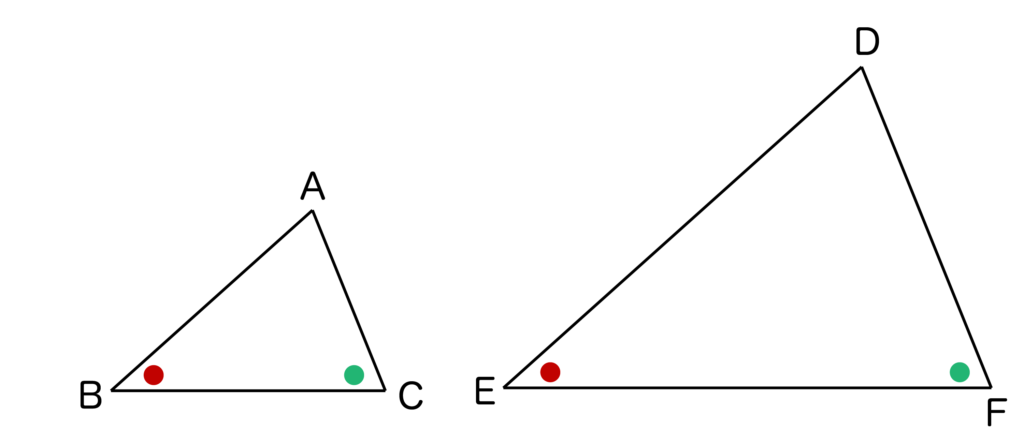
三角形の内角の和は常に180°なので、∠B＝∠E、∠C＝∠Fならば∠A＝∠Dが必然的に成り立ちます。

※三角形の内角の和が180°である理由については内角・外角とは何かについて解説した記事をご覧ください。

3つの角度の大きさが同じであれば必ず同じ形の三角形になることは想像がしやすいのではないでしょうか。

三角形の相似条件はなぜ3つ？

以上でご紹介した三角形の相似条件のうち1つでも当てはまれば2つの三角形は相似であると言えます。

では、なぜこの3つの相似条件のうち1つでも当てはまれば2つの三角形は相似であると言えるのでしょうか？

その理由に関しては、残念ながら中学数学・高校数学の教科書には載っていないことがほとんどでしょう。なぜなら、その理由を追求すると大学数学の内容になってしまうからです。

なので、中学数学・高校数学においては上記でご紹介した三角形の相似条件3つは丸暗記するしかありません。

三角形の相似条件は証明なしに使って問題ないのです。

三角形の相似条件と相似比・面積比

相似比は先ほども解説した通り、簡単にいうと辺の長さの比のことです。

以下の図のようにAB＝5、AC＝4、BC＝7の三角形ABCとAB＝10、AC＝8、BC＝14の三角形DEFがあったとき、三角形ABCと三角形DEFは3辺の比がすべて等しいので相似と言えます。

辺の比＝5：10＝1：2になっているので、相似比は1：2となるわけです。

また、面積比は面積の比のことであり、必ず相似比の2乗になります。

上記の三角形ABCと三角形DEFの相似比は1：2なので、面積比は1²：2²＝1：4となります。

なぜ面積比は相似比の2乗になる？

では、なぜ面積比は相似比の2乗になるのでしょうか？その証明を行なっていきます。

以下の図のような直角三角形ABCと直角三角形DEFがあるとします。3組の辺の比がすべて等しいので、三角形ABCと三角形DEFは相似となります。

相似比はAB：DE＝c：kc＝1：kですね（kは正の定数とします）

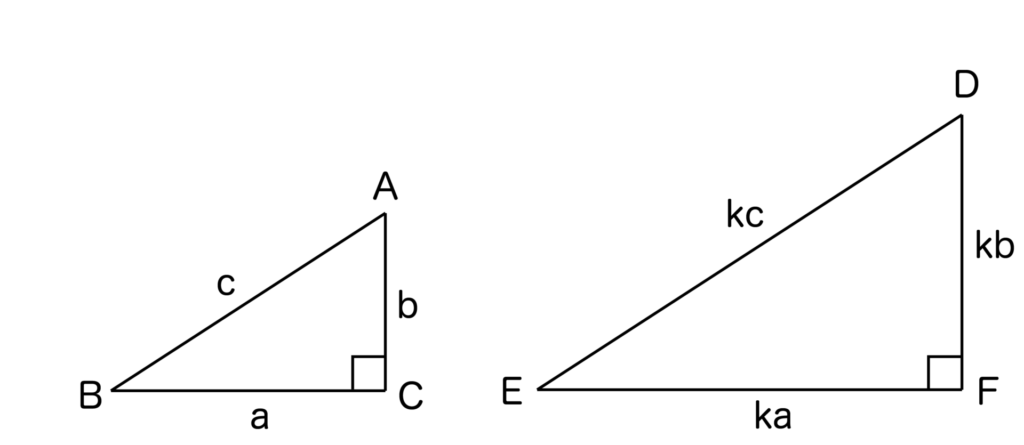
このとき、三角形ABCの面積＝a×b÷2＝ab/2、三角形DEFの面積＝ka×kb÷2＝abk²/2ですね。

よって、三角形ABCの面積：三角形DEFの面積＝ab/2：abk²/2＝1：k²です。

相似比＝1：kでしたので、面積比は相似比の2乗になっていることが証明できました。

三角形の相似条件を使った練習問題

最後に、三角形の相似条件を使った練習問題を1つ解いてみましょう。

【問題】

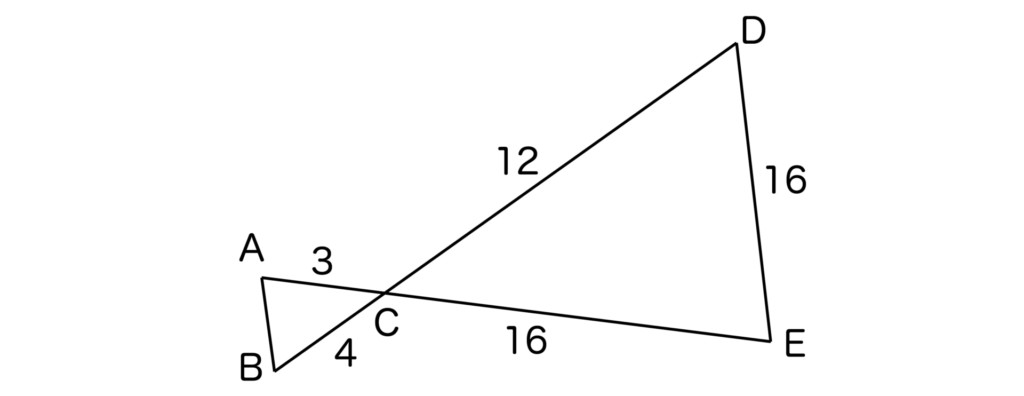
以下の図において、相似な三角形の組を見つけてABの長さを求めなさい。また、その組の相似比と面積比も求めなさい。

【解答＆解説】

三角形ABCと三角形DECにおいて、

• AC：DC＝3：12＝1：4・・・①
• BC：EC＝4：16＝1：4・・・②

対頂角は等しいので、∠ACB＝∠DCE・・・③

※対頂角がわからない人は対頂角・同位角・錯角とは何かについて解説した記事をご覧ください。

①〜③より2組の辺の比とその間の角がそれぞれ等しいので三角形ABCと三角形DECは相似となります。

よって、相似比は1：4・・・（答）となります。

面積比は1²：4²＝1：16・・・（答）です。

AB：DE＝1：4で、DE＝16なので、AB：16＝1：4より、AB＝4・・・（答）となります。

いかがでしたでしょうか？

今回は三角形の相似条件と相似比・面積比の関係について解説していきました。

三角形の相似条件は三角形の合同条件と一緒に必ず暗記しておきましょう！