三角形と直角三角形の合同条件は中学数学で学習しますが、高校数学の数学Aでも教科書によっては中学数学の復習として簡単に三角形と直角三角形の合同条件を取り上げている場合もあります。
なので、本記事でも念のため三角形と直角三角形の合同条件を取り上げておきます。
今回は早稲田大学教育学部数学科を卒業した筆者が三角形と直角三角形の合同条件について図解でわかりやすく解説していきます。
合同、合同条件とは?
三角形と直角三角形の合同条件について解説する前に、まずは合同と合同条件とは何かについて解説しておきます。
合同とは「全く同じ形」という意味です。
例えば「三角形ABCと三角形DEFは合同である」というと、三角形ABCと三角形DEFは全く同じ形をしているという意味になります。
「全く同じ」なので、1mmでも辺の長さが違っていると合同とは言えませんし、1°でも角度が違っていたりしても合同とは言えません。
そして、合同条件とはその名の通り合同になるための条件のことです。
後ほど詳しく解説しますが、三角形の合同条件は3つあります。つまり「三角形ABCと三角形DEFは合同である」と言い切るためには3つのうちのいずれかの条件を満たせば良いのです。
ちなみにですが、合同は記号「≡」を使って表すことができます。例えば「三角形ABCと三角形DEFは合同である」は三角形ABC≡三角形DEFと表現できます。
この記号は数学の基礎知識の1つなので、必ず覚えておきましょう。
三角形の合同条件
まずは三角形の合同条件からご紹介していきます。
三角形の合同条件は以下の3つです。
- 3辺がそれぞれ等しい
- 2辺とその間の角がそれぞれ等しい
- 1辺とその両端の角がそれぞれ等しい
1つずつ順番に解説していきます。
3辺がそれぞれ等しい
三角形の合同条件の1つ目は「3辺がそれぞれ等しい」です。
例えば、以下の図のように三角形ABCと三角形DEFがあったとき、
- AB=DE
- AC=DF
- BC=EF
が成り立っていれば(=3辺がそれぞれ等しければ)三角形ABCと三角形DEFは合同になります。
2辺とその間の角がそれぞれ等しい
三角形の合同条件の2つ目は「2辺とその間の角がそれぞれ等しい」です。
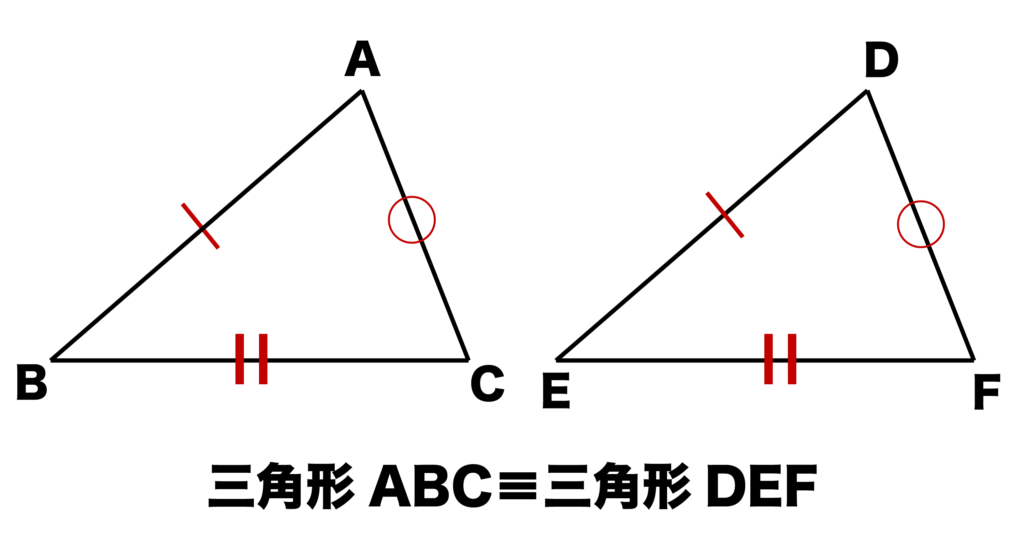
以下の図のように三角形ABCと三角形DEFがあったとき、
- AB=DE
- BC=EF
- ∠B=∠E
が成り立っていれば(=2辺とその間の角がそれぞれ等しければ)三角形ABCと三角形DEFは合同になります。
∠BはABとBCに挟まれており、∠EはDEとEFに挟まれていることがポイントです。
2辺と「その間の角」がそれぞれ等しくなければ合同とは言えません。
なので、例えば上記の図において
- AB=ED
- AC=DF
- ∠B=∠E
だった場合は三角形ABCと三角形DEFは合同であるとは言えません。
∠BはABとACに挟まれている角ではないですし、∠EもEDとDFに挟まれている角ではないからです。
三角形の合同条件=2辺と「その間の角」がそれぞれ等しいということをしっかりと頭に入れておきましょう。
1辺とその両端の角がそれぞれ等しい
最後の三角形の合同条件は「1辺とその両端の角がそれぞれ等しい」です。
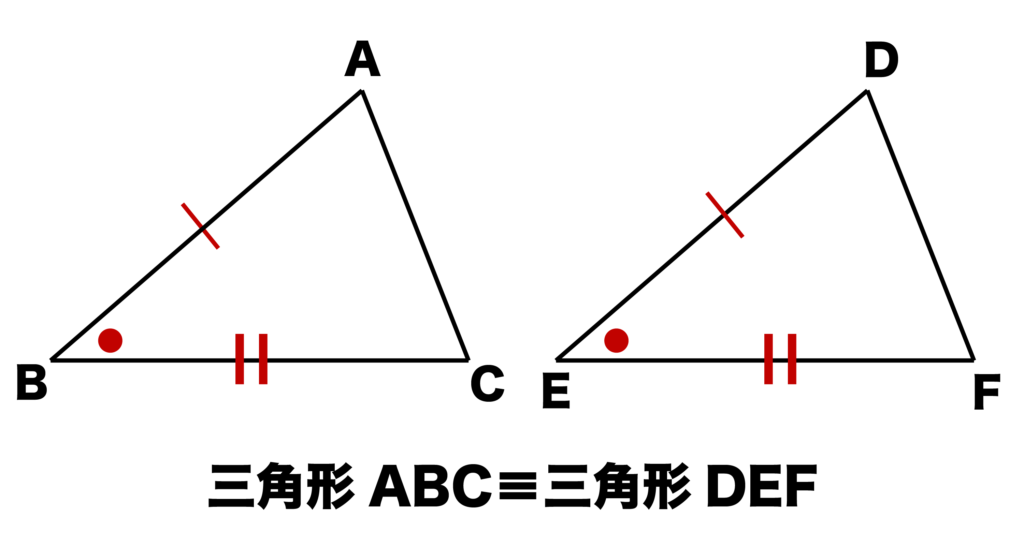
以下の図のように三角形ABCと三角形DEFがあったとき、
- BC=EF
- ∠B=∠E
- ∠C=∠F
が成り立っていれば(=1辺とその両端の角がそれぞれ等しければ)三角形ABCと三角形DEFは合同になります。
∠Bと∠CはBCの両端の角であり、∠Eと∠FはEFの両端の角であることがポイントです。
1辺と「その両端の角」がそれぞれ等しくなければ合同とは言えません。
なので、例えば上記の図において
- BC=EF・・・①
- ∠B=∠E・・・②
- ∠A=∠D・・・③
だった場合は、すぐに「①〜③より三角形ABCと三角形DEFは合同であると」は言うのは早計です。
三角形の内角の和は必ず180°なので、∠B=∠Eと∠A=∠Dより∠C=∠F・・・④が導けますね。
※三角形の内角の和は必ず180°であることの理由については内角・外角とは何かについて解説した記事をご覧ください。
④を導けたことによって、ようやく三角形の合同条件「1辺とその両端の角がそれぞれ等しい」を使うことが可能になるのでご注意ください。
直角三角形の合同条件
続いては直角三角形の合同条件について解説していきます。
直角三角形の合同条件は以下の2つです。
- 斜辺と他の1辺がそれぞれ等しい
- 斜辺と1つの鋭角がそれぞれ等しい
こちらも順番に詳しく解説していきます。
斜辺と他の1辺がそれぞれ等しい
直角三角形の合同条件の1つ目は「斜辺と他の1辺がそれぞれ等しい」です。
以下の図のように∠C=90°の直角三角形ABCと∠F=90°の直角三角形DEFがあったとき、
- 斜辺AB=斜辺DE
- BC=EF
が成り立っていれば(=斜辺と他の1辺がそれぞれ等しければ)直角三角形ABCと直角三角形DEFは合同になります。
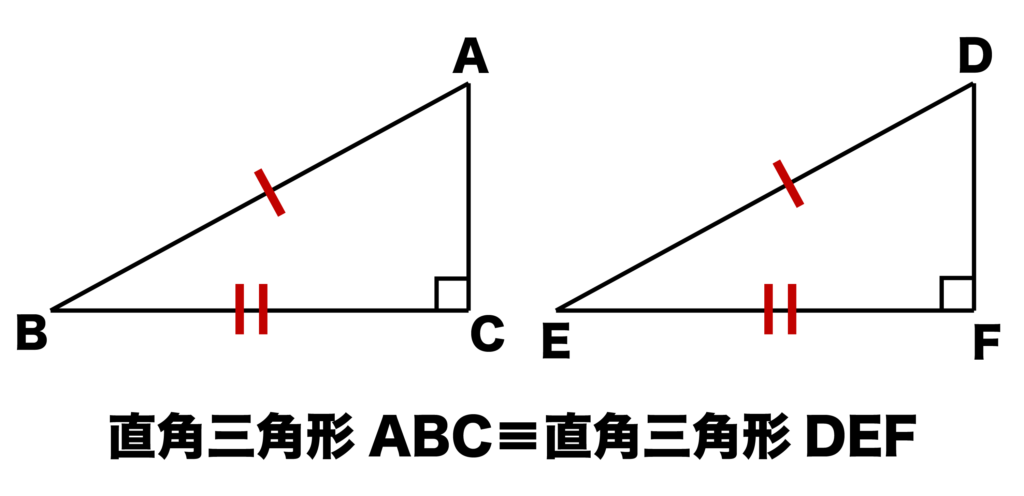
斜辺と「他の1辺」がそれぞれ等しければ合同になるので、BC=EFはAC=DFでも問題ありません。
斜辺と1つの鋭角がそれぞれ等しい
直角三角形の合同条件の2つ目は「斜辺と1つの鋭角がそれぞれ等しい」です。
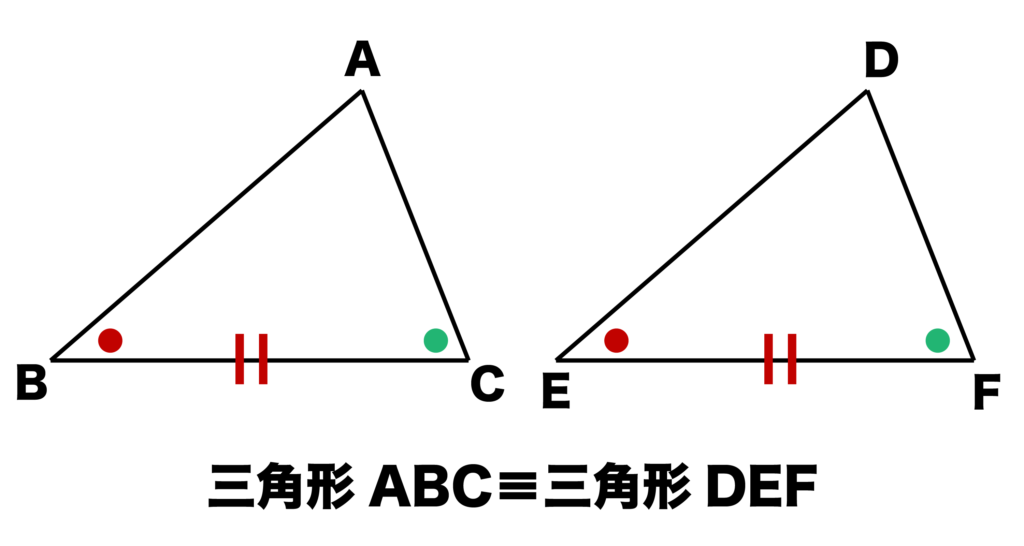
以下の図のように∠C=90°の直角三角形ABCと∠F=90°の直角三角形DEFがあったとき、
- 斜辺AB=斜辺DE
- ∠B=∠E
が成り立っていれば(=斜辺と1つの鋭角がそれぞれ等しければ)直角三角形ABCと直角三角形DEFは合同になります。
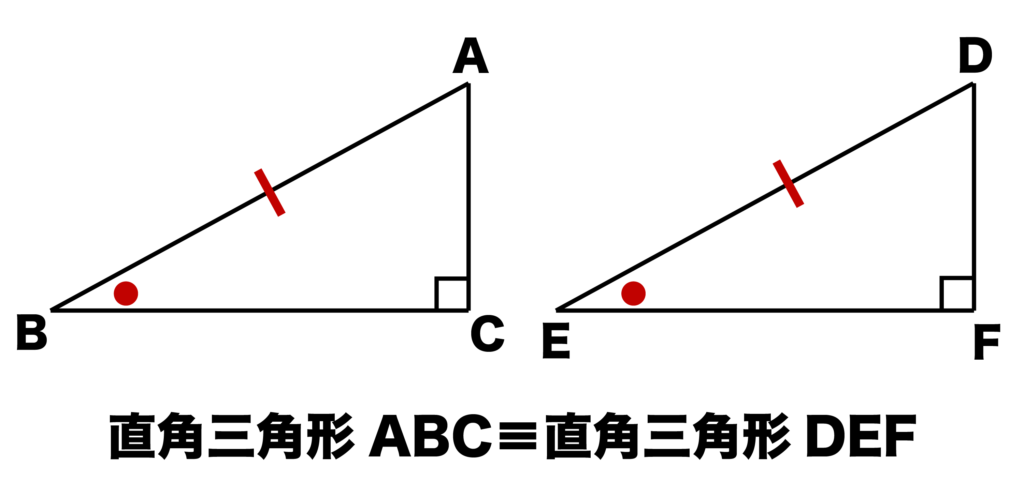
斜辺と「1つの鋭角」がそれぞれ等しければ合同になるので、∠B=∠Eは∠A=∠Dでも問題ありません。
三角形の合同条件はなぜ成り立つ?
では、三角形の合同条件や直角三角形の合同条件はなぜ成り立つのでしょうか?
結論から言いますと、三角形の合同条件・直角三角形の合同条件はなぜ成り立つかを追求すれば大学数学の内容に突入してしまいます。
なので、中学数学・高校数学では三角形の合同条件・直角三角形の合同条件は性質の1つとしてそのまま暗記してしまって問題ありません。
高校受験や大学入試・共通テストで三角形の合同条件・直角三角形の合同条件を証明せよという問題が出ることは絶対にありませんのでご安心ください。
三角形の合同条件・直角三角形の合同条件は証明問題で使うこともあるので、必ず暗記するようにしておきましょう。
三角形の合同条件に関する証明問題
最後に、三角形の合同条件に関する証明問題を1つご紹介しておきます。
とても基礎的な問題なので、必ず解けるようにしておきましょう。
【問題】
以下の図のようにAB=ACの二等辺三角形がある。∠ABE=∠ACDとなるように点Eと点Dをとったとき、AE=ADとなることを証明せよ。
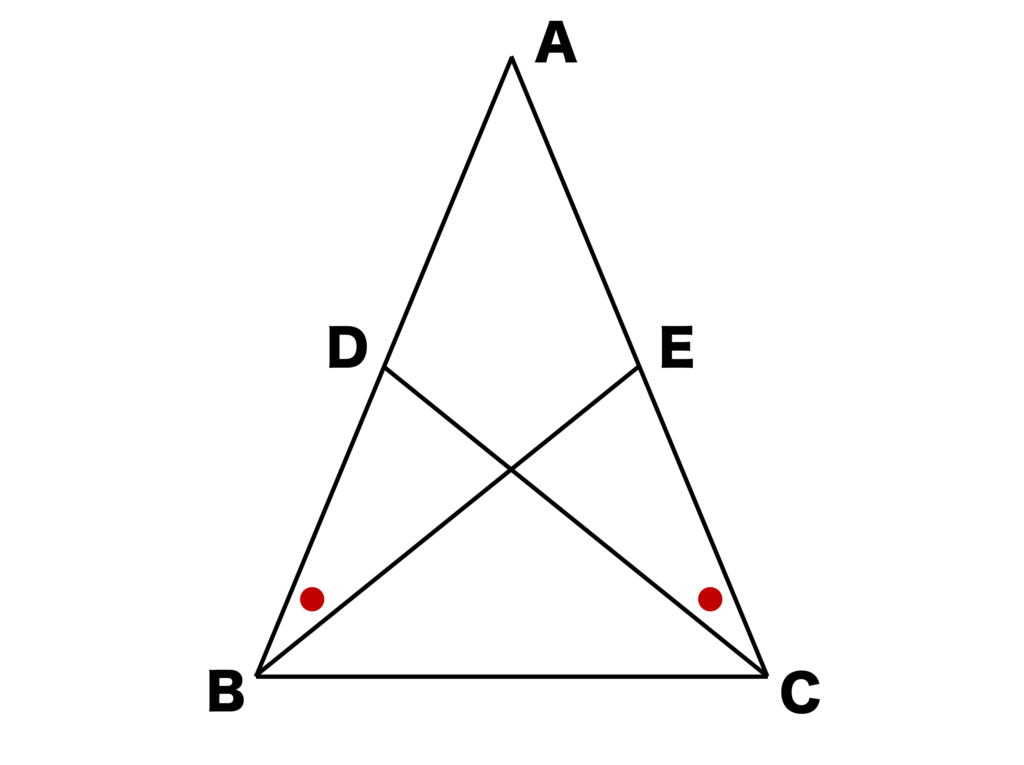
【解答&解説】
三角形ABEと三角形ACDにおいて、
- AB=AC・・・①
- ∠ABE=∠ACD・・・②
- ∠Aは共通・・・③
①・②・③より1辺とその両端の角がそれぞれ等しいので、三角形ABCと三角形ACDは合同となる。
よって、AE=ADが成り立つ。
【証明終】
※二等辺三角形の定義と定理(性質)について解説した記事もご用意しているので、ぜひ参考にしてください。
いかがでしたか?
今回は三角形と直角三角形の合同条件を図解で解説していきました。
繰り返しにはなりますが、三角形と直角三角形の合同条件は暗記必須です。呪文のように唱えて必ず覚えるようにしましょう。
※三角形の合同条件と一緒に三角形の相似条件も必ず覚えておきましょう。詳しくは三角形の相似条件について解説した記事をご覧ください。


