高校数学の数学Aにおける「図形の性質」では、中学数学で学習した二等辺三角形に関する知識の復習を取り上げている教科書もありますので、本記事でも二等辺三角形に関する知識を取り上げておきます。
今回は早稲田大学教育学部数学科を卒業した筆者が二等辺三角形とは何かについて解説した後、二等辺三角形に関する知識を一気に解説していきます。
本記事で中学数学・高校数学で必要な二等辺三角形に関する知識は網羅できますので、ぜひ最後までお読みください。
二等辺三角形とは?
まずは二等辺三角形とはどんな三角形かについて解説しておきます。
二等辺三角形は2つの辺の長さが等しい三角形のことです。辺の長さが等しい2つの辺を等辺、残りの1つの辺を底辺といいます。
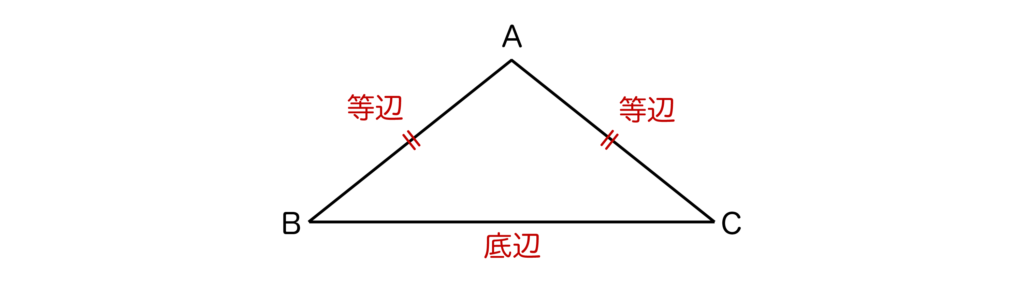
以上の図のように、AB=ACの二等辺三角形ABCにおいては∠B=∠Cが成り立ちます。
∠Bと∠Cは底角と呼ばれているので覚えておきましょう。また、∠A(=等しい2つの辺に挟まれた角)は頂角と呼ばれています。
以上が二等辺三角形の基本事項となります。二等辺三角形の定義について解説した記事もご用意しているので、ぜひ合わせてご覧ください。
二等辺三角形の重要な性質
先ほど解説した通り、二等辺三角形においては2つの底角の大きさは等しいです。これも重要な性質ですが、もう1つ重要な性質があるので覚えておきましょう。
以下の図のようにAB=ACの二等辺三角形ABCにおいて、点AからBCに対して下ろした垂線とBCとの交点をDとすると、ADはBCの垂直二等分線になります。
つまり、BD=DCとなります。また、このときADは頂角Aの二等分線にもなります。
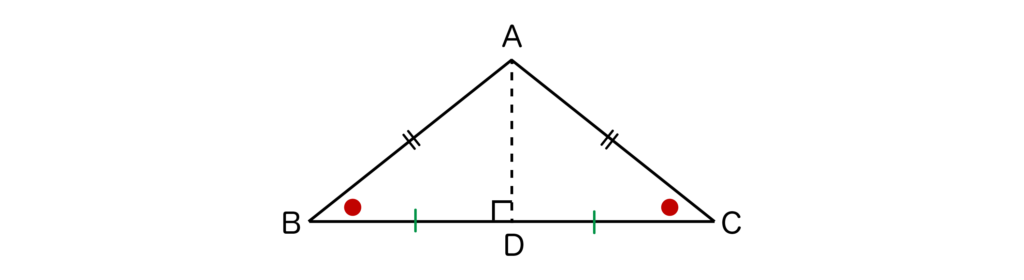
これは二等辺三角形に関する知識で一番重要といっても過言ではないので、必ず覚えておきましょう。
二等辺三角形の辺の長さの求め方
二等辺三角形の辺の長さの求め方は以下2つのパターンにわけることができます。
- 二等辺三角形の底辺の長さと高さがわかっている場合
- 頂角を挟む等しい2辺の長さと底辺の長さがわかっている場合
1の場合は、二等辺三角形の頂角を作っている点から底辺に対して垂線を下ろしたときにできる直角三角形に注目し、三平方の定理を利用することで頂角を挟む等しい2辺の長さを求めることが可能になります。
二等辺三角形と三平方の定理は非常に相性が良いので、必ず使えるようにしておきましょう。
二等辺三角形と三平方の定理の関係について解説した記事もご用意しているので、ぜひ合わせてご覧ください。
2の場合は1のときと同様に二等辺三角形の頂角を作っている点から底辺に対して垂線を下ろしたときにできる直角三角形に注目することで二等辺三角形の高さを求めることが可能になります。
二等辺三角形の辺の長さを求めるには三平方の定理が重要であるということを必ず理解しておきましょう。
1と2の詳細については二等辺三角形の辺の長さの求め方を図解でわかりやすく解説した記事を参考にしてください。
二等辺三角形の面積の求め方
三角形の面積は底辺×高さ÷2で求めることができるのでした。
二等辺三角形はもちろん三角形の一種なので、二等辺三角形の面積も底辺×高さ÷2で求めることができます。
二等辺三角形の辺の長さの求め方は先ほど解説した通りなので、その知識があれば二等辺三角形の面積も問題なく求めることが可能です。
二等辺三角形の面積の求め方について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
二等辺三角形の角度の求め方
続いては二等辺三角形の角度の求め方について解説します。
上記でも解説した通り、二等辺三角形の2つの底角は等しいという特徴があります。
なので、底角の大きさがわかっている場合は、頂角の大きさ=180°-(底角の大きさ×2)で求めることができます。
三角形の角は全部で3つあり、二等辺三角形の場合は底角が2つあるので「×2」となっています。
また、三角形の内角の和は180°でした。詳しくは内角・外角とは何かについて解説した記事をご覧ください。
逆に、頂角の大きさがわかっている場合は、底角の大きさ=(180°-頂角の大きさ)/2で求めることができます。
二等辺三角形辺の角度の求め方について詳しく解説した記事もご用意しているので、ぜひ合わせてご覧ください。
直角二等辺三角形について
二等辺三角形の一種として直角二等辺三角形があります。
直角二等辺三角形とは頂角が直角(=90°)である二等辺三角形のことです。
直角二等辺三角形の底角の大きさは(180°-90°)/2=45°になります。
また、直角二等辺三角形の辺の比は以下の図のように必ず1:1:√2になるという特徴があります。これは必ず覚えておきましょう。
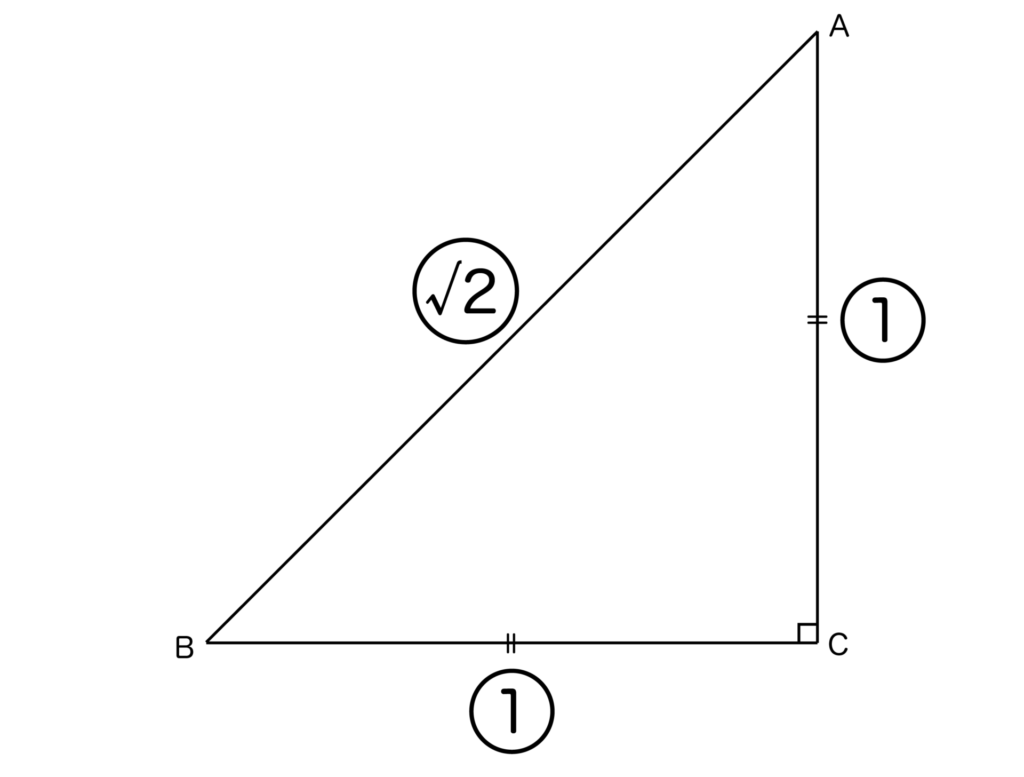
この比を利用することで、直角三角形の辺の長さを一瞬で求めることができるようになります。
例えば、上記の直角三角形ABCにおいてAC=BC=8cmのとき、ABの長さ=8×√2=8√2[cm]となります。
直角二等辺三角形の辺の長さについて詳しく解説した記事もご用意しているので、ぜひ合わせてご覧ください。
特殊な形の二等辺三角形
頂角が120°と15°の二等辺三角形は特殊な形の二等辺三角形として覚えておくと便利な事柄がいくつかあるのでご紹介しておきます。
頂角=120°の二等辺三角形
以下の図のように頂角である∠A=120°の二等辺三角形ABCにおいては、AB:AC:BC=1:1:√3となります。

また、以下の図のように点Aから底辺BCに対して垂線ADをおろしたとき、∠BAD=∠CAD=60°となるので、三角形ABDと三角形ACDはともに60°型の直角三角形となります。
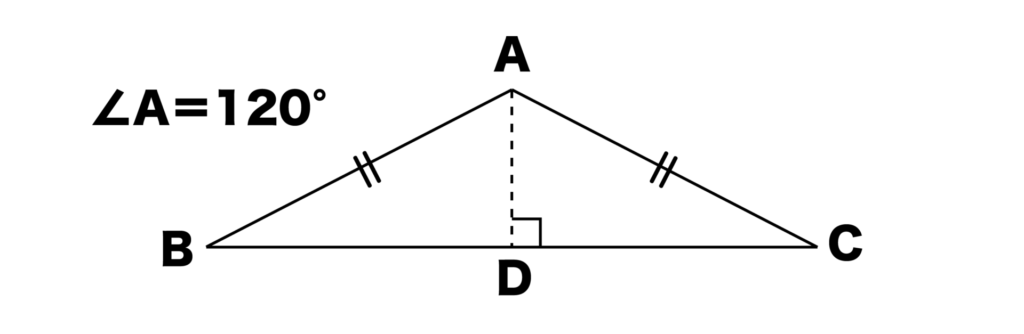
つまり、AD:AB:BD=AD:AC:CD=1:2:√3となります。
以上の2つは非常に重要なので必ず頭に入れておきましょう。
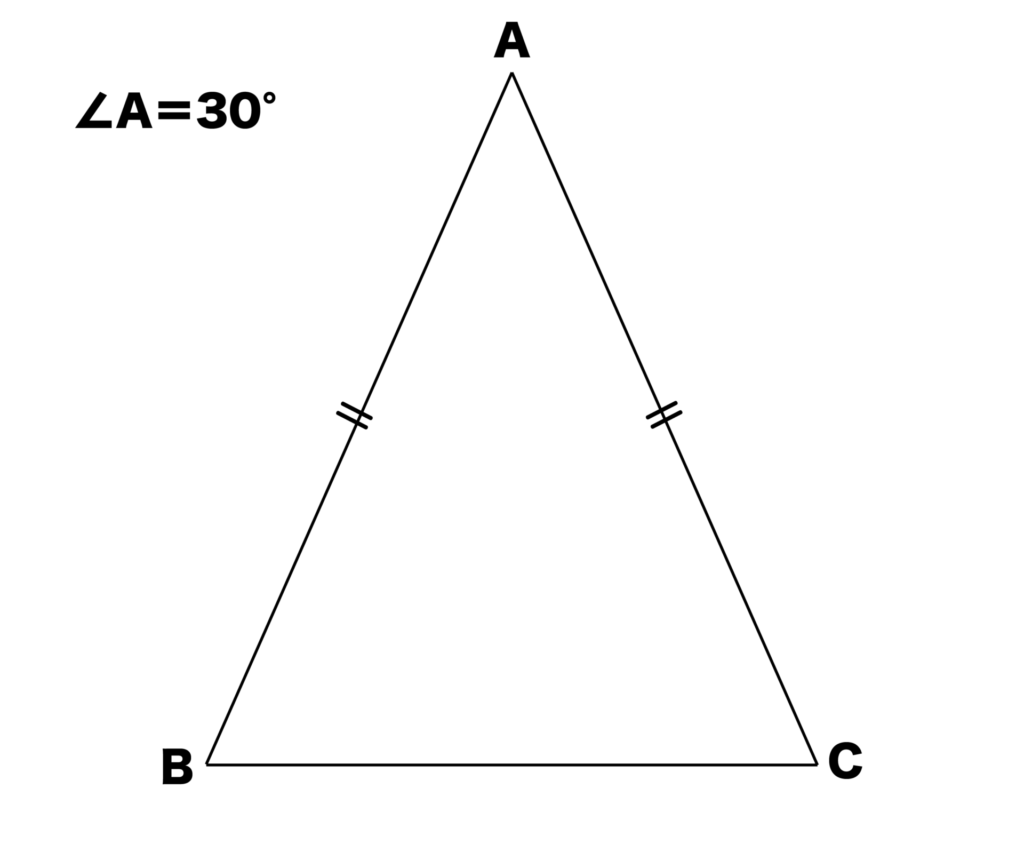
頂角=30°の二等辺三角形
以下の図のように頂角である∠A=30°の二等辺三角形ABCにおいては、AB:AC:BC=(√2+√6):(√2+√6):2となります。
これはかなり応用的な内容ですので、余裕があれば覚えておく程度で問題ありません。
ちなみに、先ほどと同様に点Aから底辺BCに対して垂線ADをおろすと、∠BAD=∠CAD=15°となりますね。
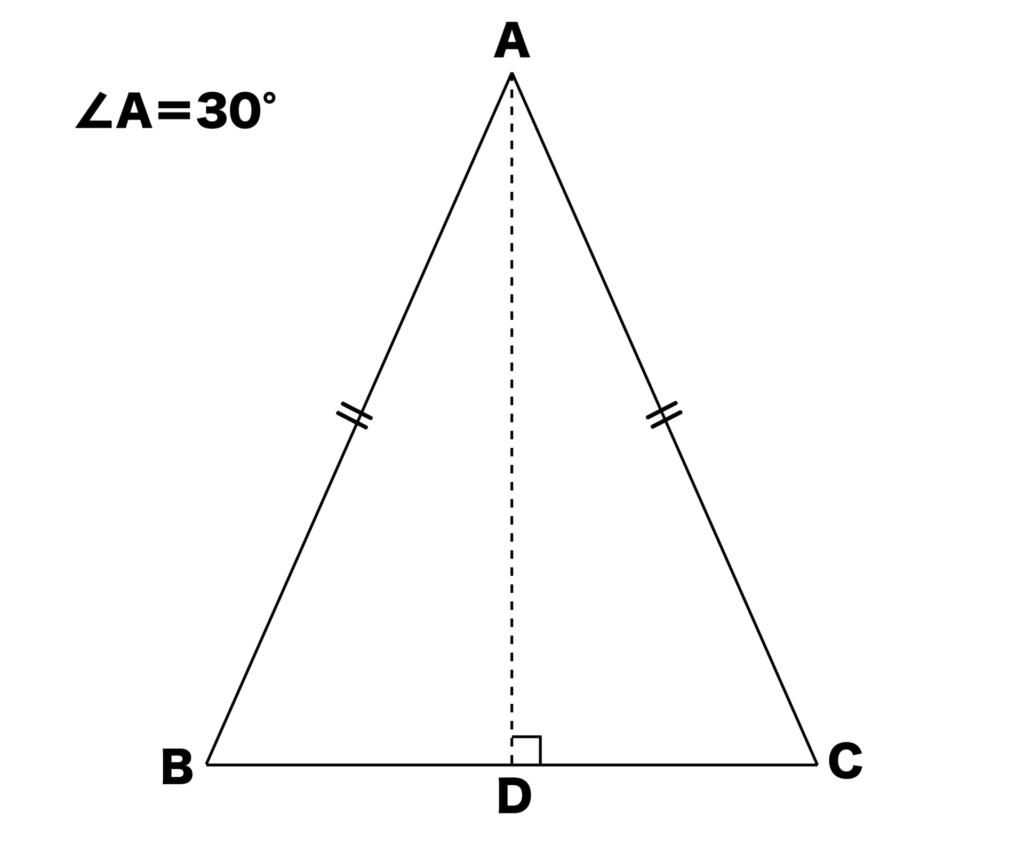
15°型の直角三角形の比はBD:AD:AB=CD:AD:AC=1:(2+√3):(√2+√6)となります。
これも応用的な内容なので、余裕があれば覚えておきましょう。
詳しくは二等辺三角形と比の関係について解説した記事をご覧ください。
いかがでしたでしょうか?
今回は二等辺三角形とはについて解説した後、二等辺三角形に関する知識を一気にご紹介していきました。
二等辺三角形に関して復習したいことがあればまた本記事を見返していただければと思います。


