二等辺三角形では1:2:√3のように必ず覚えておくべき比はありませんが、知っていると便利な比はあります。
※二等辺三角形の一種である直角三角形の比は暗記必須です。本記事でもご紹介していきます。
というわけで今回は早稲田大学教育学部数学科を卒業した筆者が二等辺三角形と比の関係について図解で解説していきます。
数学や図形が苦手な生徒でも理解できるよう、わかりやすく解説していくのでぜひ最後までご覧ください。
二等辺三角形の比(頂角=120°の場合)
まずご紹介するのは頂角=120°の二等辺三角形の比です。頂角とは2つの等しい長さの変に挟まれた角のことです。
以下の図のように頂角である∠A=120°の二等辺三角形ABCの辺の比を求めてみましょう。

まずは点Aから底辺BCに垂線をおろし、BCとの交点をDとします。
※二等辺三角形の底辺の長さの求め方について解説した記事もぜひ合わせてご覧ください。
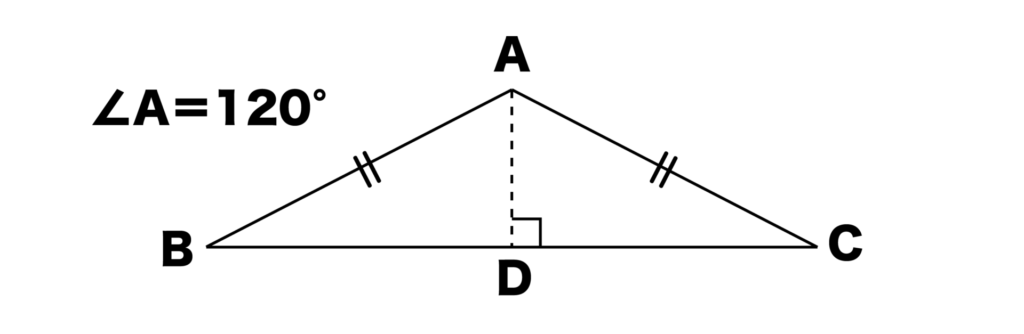
このとき、ADは∠Aの二等分線かつBCの垂直二等分線になるのでした。
※詳しくは二等辺三角形の定義と定理(性質)について解説した記事をご覧ください。
よって、∠BAD=120°÷2=60°になります。また、∠BDA=90°なので、三角形ABDは60°型の直角三角形となります。
よってAD:AB:BD=1:2:√3になります。
ここで、ABの辺の長さを2aとおいてみましょう。すると、AD=aとなるので、BD=√3aになりますね。
BC=2×BD=2√3aとなります。
したがって、頂角=120°の二等辺三角形の比AB:AC:BC=2a:2a:2√3a=1:1:√3となります。
これは覚えておくと非常に便利なので、余力がある人はぜひ覚えておきましょう。
※二等辺三角形の辺の長さの求め方を図解でわかりやすく解説した記事もご用意しているので、ぜひ参考にしてください。
二等辺三角形の比(頂角=30°の場合)
次は頂角=30°の二等辺三角形の比です。以下の図のように頂角である∠A=30°の二等辺三角形ABCの辺の比を求めてみましょう。
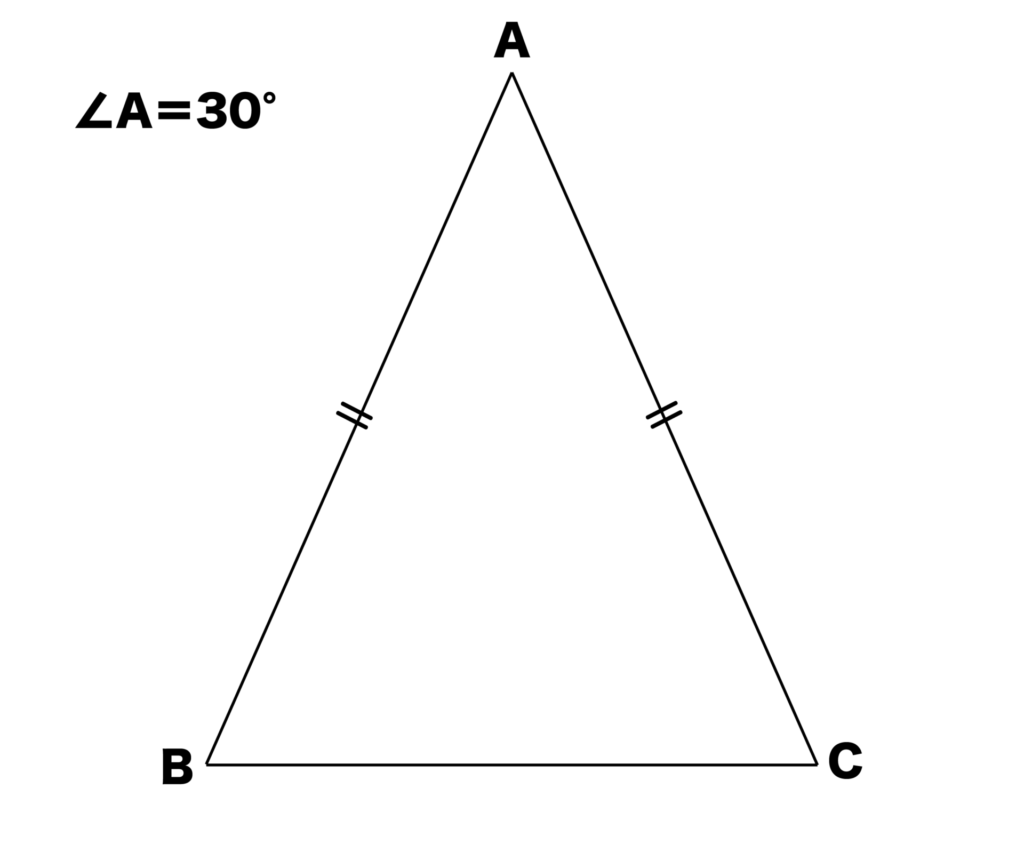
先ほどと同様に、まずは点AからBCに対して垂線ADをおろします。
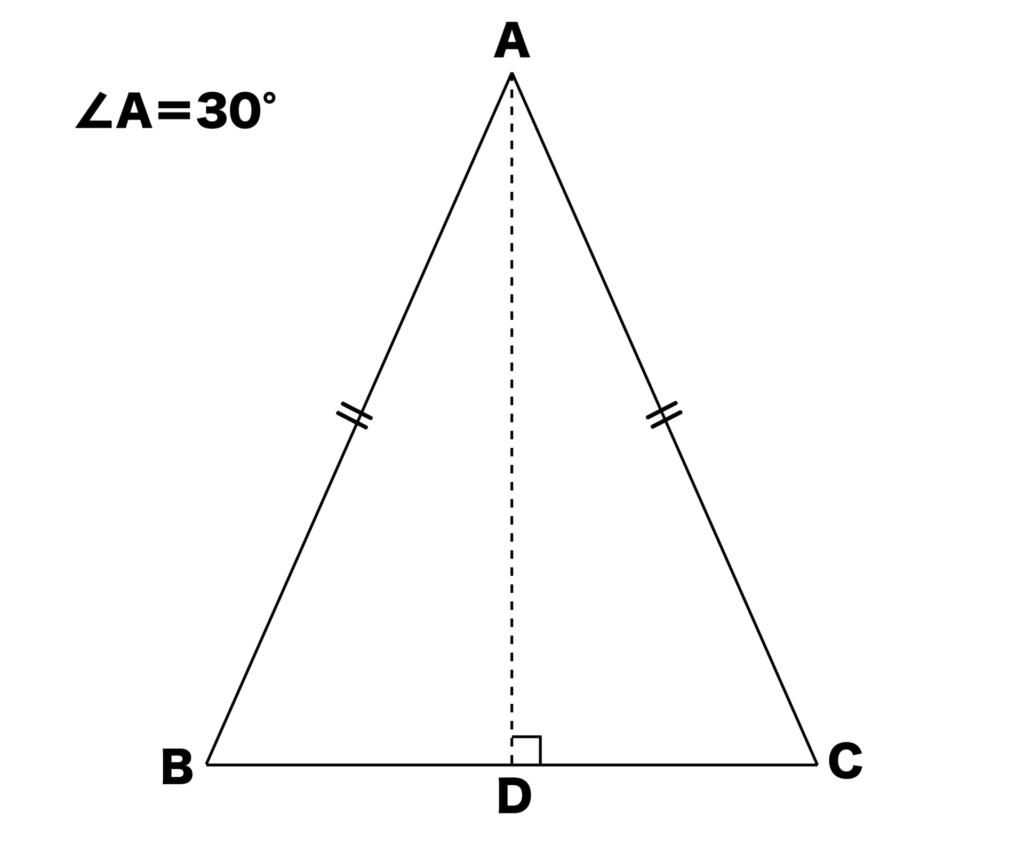
すると、∠BAD=15°となりますね。∠BDA=90°なので、∠ABD=180°-(15°+90°)=75°となります。
※三角形の内角の和=180°でした。詳しくは内角・外角とは何かについて解説した記事をご覧ください。
つまり、三角形ABDは15°型の直角三角形となります。
15°型の直角三角形の比はBD:AD:AB=1:(2+√3):(√2+√6)となります。
※15°型の直角三角形の比は教科書では登場しない応用的な内容ですが、偏差値の高い学校を受験予定の人は必ず覚えておきましょう。
ここで、BD=aとおきます。すると、AB=(√2+√6)aですね。また、BC=2aです。
したがって、頂角=30°の二等辺三角形の比AB:AC:BC=(√2+√6)a:(√2+√6)a:2a=(√2+√6):(√2+√6):2となります。
少し応用的な内容ですので、無理に覚える必要はありません。
二等辺三角形の比(頂角=60°の場合)
次は頂角=60°の二等辺三角形を見てみましょう。
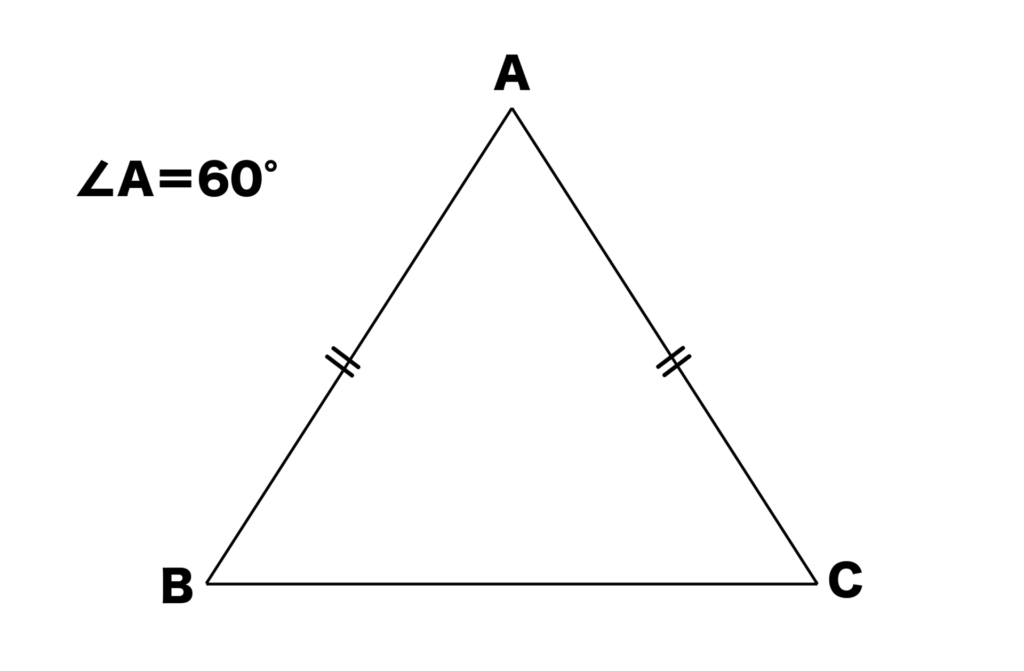
二等辺三角形の底角は等しいので、∠A=60°であることから、∠Bも∠Cも60°であることがわかります。
つまり、頂角=60°の二等辺三角形は正三角形となります。
正三角形は3つの辺の長さがすべて等しいので、AB:AC:BC=1:1:1となります。
直角二等辺三角形の比
最後は直角二等辺三角形の比についてです。
直角二等辺三角形とは、頂角が90°である三角形のことです。そして、直角二等辺三角形の辺の比は以下の図のように、必ず1:1:√2になります。
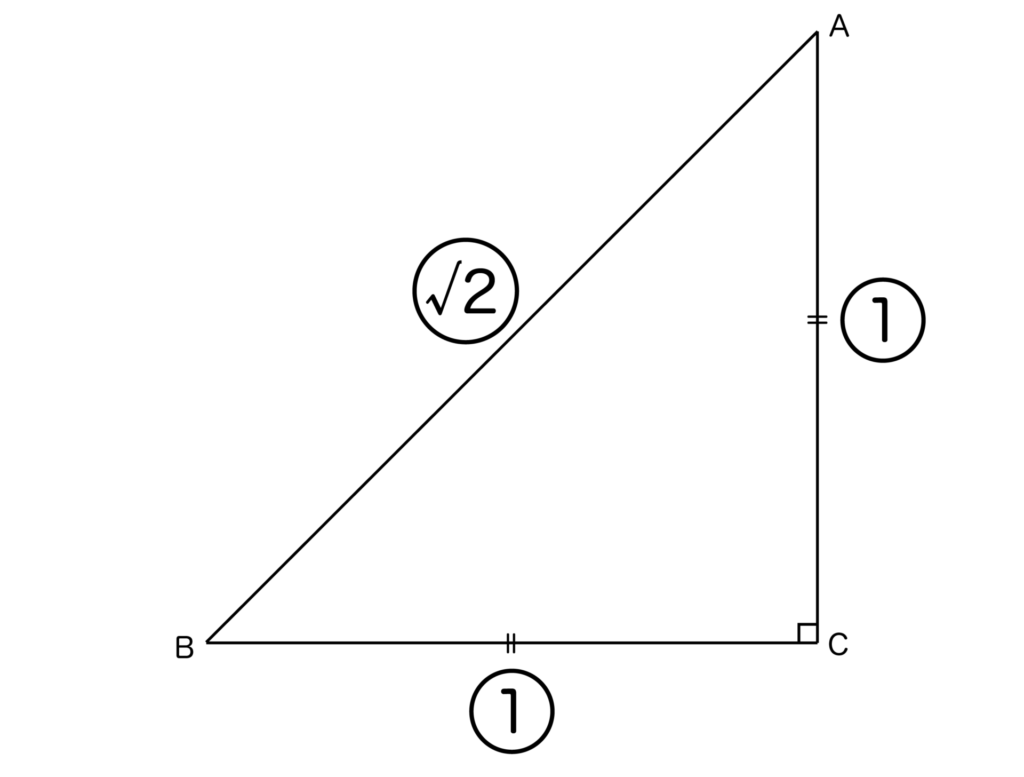
辺の比が1:1:√2になる理由ですが、AC=BC=aとすると、三平方の定理より
AB2=a2+a2=2a2
が成り立ちます。よって、AB>0よりAB=a√2となるので、AC:BC:AB=a:a:a√2=1:1:√2となります。
※二等辺三角形と三平方の定理の関係について解説した記事もぜひ合わせてご覧ください。
直角二等辺三角形の比は入試問題を解く上での基礎知識となりますので、必ず暗記しておきましょう。
直角二等辺三角形の辺の長さを10秒で求める方法をご紹介した記事もご用意しているので、そちらもぜひ参考にしてください。
いかがでしたか?
今回は二等辺三角形と比の関係について解説していきました。
頂角=120°に二等辺三角形の比はそこまで使用頻度は高くありませんが、覚えておくと便利ではあります。1:1:√3と非常にシンプルなので、ぜひこれを機に覚えておきましょう。