二等辺三角形の面積の求め方！裏ワザはある？図解で徹底解説

二等辺三角形の面積の求め方は二等辺三角形の辺の長さの求め方をしっかりと理解していれば全然難しくないのでご安心ください。

二等辺三角形の面積を求める問題が直接入試で出題されることは稀ですが、図形問題の基本となるので、必ずできるようにしておきましょう。

今回は早稲田大学教育学部数学科を卒業した筆者が二等辺三角形の面積の求め方について図解でわかりやすく解説していきます。

また、二等辺三角形の面積の求め方の裏ワザもご紹介していくので、ぜひ最後までお読みください。

二等辺三角形の面積の求め方

三角形の面積は底辺×高さ÷2で求めることができるのでした。

したがって、二等辺三角形のおいても底辺と高さがわかれば面積を求めることができます。

というわけで、ここからは底辺がわからない場合と高さがわからない場合のそれぞれの面積の求め方について解説します。

底辺がわからない場合

例えば、以下の図のようにAB＝30、AD＝15の二等辺三角形ABCの面積を求めてみましょう。

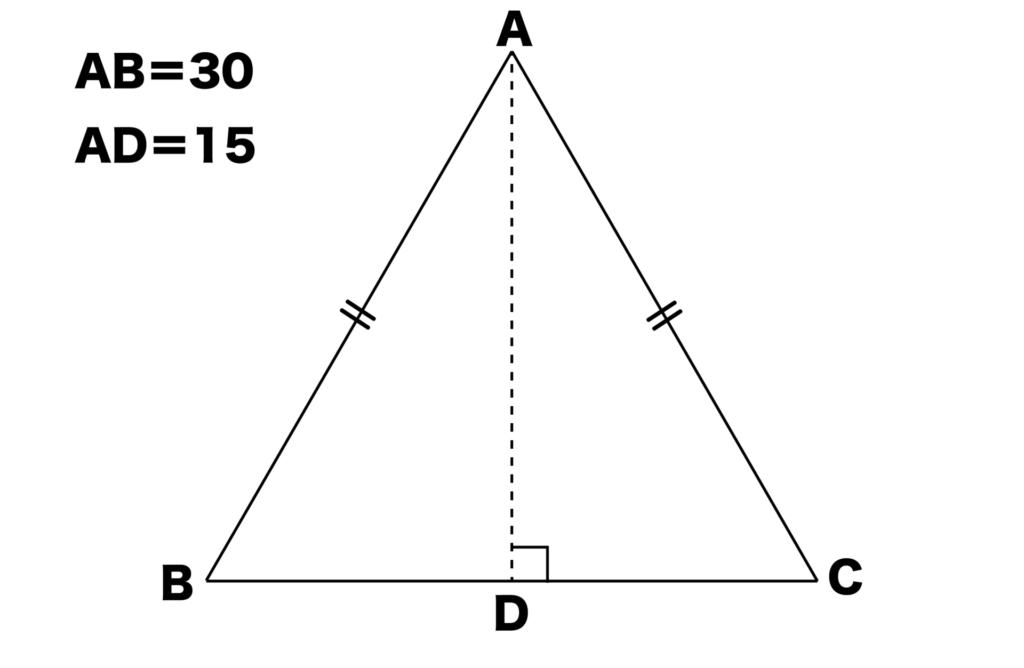
三角形ABDに注目すると、∠ADB＝90°なので三角形ABDは直角三角形です。よって、三平方の定理が使えます。

AB²＝AD²＋BD²より、30²＝15²＋BD²となるので、

900＝225＋BD²よりBD²＝675となります。

BD>0より、BD＝√675＝15√3となります。

※BD＝√675＝15√3となる理由がわからない人は平方根とは何かについて解説した記事をご覧ください。

ここで、ADはBCの垂直二等分線となるので、BC＝2×BDとなります。

※ADがBCの垂直二等分線となる理由がわからない人は二等辺三角形の定義と定理（性質）について解説した記事をご覧ください。

つまり、BC＝2×15√3＝30√3となります。

これで二等辺三角形ABCの底辺（BC）が求まりました。

※二等辺三角形の底辺の長さの求め方について詳しく解説した記事もぜひ合わせてご覧ください。

よって、二等辺三角形ABCの面積＝BC×AD÷2＝30√3×15÷2＝225√3となります。

二等辺三角形と三平方の定理は非常に相性が良いので、必ず使えるようにしておきましょう。

二等辺三角形と三平方の定理の関係について解説した記事もご用意しているので、ぜひ合わせてご覧ください。

高さがわからない場合

続いては二等辺三角形の高さがわからない場合の面積の求め方です。

例えば、以下の図のようにBC（底辺）＝16、AB＝AC＝20の二等辺三角形ABCの面積を求めてみます。

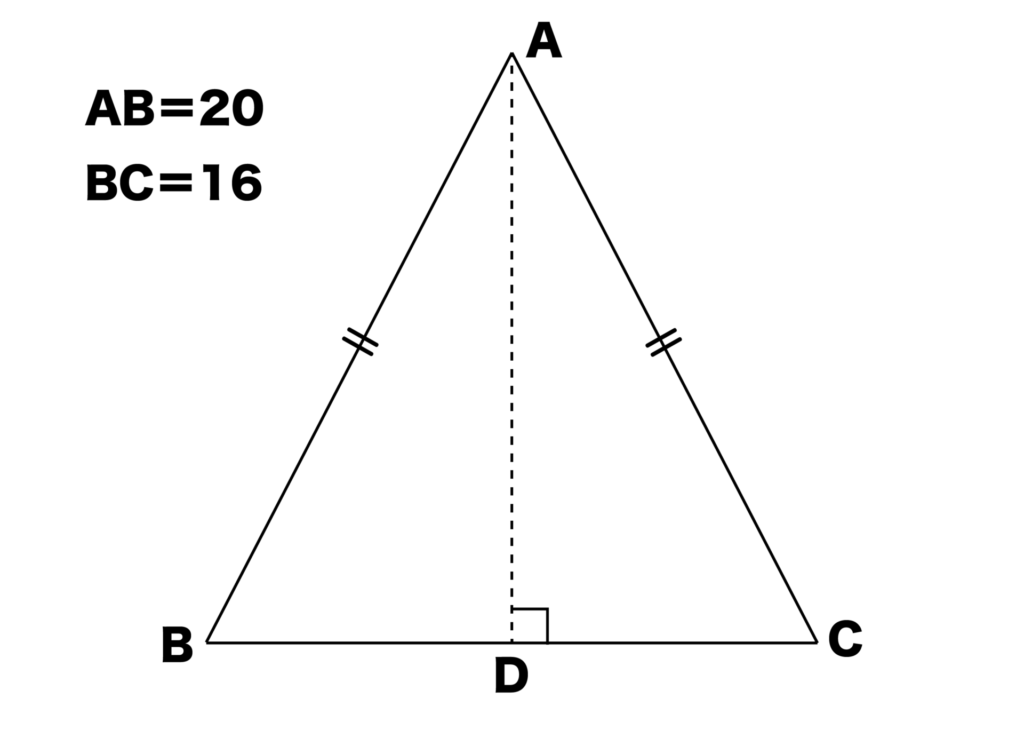
先ほどと同様に、三角形ABDは直角三角形なので、AB²＝AD²＋BD²が成り立ちます。

BD＝BC/2＝16/2＝8なので、20²＝AD²＋8²より、336＝AD²となります。

AD>0より、AD＝4√21となります。

これで二等辺三角形のABCの底辺と高さが求まったので、面積が求められます。

※二等辺三角形の高さの求め方について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。

二等辺三角形のABCの面積＝16×4√21÷2＝32√21となります。

二等辺三角形の面積を求めるには底辺や高さを求めることを意識しましょう。

二等辺三角形の辺の長さの求め方について詳しく解説した記事もぜひ合わせてご覧ください。

二等辺三角形の面積の求め方に裏ワザはある？

頂角が120°の二等辺三角形の面積を求めるには裏ワザのようなテクニックを知っておく必要があります。

以下の図のような∠A＝120°、AB＝AC＝10の二等辺三角形ABCの面積を求めてみましょう。

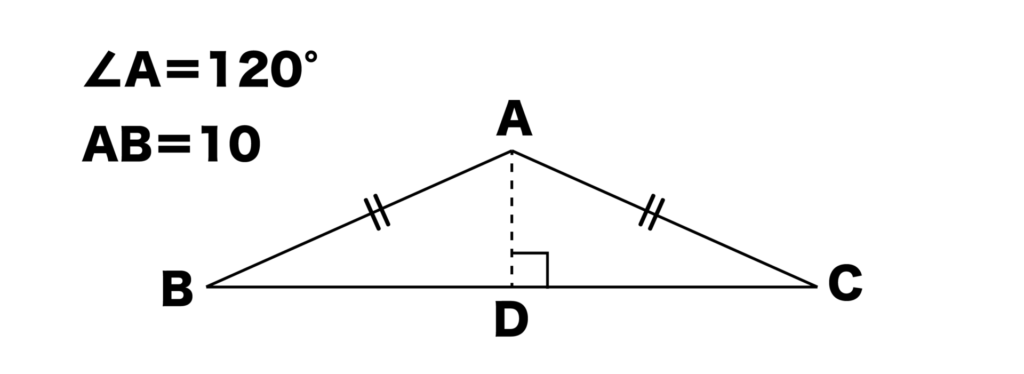
二等辺三角形の性質より、ADは∠Aの二等分線になります。

したがって、∠BAD＝120°÷2＝60°となります。また、∠BDA＝90°です。

※二等辺三角形辺の角度の求め方について解説した記事もぜひ合わせてご覧ください。

よって、三角形ABDは60°型の直角三角形であることがわかります。

よって、AD：AB：BD＝1：2：√3になります。

AB＝10より、AD＝5となります。また、BD＝5×√3＝5√3です。

したがって、BC＝2×5√3＝10√3です。

これで底辺（BC）と高さ（AD）が求まりました。

よって、二等辺三角形ABCの面積＝10√3×5÷2＝25√3となります。

頂角が120°の二等辺三角形においてはどれか1つの辺の長さがわかっていれば面積を求めることができます。

直角二等辺三角形の面積の求め方

二等辺三角形の一種に直角二等辺三角形がありますが、直角二等辺三角形の面積は直角を挟む2辺をかけて2で割ることで求められます。

例えば以下の図のようにAB＝20の直角二等辺三角形ABCの面積を求めてみましょう。

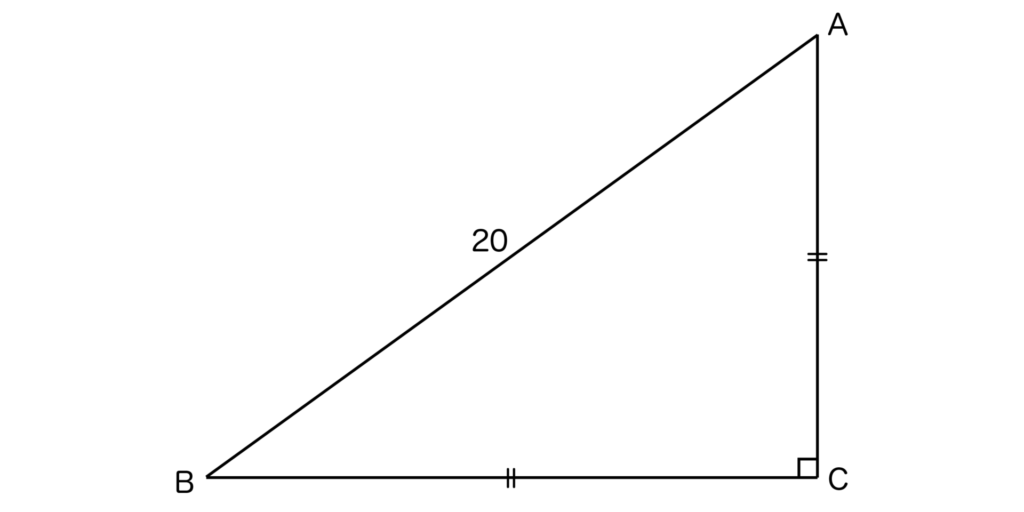
直角二等辺三角形の辺の比はAC：BC：AB＝1：1：√2でしたね。

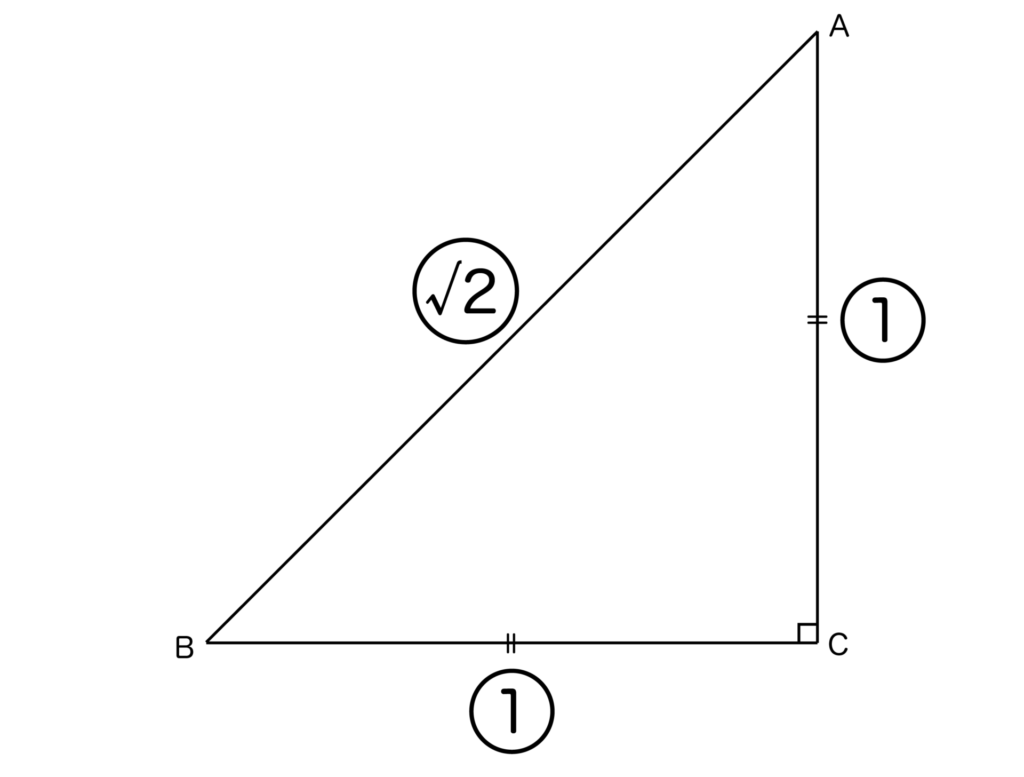
よって、AC＝BC＝20/√2＝10√2です。

したがって、直角二等辺三角形ABCの面積＝10√2×10√2÷2＝100となります。

直角二等辺三角形の面積を求める場合も、二等辺三角形のときと同じように底辺と高さ（＝直角を挟む2辺の長さ）を求める必要があります。

直角二等辺三角形の辺の長さを10秒で求める方法をご紹介した記事もご用意しているので、ぜひ参考にしてください。

いかがでしたか？今回は二等辺三角形の面積の求め方について解説しました。

二等辺三角形の面積を求めるには二等辺三角形の辺の長さを求める力が必要ということをしっかり理解しておきましょう。