二等辺三角形と三平方の定理は密接に関係しており、三平方の定理を使うことで二等辺三角形の辺の長さや高さを求めたりすることができます。
数学の図形問題を攻略するためには、二等辺三角形と三平方の定理の関係性はしっかりと理解しておく必要があります。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が二等辺三角形と三平方の定理の関係について図解でわかりやすく解説していきます。
数学や図形問題が苦手な人でも理解できるように解説していくので、ぜひ参考にしてください。
二等辺三角形と三平方の定理のおさらい
まずは二等辺三角形と三平方の定理に簡単におさらいしておきましょう。
すでに理解できている人は飛ばしていただいて問題ありません。
まず、二等辺三角形とはその名の通り2つの辺の長さが等しい三角形のことです。
※二等辺三角形の定義と定理(性質)について解説した記事もぜひ合わせてご覧ください。
例えば、以下の三角形ABCはAB=ACなので二等辺三角形となります。
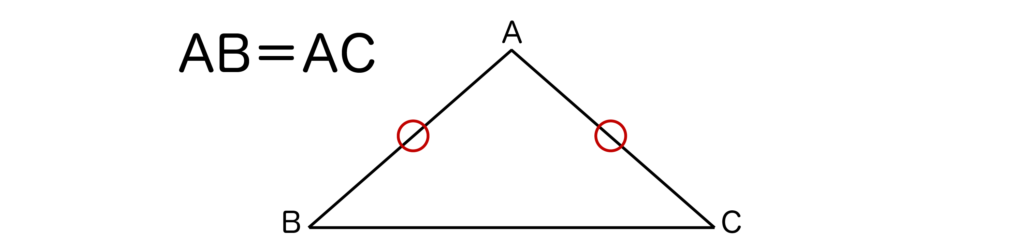
二等辺三角形においては、上記の図の場合∠B=∠Cとなります。
※二等辺三角形辺の角度の求め方について解説した記事もぜひ合わせてご覧ください。
また、二等辺三角形の頂角の二等分線は底辺を垂直に二等分します。
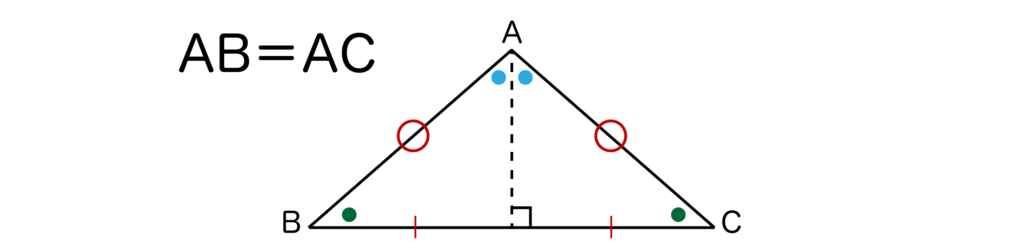
以上でご紹介した二等辺三角形の性質は必ず覚えておきましょう。
次は三平方の定理です。三平方の定理はピタゴラスの定理とも呼ばれており、直角三角形ABCにおいて、AB2=AC2+BC2が成り立つことです(以下の図参照)
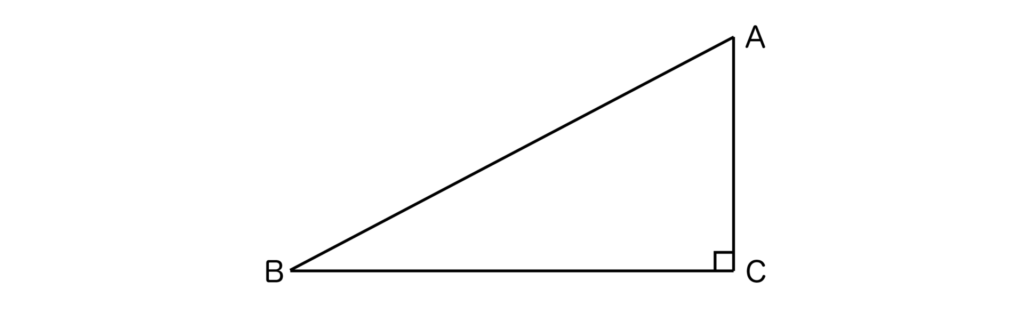
つまり、斜辺の2乗の大きさはその他の2辺の2乗の和に等しいというのが三平方の定理です。
二等辺三角形と三平方の定理の関係その1
二等辺三角形と三平方の定理を復習したところで、ここからは二等辺三角形と三平方の定理の関係について解説していきます。
1つ目ですが、二等辺三角形が直角二等辺三角形である場合、三平方の定理を使って辺の長さを求めることができます。
例えば、以下の図ようにAC=15の直角二等辺三角形ABCがあるとします。このとき、ABの長さを求めてみましょう。
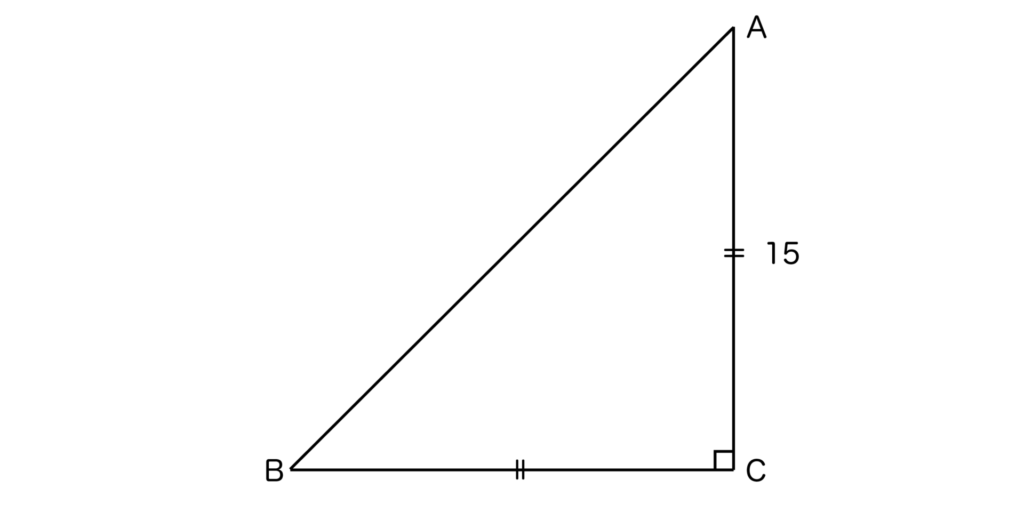
直角二等辺三角形も二等辺三角形の一種なので、AC=BC=15となります。
∠C=90°なので、三平方の定理を使うことができます。
三平方の定理より、AB2=AC2+BC2=152+152=225+225=450です。
AB>0なので、AB=15√2となります。
※直角二等辺三角形の辺の比は1:1:√2なので(斜辺=√2)AB=BC×√2=15√2と求めることも可能です。
直角二等辺三角形では、1つの辺の長さがわかれば自動的に残り2つの辺の長さも三平方の定理を活用して求めることが可能です。
※直角二等辺三角形の辺の長さを10秒で求める方法について解説した記事もぜひ合わせてご覧ください。
二等辺三角形と三平方の定理の関係その2
二等辺三角形と三平方の定理の関係2つ目ですが、二等辺三角形の頂角の二等分線は底辺を垂直に二等分するという性質を使って二等辺三角形の高さを求めることができます。
例えば、例えば、以下の図ようにAB=AC=10、BC=16の二等辺三角形ABCがあるとします。
このとき、ADの長さを求めてみましょう。
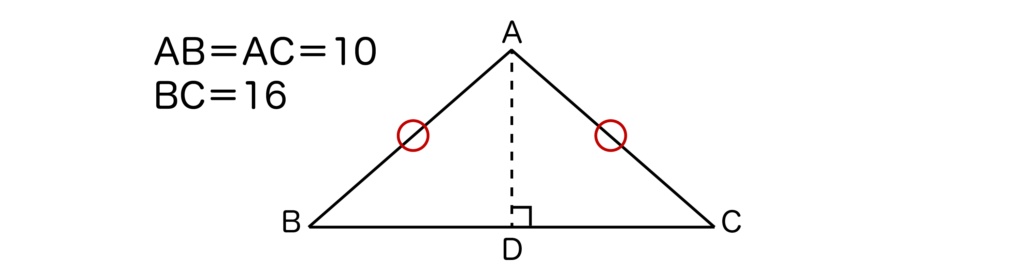
二等辺三角形の頂角の二等分線は底辺を垂直に二等分するので、BD=BC/2=16/2=8となります。
※二等辺三角形の底辺の長さの求め方について詳しく解説した記事もぜひ合わせてご覧ください。
ここで、三角形ABDに注目すると、三角形ABDは直角三角形なので、三平方の定理より
AB2=AD2+BD2が成り立ちます。AB=10、BD=8を代入して、
102=AD2+82より、AD2=36となります。AD>0より、AD=6となります。
つまり、二等辺三角形ABCの高さは6であるというです。
※二等辺三角形の高さの求め方について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
以上のように「二等辺三角形の頂角から垂線を下ろして三平方の定理を使う」というテクニックはよく使用するので必ず頭に入れておきましょう。
いかがでしたか?
今回は二等辺三角形と三平方の定理の関係について解説していきました。
本記事でご紹介したことは全て基本的な事柄ですので、必ず理解しておきましょう。