今回は高校数学の数学1における「データの分析」で登場する散布図を取り上げます。
散布図は相関図とも呼ばれており、2つの変量(後ほど解説します)の間に成り立つ関係を知るのに役立ちます。
本記事では早稲田大学教育学部数学科を卒業した筆者が散布図とは何かだけでなく、散布図の書き方や見方、相関関係との関係についても図表を使いながらわかりやすく解説していきます。
数学やデータの分析が苦手な人でも理解できるように解説していくので、ぜひ最後までご覧ください。
散布図とは?
散布図とは何かについて解説する前に、まずは散布図を何のために使うかのか?について解説していきます。
散布図は冒頭でも述べた通り相関図とも呼ばれています。散布図を使うことで、例えば
- 「数学な得意」な人は「物理も得意」か?
- 「サッカーが得意」な人は「短距離走が速い」か?
などを調べることができます。
「数学な得意かどうか」や「短距離走が速いかどうか」など1つの基準で集めたデータのことを1変量データといい、散布図では1変量データ同士の関係を知ることができます。
つまり、散布図では2変量データの分析を行うというわけです。
2変量データの分析では、一方の量が変化したとき、それに伴ってもう一方の量がどのように変化するか?を調べます。
例えば、一人ひとりについての数学の点数と物理の点数を以下のように座標平面で表すことを考えてみます。
以下の図は数学=50点、物理=40点の生徒のデータを示しています。
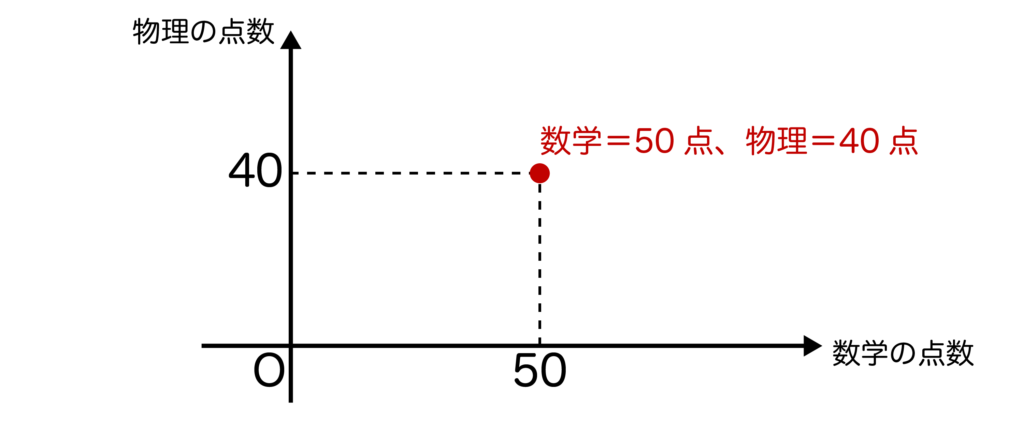
以上のように、採集したデータすべてを座標平面上に示したグラフのことを散布図もしくは相関図といいます。
散布図を活用することで2変量データの関係が可視化され、わかりやすくなります。
散布図の書き方・見方(正の相関と負の相関)
ここからは例題をもとに散布図を実際に書いて分析していきましょう。
【例題】
A君・B君・C君・D君の4人が数学と物理のテスト(ともに100点満点)を受験した。この4人の点数は以下の通りである。以下のデータをもとにして散布図を書きなさい。
| A君 | B君 | C君 | D君 | |
|---|---|---|---|---|
| 数学[点] | 15 | 30 | 60 | 70 |
| 物理[点] | 14 | 32 | 55 | 68 |
【解答&解説】
散布図の書き方は以下の2ステップで非常に簡単です。
- 横軸と縦軸に必要なデータを取る
- 採集したデータを点として図示する
順番に解説していきます。
横軸と縦軸に必要なデータを取る
まずは座標平面上の横軸と縦軸に必要なデータを取りましょう。
今回は数学の点数と物理の点数の散布図を書きたいので、横軸に数学の点数、縦軸に物理の点数を取ってみましょう。
※横軸に物理の点数、縦軸に数学の点数を取っても別に問題ありません。

原点Oも忘れずに書いてください。
採集したデータを点として図示する
横軸と縦軸が決まったら、次は採集したデータを点として図示していきます。
今回はA君〜D君の合計4つのデータがあります。そのすべてを座標平面上に図示していくと、以下のようになりますね。
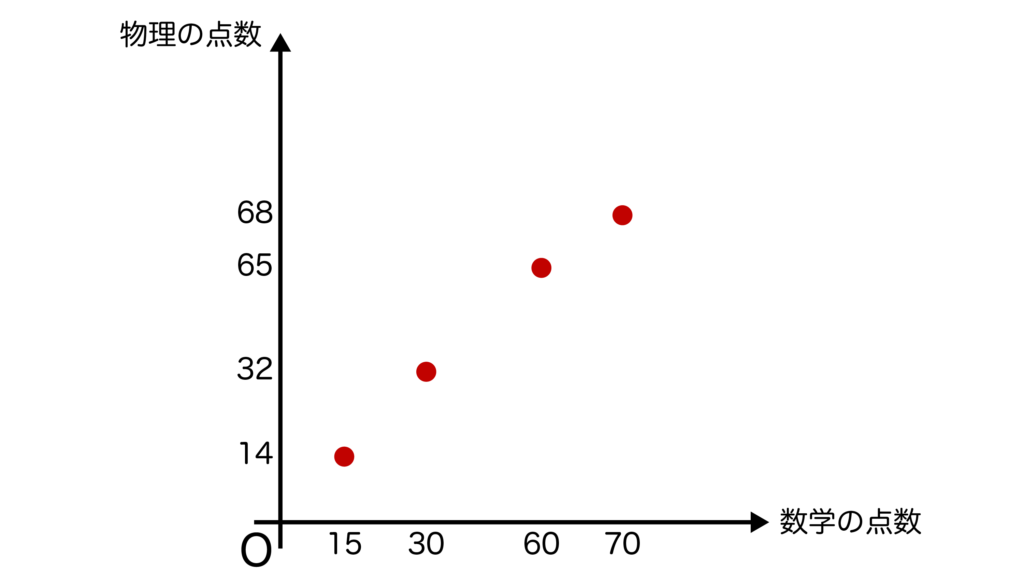
以上で散布図は作成完了です。とても簡単だったと思います。
散布図が書けたところで、ここからは散布図の見方について解説します。
上記の散布図を見てみると、全体的に右上がりの直線のようになっていることがわかりますね。
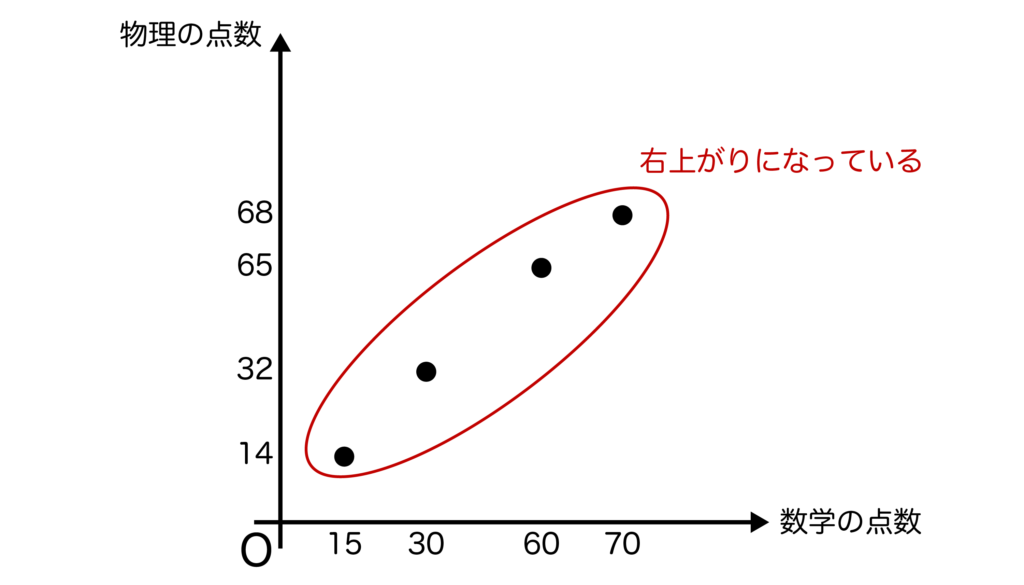
これは数学の点数と物理の点数の関連が強いということを意味しています。
つまり、数学の点数が高ければ、物理の点数も高くなる傾向にあるということです。
以上のように、一方の変量(今回の場合は数学の点数)が増えるともう一方の変量(今回の場合は物理の点数)も増える傾向があることを2つのデータの間に「正の相関がある」といいます。
逆に、一方の変量が増えるともう一方の変量が減る傾向があることを2つのデータの間に「負の相関がある」といいます。
負の相関がある場合の散布図は以下のように右下がりの直線のようになります。
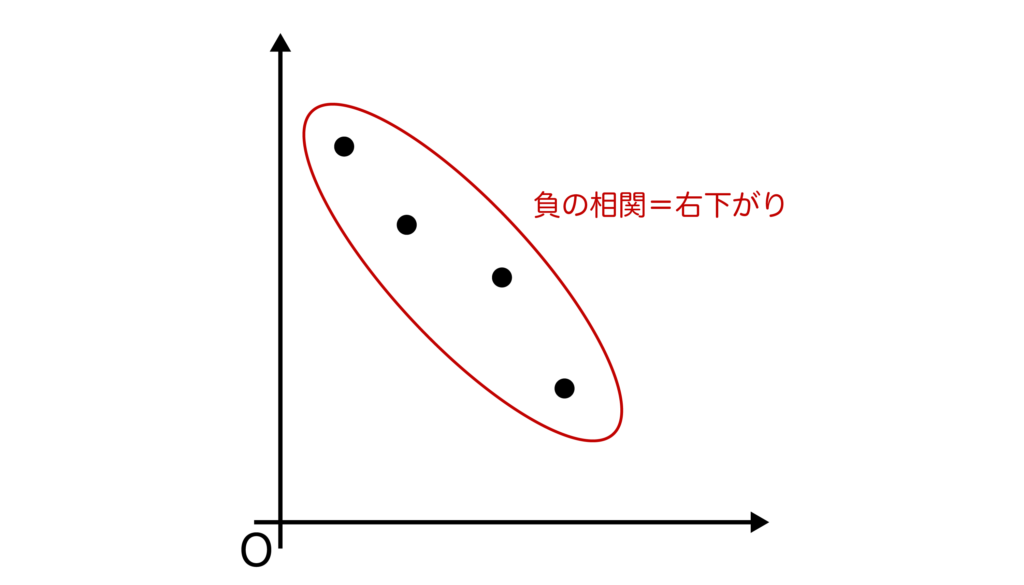
散布図の書き方・見方(相関がない場合)
以上で正の相関と負の相関をご紹介しましたが、相関がない場合もあるので注意が必要です。
以下の例題を見てみましょう。
【例題】
以下の表は高校生5人の100m走のタイムと数学のテストの点数を一覧にしたものである。以下のデータをもとにして散布図を書きなさい。
| A君 | B君 | C君 | D君 | E君 | |
|---|---|---|---|---|---|
| 100m走のタイム[秒] | 16 | 14 | 17 | 20 | 15 |
| 数学の点数[点] | 76 | 40 | 59 | 80 | 90 |
【解答&解説】
先ほどと同じように、まずは座標平面上に横軸:数学の点数、縦軸:100m走のタイムを取ってみましょう。
そして、5人のデータを図示していくと以下のようになりますね。
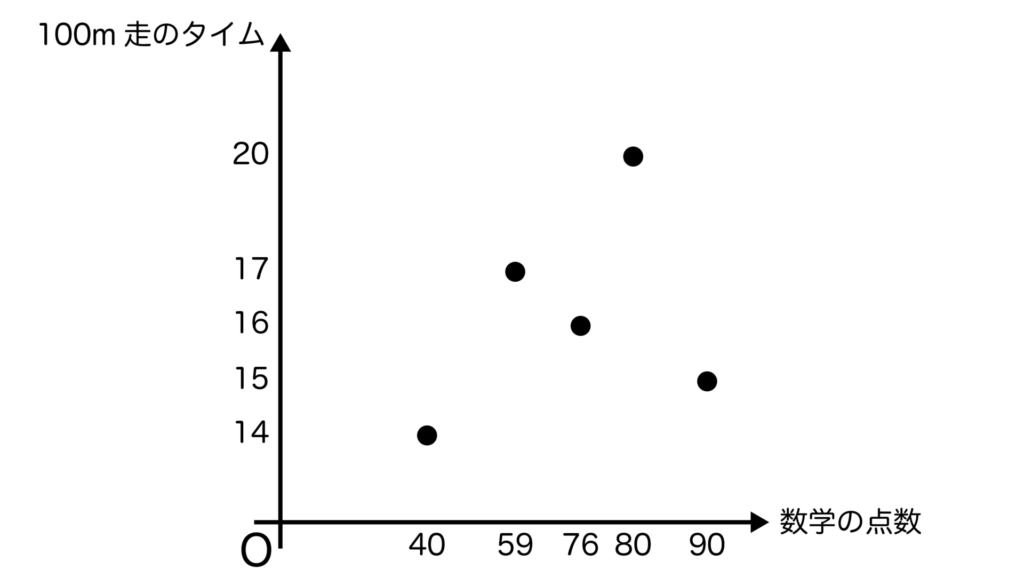
以上の散布図は正の相関や負の相関のときの散布図のように直線状になっておらず、バラバラになっていることがわかります。
これは数学の点数と100m走のタイムの関連が弱いことを意味しています。
以上のように、正の相関や負の相関がない場合は「相関がない」といいます。
散布図では必ずしも正の相関もしくは負の相関が表れるとは限らないのでご注意ください。
そして、以上でご紹介した正の相関と負の相関のようにある変量とある変量が互いに関係し合っていることを相関関係というので必ず覚えておきましょう。
※相関関係の求め方・公式について解説した記事もぜひ合わせてご覧ください。
散布図と強い・弱い正の相関関係/強い・弱い負の相関関係
以下2つの散布図はともに右上がりの直線状なので正の相関があるといえます。
しかし、散布図1の方が散布図2よりもより直線に近いですね。つまり、散布図1の方が1つの直線の近くにデータが集まる度合いが強いといえます。
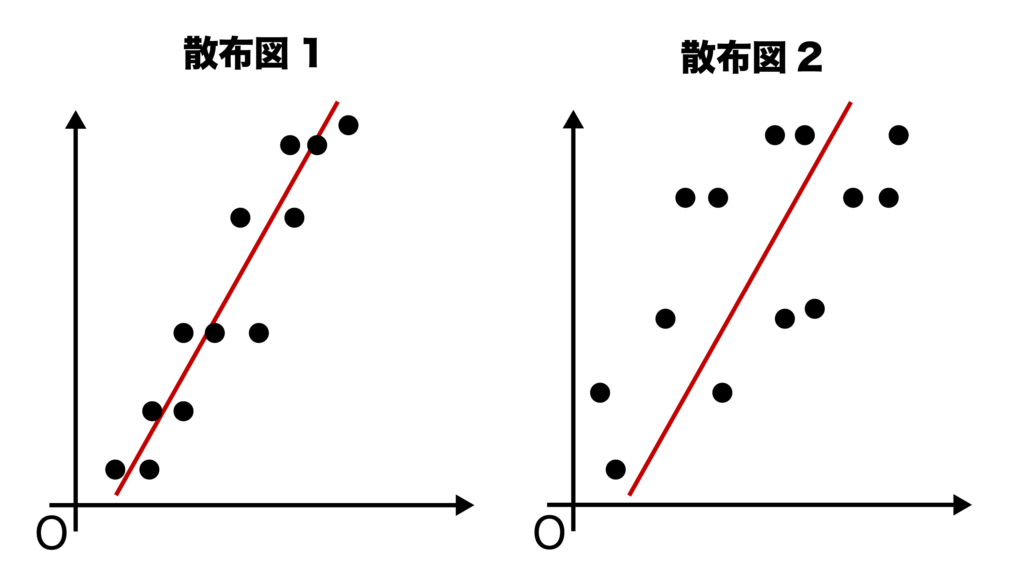
この散布図1のように、1つの直線の近くにデータが集まる度合いが強いことを「強い正の相関がある」といいます。
一方で、散布図2のように1つの直線の近くにデータが集まる度合いが弱いことを「弱い正の相関がある」といいます。
正の相関だけでなく、負の相関に関しても強弱がある(強い負の相関・弱い負の相関)ので覚えておきましょう。
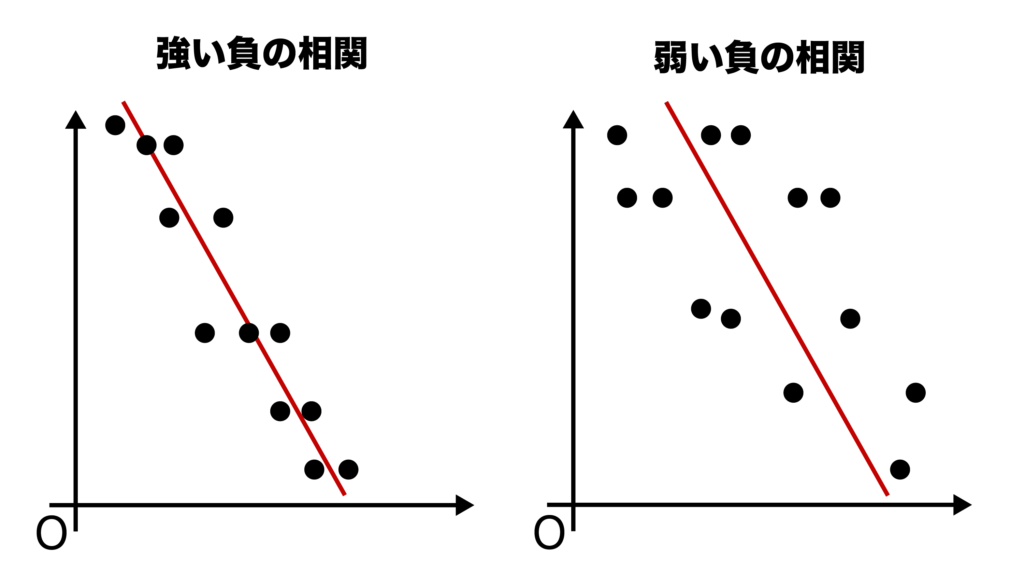
本記事では相関の正負や強弱は散布図の見た目で判断していますが、場合によっては見た目では判断が難しいときもあります。
そのようなときは相関の正負や強弱を計算して判断することも可能です。その数値は相関係数と呼ばれています。
散布図と相関関係・因果関係
散布図を見るときに注意したいこととしては以下の2つがあげられます。
1つ目は、散布図から分析した傾向や相関関係はあくまでも活用したデータに対して言えることであるということです。
例えば、Aという学校で実施された数学のテストの点数と物理のテストの点数の相関関係を調べたところ、数学のテストの点数と物理のテストの点数には正の相関があったとします。
しかし、それはあくまでもAという学校内での話であって、日本の学校全体に対する傾向とするには無理があるということです。
2つ目は相関関係と因果関係を混同しないことです。
因果関係とはいくつかの事柄の関係において、一方が原因で他方が結果であるというつながりのあることです。
「原因」と「結果」がセットになっていることがポイントです。
例えば「テスト3日前の勉強時間」と「テストの点数」に正の相関が認められたとします(=テスト3日前の勉強時間が多いほどテストの点数が高い)
これについては因果関係も認められます。つまり「テストの点数が高い」という結果は「テスト3日前にたくさん勉強した」という原因によって発生していると考えられるからです。
では、「1月に夕食に鍋を食べた世帯」と「1月にインフルエンザになった人の人数」はどうでしょうか?
「1月に夕食に鍋を食べた世帯」と「1月にインフルエンザになった人の人数」には正の相関があるとしましょう(1月は寒いので、夕食に鍋を食べる世帯は多そうですね。また、1月はインフルエンザの季節なのでインフルエンザにかかる人も多そうです)
しかし、「1月に夕食に鍋を食べた世帯」と「1月にインフルエンザになった人の人数」に因果関係があるとは考えられません。
「インフルエンザになった」という結果の原因は「夕食に鍋を食べた」ことであるとは考えにくいからです。
「インフルエンザになった」という結果の原因は「冬(1月)になったことによって風邪が流行しやすくなったから」と考えるのが自然でしょう。
以上のように、相関関係があるからといって因果関係もあるとは限らないのでご注意ください。
いかがでしたでしょうか?
今回は散布図とは何かについて解説した後、散布図の書き方や見方、相関関係と因果関係についても解説しました。
特に相関関係と因果関係の理解は社会に出てからも役に立ちますが、大人でも理解できていない人が多いです。高校生のときにしっかりと理解しておきましょう。


