高校数学の数学Aにおける確率の分野では「同様に確からしい」という用語が登場します。
皆様はこの「同様に確からしい」という用語の意味を説明できますでしょうか?
「同様に確からしい」とは何か・意味を理解するには確率に関する基礎的な用語も必ず理解しておかなければなりません。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が同様に確からしいとは何か・意味について確率の基礎的な用語もおさらいしながら解説していきます。
例題も使ってわかりやすく解説しているので、数学が苦手な人もぜひご覧ください。
同様に確からしいとは?意味は?例題で解説
同様に確からしいとは何か・意味について説明する前に、まずは確率に関する以下の基本的な用語の意味を理解しましょう。
- 試行
- 事象
- 全事象
- 根元事象
まずは試行からですが、試行とは同じ状態のもとで繰り返すことができ、その結果が偶然によって決まる実験や観測のことです。
例としては、サイコロを振ることやくじを引くことなどがあげられます。
サイコロを振ること自体は何回でもできますし、くじを引くことも何回でもできますね(=同じ状態のもとで繰り返すことができる)
また、サイコロを振って何の目が出るかは完全に運ですし、くじを引いて何が出るかも完全に運(=結果が偶然によって決まる)です。
※くじ引きの確率と計算について詳しく解説した記事もぜひ合わせてご覧ください。
そして、試行の結果起こる事柄のことを事象といいます。
ある試行において、起こりうる場合全体の集合をUとすると、この試行におけるどの事象もUの部分集合で表すことが可能です。
※部分集合がわからない人は集合の記号一覧と読み方について解説した記事をご覧ください。
特に、全体集合Uで表される事象を全事象といいます。また、Uの1個の要素からなる集合で表される事象を根元事象といいます。
言葉だけで説明しても理解しにくいと思うので例で解説します。例えば、1つのサイコロを投げるという試行において、2の倍数の目が出る事象をAとすると、
- 全事象U={1、2、3、4、5、6}
- 事象A={2、4、6}
- 根元事象={1}、{2}、{3}、{4}、{5}、{6}
となります。
そして、同様に確からしいとは根元事象のどれが起こることも同じ程度に期待できることです。
上記で1つのサイコロを投げるという試行において根元事象={1}、{2}、{3}、{4}、{5}、{6}であると解説しました。
このとき、
- 1が出る確率
- 2が出る確率
- 3が出る確率
- 4が出る確率
- 5が出る確率
- 6が出る確率
はすべて1/6ですね。「1の目だけ他の目よりも出やすくなっている」「4の目は一番出にくい」などはないわけです。
確率では、起こりうるすべての場合について同様に確からしいことが前提にあります。そのためには、見た目が全く同じものでも区別して考えることがポイントとなります。
※サイコロの確率の計算について詳しく解説した記事もぜひ合わせてご覧ください。
例えば、赤玉1個と白玉4個が入った箱の中から1個の玉を取り出すことを考えてみましょう。
このとき、取り出される玉の色は赤または白のどちらかなので、赤玉が取り出される確率=1/2であるという説明があったとき、ほとんどの人は違和感を覚えるでしょう。
白玉の方が赤玉よりも多いので、圧倒的に白玉の方が出やすいと考えるのが自然だと思います。
確率においては白玉9個の見た目がすべて同じだったとしても、白玉を区別して考えます。
白玉4個をすべて白1、白2、白3、白4のように区別して考えることで、
全事象U={白1、白2、白3、白4、赤}
となり、どの根元事象も同じ程度に起こることが期待できるようになるのです。
つまり、全事象Uの要素の個数n(U)=5より、赤玉が出る確率は1/2ではなく1/5となるのです。
「同様に確からしい」を意識しながら問題を解いてみよう
ここからは、超基礎的な確率の問題を2問ご紹介します。「同様に確からしい」を意識しながら解いてみましょう。
【問題】
(1)2個のサイコロを投げるとき、出る目の和が素数である確率を求めよ。
(2)3枚の硬貨を投げて、表2枚、裏1枚が出る確率を求めよ。
【解答&解説】
(1)同様に確からしいことを意識すると、2個のサイコロをA・Bなどと区別する必要があります。
2個のサイコロを投げる問題では、以下のような表を作ると解きやすいのでテクニックの1つとして覚えておきましょう。
| 和 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
すると、全事象Uについてn(U)=36であることがわかります。
目の和が素数2、3、5、7、11になるのは、表の通りそれぞれ
1、2、4、6、2[通り]あり、合計=1+2+4+6+2=15[通り]ですね。
それぞれの根元事象が起こることは同じ程度に期待できる(=同様に確からしい)ので、15/36=5/12・・・(答)となります。
※素数とは何かについて解説した記事もぜひ参考にしてください。
(2)同様に確からしいことを意識すると、3枚の硬貨をA・B・Cなどと区別する必要があります。
区別することによって、以下の図から全事象n(U)=8であることがわかります。
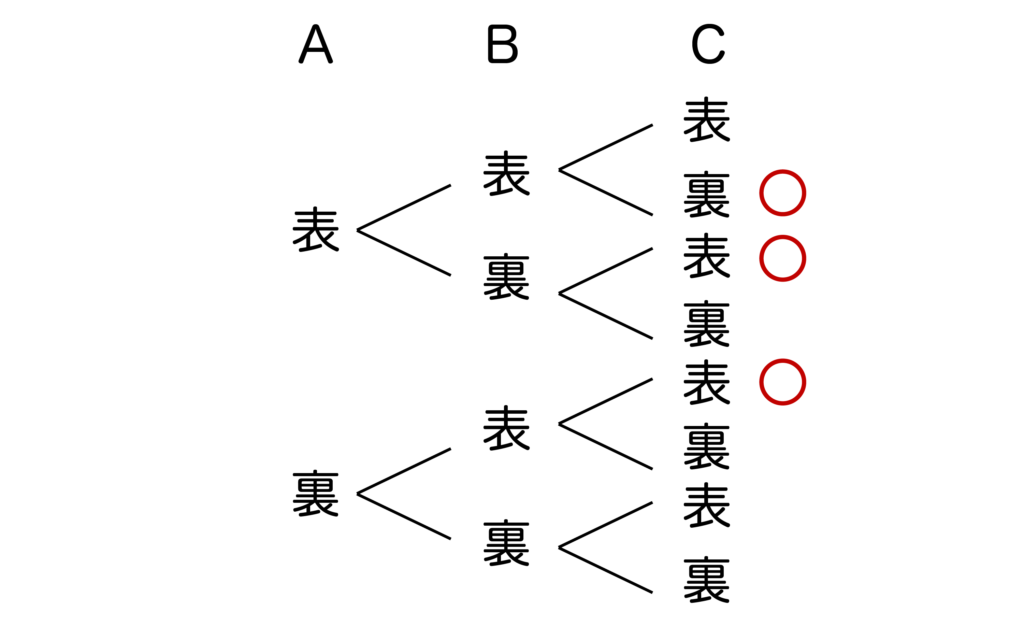
表2枚、裏1枚が出るパターンは上記の通り3通りなので、答えは3/8・・・(答)となります。
※コインの確率の計算について詳しく解説した記事もぜひ合わせてご覧ください。
いかがでしたでしょうか?
今回は同様に確からしいとは何か・意味について解説していきました。同様に確からしいという用語は確率や場合の数の問題を解く上ではあまり意識しなくても大丈夫です。
意識しすぎるとかえって混乱してしまう人もいるからです。混乱しそうであれば、本記事の内容はサクッと忘れても問題ありません。