高校数学の数学Aで苦手とする人が多いのが場合の数における組み合わせです。
組み合わせは後ほど詳しく解説しましが、Cを使った計算になります。
今回は早稲田大学教育学部数学科を卒業した筆者が組み合わせCの計算方法と公式をご紹介した後、例題とともに組み合わせの解法パータンについてわかりやすく解説していきます。
数学が苦手・場合の数が苦手な人はぜひご覧ください。
組み合わせとは?順列との違い
まずは組み合わせとは何かについて解説します。
例えば、4つの数字1、2、3、4の中から異なる3つを選んで一列に並べる順列では、その並べる順序を考慮していました。
なので、例えば123と321は別物とみなしました。
※詳しくは順列とは何かについて解説した記事をご覧ください。
しかし、組み合わせは順列とは違って並べる順序は考慮しません。つまり、123と321は同じものとみなします。
なので、4つの数字1、2、3、4の中から異なる3つを選ぶ方法(=組み合わせ)を辞書式配列法で考えると、
(1、2、3)(1、2、4)(1、3、4)(2、3、4)
の4通りとなります。
※辞書式配列法とは何かについて解説した記事もぜひ合わせてご覧ください。
組み合わせCの計算方法と公式
一般に、r≦nのとき、異なるn個のものの中から異なるr個を取り出し、順序は考慮しないで1組としたものをn個からr個取る組み合わせといい、その組み合わせの総数をnCrで表現します。
※記号「≦」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。
Cは英語で「組み合わせ」を意味する「Combination」の頭文字を取ったものです。
例えば、先ほどご紹介した4つの数字1、2、3、4の中から異なる3つを選ぶ方法(=組み合わせ)は4C3=4と表現することができます。
nCr
=nPr/r!
=n(n-1)(n-2)・・・(n-r+1)/r(r-1)・・・3・2・1
=n!/r!(n-r)!
となります。以上が組み合わせCの公式となりますが、覚える必要はありません。
例えば、先ほどの4C3=4・3・2/3・2・1=4となります。
nCrではr!が分母にきて、nPrが分子にくるだけの話です。
例えば、
- 5C2=5・4/2・1=10
- 10C4=10・9・8・7/4・3・2・1=210
となります。
組み合わせCの計算をたくさんこなしていけば自然に身についているので、無理に文字の入った複雑な公式を覚える必要はありません。
組み合わせCの計算の性質
組み合わせCの計算の性質として以下の4つを覚えておきましょう。
- nCn=1
- nC0=1
- nCr=nCn-r(0≦r≦n)
- nCr=n-1Cr-1+n-1Cr(1≦r≦n-1、n≧2)
それぞれ順番に解説していきます。
まずはnCn=1からです。これはあえて暗記するまでもありません。
例えば、3C3=3・2・1/3・2・1となるので1となります。
続いてはnC0=1です。順列においてはnP0=1と定めていましたね。これと同じ要領で組み合わせにおいてはnC0=1と定めます。これは暗記しておきましょう。
続いてはnCr=nCn-r(0≦r≦n)です。
例えば、6C4=6C2となります。2は6-4からきています。
6C4=6・5・4・3/4・3・2・1=15ですね。
一方で、6C2=6・5/2・1=15であり確かに6C4と一致していることがわかります。
nCr=nCn-rが成り立つ理由としては、n個からr個取ることは、n個からn-r個残すことと同じであるためです。
この公式は組み合わせの計算を楽にするものなので、必ず覚えておきましょう。
最後はnCr=n-1Cr-1+n-1Cr(1≦r≦n-1、n≧2)です。
例えば、7C3=7・6・5/3・2・1=35・・・(※)ですね。
7C3を上記の公式に適用すると、
7C3
=7-1C3-1+7-1C3
=6C2+6C3
=6・5/2・1+6・5・4/3・2・1
=15+20
=35
となり、確かに※と一致していることがわかります。
この公式は使う機会はめったにないので、無理して覚える必要はありません。
組み合わせの基本問題
組み合わせCの意味や計算方法・公式がわかったところで、ここからは組み合わせの問題をどんどん解いていきましょう。
まずは基本問題からです。
【問題1】
次の値を求めよ。
(1)8C3
(2)11C10
【解答&解説】
(1)8C3=8・7・6/3・2・1=56・・・(答)
(2)11C10=11C1=11・・・(答)
※nCrのとき、rとn-rを比べて、n-r<rの場合はnCn-rを計算した方がnCrを求めるよりも楽です。ぜひこれからの組み合わせの計算で意識してみてください。
【問題2】
男子3人、女子4人から3人を選ぶ。このとき、以下の問いに答えよ。
(1)7人から3人を選ぶ選び方は全部で何通りあるか。
(2)3人のうち、女子が1人だけ入るようにする選び方は全部で何通りあるか。
(3)3人のうち、女子が少なくとも1人入っている選び方は全部で何通りあるか。
【解答&解説】
(1)7C3=7・6・5/3・2・1=35[通り]・・・(答)
(2)女子が1人だけ入るということは男子は2人です。
男子3人から2人を選ぶ選び方は3C2=3C1=3[通り]ですね。
そのおのおのに対して、女子4人から1人選ぶ選び方は4C1=4[通り]なので、
3・4=12[通り]・・・(答)となります。
(3)「少なくとも」という言葉が問題文に出てきたときは余事象を疑いましょう。
女子が少なくとも1人入っている=(すべての選び方)ー(全員男子)
ですね。
すべて男子を選ぶ(全員男子)選び方=3C3=1[通り]です。
すべての選び方は(1)より35通りなので、35-1=34[通り]・・・(答)となります。
※余事象とは何かについて解説した記事もぜひ合わせてご覧ください。
線分・三角形の個数と組み合わせに関する問題
【問題1】
正七角形について以下の数を求めよ。
(1)3個の頂点を結んでできる三角形の個数
(2)対角線の本数
(3)正七角形と2辺を共有する三角形の個数
【解答&解説】
(1)7個の頂点から3個を選んで線分で結ぶと三角形が1個できるので、
7C3=7・6・5/3・2・1=35[個]・・・(答)
(2)正七角形の2個の頂点を結ぶ線分の本数は、
7C2=7・6/2・1=21[本]
対角線の本数は、これから正七角形の辺の数を除いたものなので、21-7=14[本]・・・(答)
(3)正七角形と2辺を共有する三角形は正七角形の頂点の個数だけあるので、7[個]・・・(答)
【問題2】
正n角形A1A2A3・・・Anの頂点を結んでできる三角形のうち、正n角形と辺を共有しない三角形の個数を求めなさい。ただし、nは5以上とする。
【解答&解説】
正n角形の頂点を結んでできる三角形の個数はnC3[個]ですね。
そのうち、正n角形と1辺だけを共有する三角形はn≧5のときn(n-4)個あり、2辺を共有する三角形はn個あるから、正n角形と辺を共有しない三角形の個数は、
nC3-n(n-4)-n
=n(n-1)(n-2)/3・2・1-n(n-4)-n
=n(n-4)(n-5)/6[個]・・・(答)となります。
組み合わせを利用した組分けに関する問題
【問題】
9人の学生を以下のように分ける方法は全部で何通りあるか求めよ。
(1)4人、3人、2人の3組に分ける。
(2)3人ずつA、B、Cの組に分ける。
(3)3人ずつ3組に分ける。
【解答&解説】
(1)9人から4人を選んで、残りの5人から3人を選べば自動的に残りの2人は決まるので、
9C4・5C3=126・10=1260[通り]・・・(答)
(2)Aに入れる3人選ぶ方法=9C3=84[通り]
Bに入れる3人を残りの6人から選ぶ方法=6C3=20[通り]
AとBが決まればCは自動的に決まるので、
84・20=1680[通り]・・・(答)
(3)(2)においてA・B・Cの区別をなくすと、同じものが3!通りずつできるので、分け方の総数は
(84・20)/3!=1680/6=280[通り]・・・(答)となります。
組分けの問題では、以下を明確にしておくのがポイントです。
- 分けるものが区別できるかどうか
- 分けてできる組が区別できるかどうか
今回の場合、9人の学生はそれぞれ別の人間なので区別できます。
(1)における3組は人数の違いから区別可能です。
(2)においては組にA、B、Cという名称が振られているので区別可能です。
(3)においては人数が同じなので区別不可です。なので、(2)においてA・B・Cの区別をなくす必要があります。
塗り分けに関する組み合わせの問題
【問題】
以下の図のように、4つに分けた円を隣り合う箇所は異なる色で塗り分けたい。ただし、円を回転させて一致する塗り方は同じものとみなす。このとき、以下の問いに答えよ。
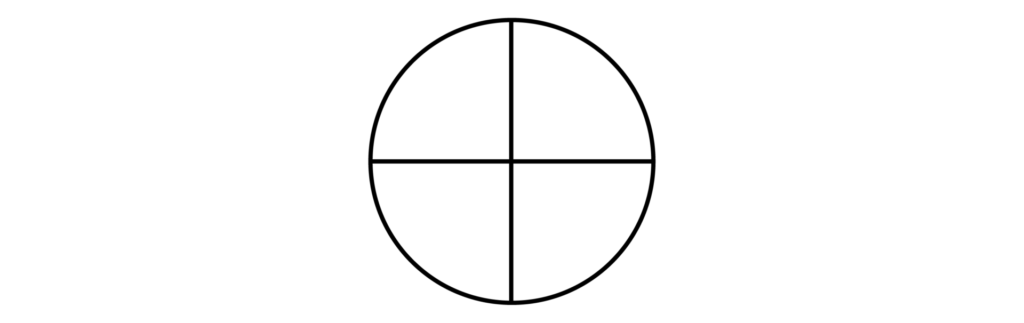
(1)赤・青・緑・紫の4色から2色を選んで塗り分ける方法は全部で何通りあるか求めよ。
(2)赤・青・緑・紫の4色から3色を選び、その3色すべてを使って塗り分ける方法は全部で何通りあるか求めよ。
【解答&解説】
(1)「隣り合う箇所は異なる色で塗り分る」という条件があるので、以下のようにアとイの色を決めれば良いことがわかります。選んだ2色で塗り方が1通りに決まります。
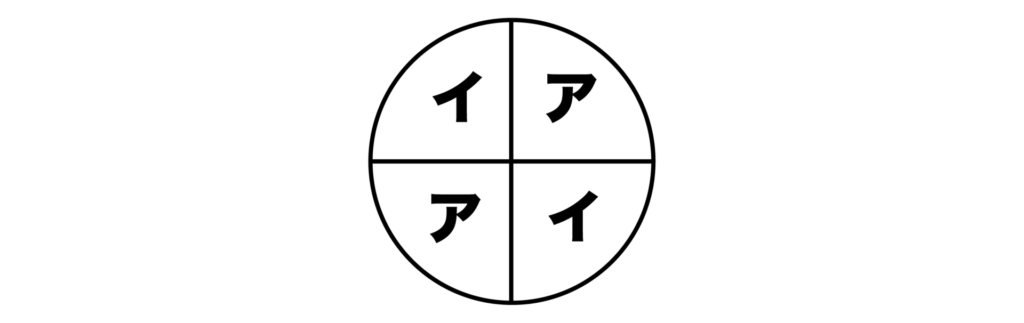
よって、2色の選び方が求める場合の数なので、4C2=6[通り]・・・(答)となります。
(2)3色を使って塗り分けるには、以下のように1色で2箇所を塗り、残り2色は1箇所ずつ塗れば良いことがわかります。
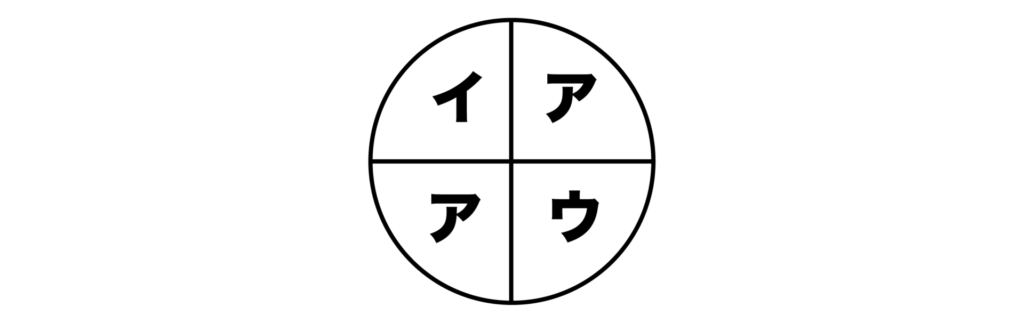
塗り分け方は2箇所を塗る色の選び方と同じなので、3C1=3[通り]となります。
また、3色の選び方=4C3=4[通り]です。
よって3・4=12[通り]・・・(答)となります。
【補足】重複組み合わせについて
組み合わせの文脈で、重複組み合わせについて簡単にご紹介して本記事を終了とします。
重複組み合わせとは異なるn個のものから重複を許してr個取る組み合わせのことです。
重複組み合わせはHで表現され、重複組み合わせの総数はnHr=n+r-1Crとなります(n<rでもOKです)
では、例題を1つ解いてみましょう。
【例題】
メロン、ミカン、リンゴが店頭にたくさんおいてある。この中から5つを購入するとき、何通りの買い方があるか求めよ。ただし、1個も購入しないものがあっても良いものとする。
【解答&解説】
買い物かごの中に2個の仕切り(|)を入れて、一番左側にはメロン、真ん中にはミカン、右側にはリンゴを入れるとする。
例としては以下の図のようになります。

以上のように考えると、5個の◯と2個の|の順列の総数が、3種類の果物から5個を購入する買い方の総数に一致します。
これは同じものを含む順列で3+5-1=7個の場所から5個の◯の場所を選ぶ組み合わせの数に等しくなります。
よって、3+5-1C5=7C5=7C2=21[通り]・・・(答)となります。
いかがでしたでしょうか?
今回は組み合わせCの計算方法と公式、組み合わせの問題をご紹介していきました。
組み合わせは順列と見分け方がつかない人も多いですが、たくさんの問題を解いていくうちに慣れていきます。ぜひ教科書や参考書、問題集などでたくさんの組み合わせ・順列の問題を解くことを意識してみてください。