今回は高校数学の数学Aにおける順列を取り上げます。順列はアルファベットの「P」で表現されます。
順列は場合の数を求めるための王道的な方法の1つで、大学入試や共通テストでも頻出なので必ずマスターしておきましょう。
今回は早稲田大学教育学部数学科を卒業した筆者が順列Pとは何か?や計算方法や公式のご紹介だけでなく、順列の公式が成り立つ理由(証明)、順列Pと組み合わせCの違い、順列で必ず解いておきたい問題などもご紹介します。
かなり盛りだくさんの内容になっているので、ぜひ最後までお読みいただき、順列の理解を深めてください。
順列Pとは?計算方法や公式
まずは順列とは何かについて解説していきます。
順列とは、異なるn個のものの中から異なるr個を取り出して1列に並べる場合の数のことをいいます。
以上を数式で表現すると、
nPr=n(n-1)(n-2)・・・(n-r+1)=n! / (n-r)!となります。
順列は英語で「permutation」と呼ばれており、頭文字を取って「P」で表現されることが多いです。
例えば、
5P3=5・(5-1)・(5-2)=5・4・3=60となります。
5→4→3と1つずつ数字が下がっていっているだけですね。
5P3をnPrに当てはめると、n=5、r=3であり、順列ではrの数(今回は3)だけ掛け算を行います。
また、nPnはn!と表現され、
n!=n(n-1)(n-2)・・・3・2・1となります。
以上を踏まえると、
- 5!=5・4・3・2・1=120
- (5-3)!=2!=2・1=2
となります。こちらも単純に1つずつ数字が下がっていき、「!」の計算では1まですべて掛け算を行います。
以上より、5! / (5-3)!=120/2=60となり、確かに上記の5P3=5・(5-1)・(5-2)と一致していることが確認できます。
以上が順列Pの計算方法・公式となります。
nPr=n(n-1)(n-2)・・・(n-r-1)=n! / (n-r)!は覚えなくても、単純に数字がrの個数だけ1つずつ下に下がることだけ覚えておけば問題ありません。
ちなみにですが、数学Aの順列においては0!=1、nP0=1と定めますので、これだけはしっかりと覚えておきましょう。
順列Pとは?計算方法・公式の証明
ここからは
nPr=n(n-1)(n-2)・・・(n-r+1)=n! / (n-r)!となる理由(証明)について解説していきます。
まず前提知識として、r≦nのとき、異なるn個のものの中から異なるr個を取って1列に並べる順列を、「n個からr個取る順列」といいます。
※記号「≦」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。
【証明】
nPrは、
- 1番目のものの取り方=n通り
- 2番目のものは、残りのn-1個の中から1つ取るので、取り方=n-1通り
- 3番目のものは、残りのn-2個の中から1つ取るので、取り方=n-2通り
以上のようにして、最後のr番目のものはすでに取ったr-1個を除いた残りn-(r-1)個の中から1つ取るので、取り方=n-(r-1)通りとなりますね。つまり、n-r+1通りです。
したがって、求める順列の総数nPrは、積の法則より
nPr=n(n-1)(n-2)・・・(n-r+1)となることがわかります。
※積の法則がわからない人は、積の法則とは何かについて解説した記事をご覧ください。
【証明終】
順列の公式の証明は大学入試や共通テストで出題されることはないと考えて問題ありません。
なので、無理に証明を暗記する必要はありませんのでご安心ください。
順列の例題
では、以上でご紹介した順列の計算方法・公式を使って順列に関する問題を1つ解いてみましょう。
【例題】
3つの異なる文字a、b、cから異なる2つを取って1列に並べる方法は何通りあるか求めなさい。
【解答&解説】
- 1番目の取り方は3通り
- 2番目の取り方は2通り
ですね。よって、求める順列の総数は3P2=3・2=6[通り]・・・(答)となります。
念のため、辞書式配列法を使って検算してみましょう。
a、b、cから2つを取る場合の数は、ab、ac、ba、bc、ca、cbの確かに6通りであることが確認できますね。
※辞書式配列法がわからない人は辞書式配列法とは何かについて解説した記事をご覧ください。
順列は「一列に並べる」というのがポイントです。なので、「ab」と「ba」は別物とみなしますのでご注意ください。
順列の基本問題(数字の順列)
順列では非常に多様な問題を用意することが可能です。
というわけでここからは、順列に関する代表的な問題を順番にご紹介していきます。
まずは基本問題として数字の順列に関する問題を解いてみましょう。
【問題】
6個の数字1、2、3、4、5、6の中から3個を選んで一列に並べるとき、できる3桁の整数は全部で(ア)個あり、このうち偶数は(イ)個ある。また、4の倍数は(ウ)個ある。
(ア)〜(ウ)に入る数を求めよ。
【解答&解説】
(ア)求める個数は異なる6個の数から3個を取って並べる順列の総数なので、
6P3=6・5・4=120・・・(答)となります。
(イ)偶数であるということは一の位が2、4、6のいずれかになりますね(3通り)
そのおのおのに対して百、十の位は残り5個から2個を取って並べる順列なので5P2=5・4=20[通り]です。
したがって、3・20=60・・・(答)となります。
(ウ)下2桁が4の倍数であれば、その数は4の倍数となります。
そのような数は12、16、24、32、36、52、56、64の8通りありますね。
百の位は下2桁以外の整数であれば良いので、8・4=32・・・(答)となります。
※様々な倍数の判定法をご紹介した記事もご用意しているので、ぜひ参考にしてください。
0を含む数字の順列の問題
続いては0を含む数字の順列の問題です。
0があることによって先頭の位に0を持ってくることができなくなることにご注意ください。
【問題】
0、1、2、3、4、5の6個の数字から異なる4個の数字を取って並べ、4桁の整数を作るとき、以下のものは全部で何個できるか答えよ。
(1)整数
(2)3の倍数
【解答&解説】
(1)まず、千の位は0以外の1〜5から1個を取るので5[通り]です。
そのおのおのについて百、十、一の位は0を含めた残りの5個から3個を取る順列となるので、
5P3=5・4・3=60[通り]となります。
よって答えは5・60=300[通り]・・・(答)となります。
(2)各位の数の和が3の倍数であれば、その数は3の倍数となります。
※例として396をみてみましょう。各位の数の和=3+9+6=18で3の倍数になっています。また、396は3で割り切れるので、確かに3の倍数であることが確認できます。
0、1、2、3、4、5のうち和が3の倍数になる4個の数字の組は
- (0、1、2、3)
- (0、1、3、5)
- (0、2、3、4)
- (0、3、4、5)
- (1、2、4、5)
の5通りですね。
[1]0を含む4組について
1つの組について、千の位は0以外なので、3・3!=3・3・2・1=18[個]となります。
よって、4・18=72[個]となります。
[2](1、2、4、5)について
整数の個数は4!=4・3・2・1=24[個]となります。
[1]と[2]より、求める個数は72+24=96[個]・・・(答)となります。
隣接する順列としない順列の問題
【問題】
男性A・B・C、女性D・E・F・Gの7人が1列に並ぶことを考える。
このとき、以下の(1)〜(3)に答えよ。
(1)AとBが隣り合うような並び方は何通りあるか求めよ。
(2)AとBが両端にくるような並び方は何通りあるか求めよ。
(3)どの男性も隣り合わないような並び方は何通りあるか求めよ。
【解答&解説】
(1)隣り合う場合は、2人を1組と考えるのが定石です。今回の場合はAとBを1組(1人)と考えます。
A・Bの2人1組と残り5人の並び方=6!=6・5・4・3・2・1=720[通り]です。
そのおのおのについてA・Bの並び方=2!=2[通り]です。
したがって、720・2=1440[通り]・・・(答)となります。
(2)AとBが両端に並ぶ並び方=2!=2[通り]です。
そのおのおのについて、残りの5人の並び方は5!=5・4・3・2・1=120[通り]です。
よって、2・120=240[通り]・・・(答)となります。
(3)まずは女性4人を並べる→その間または端に男性を並べるという手順で解いていきましょう。
女性4人の並び方=4!=4・3・2・1=24[通り]ですね。
そのおのおのについて、女性4人の間または両端の5箇所に男性3人を並べる方法=5P3=5・4・3=60[通り]です。
よって、24・60=1440[通り]・・・(答)となります。
この問題に似た問題は大学入試や共通テストでも出題頻度が高いので、必ずできるようにしておきましょう。
辞書式に並べる順列の問題
【問題】
アルファベットA・B・C・D・Eを辞書式に並べることを考える。
1番目はABCDEF、2番目はABCED・・・となる。このとき、39番目の並びはどうなるか求めよ。
【解答&解説】
A□□□□の形のものは4!=24[個]ありますね。
BA□□□の形のものは3!=6[個]ありますね。
BC□□□の形のものは3!=6[個]ありますね。
BDA□□の形のものは2!=2[個]ありますね。
ここまでで24+6+6+2=38[個]です。
38番目はBDAECなので、39番目はBDCAE・・・(答)となります。
辞書式に並べる順列の問題では左側から順番に文字を決めて個数を調べていくのが定石です。必ず覚えておきましょう。
完全順列の問題
【問題】
5人の友達に手紙を封筒に入れて送ることを考える。宛名を書いた手紙と、それを入れる宛名を書いた封筒の合計10枚を作成した。
このとき、手紙をすべて間違った封筒に入れる方法は何通りあるか求めよ。
【解答&解説】
5人の友達を1、2、3、4、5とします。
すると、求める場合の数は5人を1列に並べた順列のうち、k番目がk(k=1、2、3、4、5)でないものの個数に等しくなりますね。
1番目が2のとき、条件を満たす順列は以下の11[通り]になりますね。
- 2-1-4-5-3
- 2-1-5-3-4
- 2-3-1-5-4
- 2-3-4-5-1
- 2-3-5-1-4
- 2-4-1-5-3
- 2-4-5-1-3
- 2-4-5-3-1
- 2-5-1-3-4
- 2-5-4-1-3
- 2-5-4-3-1
1番目が3、4、5のときも条件を満たす順列は同様に11通りずつあるので、求める方法は11・4=44[通り]・・・(答)となります。
※以上の問題のように、1〜nのn個の数字を1列に並べた順列のうち、k番目の数字≠kとなるものを完全順列といいます。
塗り分けの順列の問題
【問題】
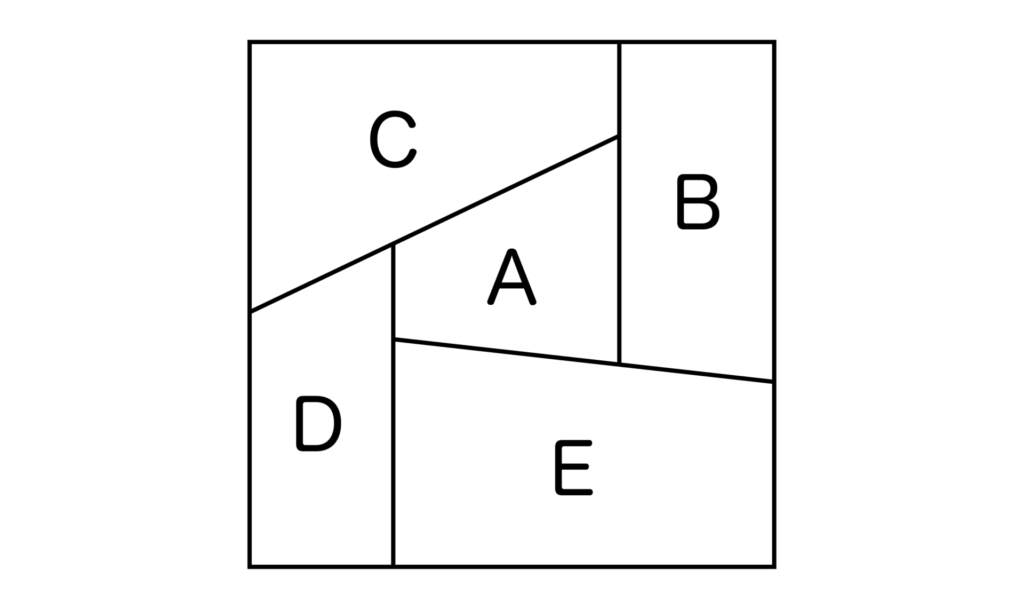
5色の絵の具を使って以下の図におけるA〜Eを塗り分ける。このとき、以下の問いに答えよ。
(1)5色すべてを使う場合、何通りの塗り分け方があるか。
(2)同じ色を何回使っても良いが、隣り合う部分は異なる色とする場合、何通りの塗り分け方があるか。
【解答&解説】
(1)A、B、C、D、Eに塗った色を順に1列に並べると、5色の順列になりますね。
よって、塗り方の総数=5P5=120[通り]・・・(答)となります。
(2)A〜Eを塗り分けるには3色以上必要ですね。
[1]5色使う場合
(1)より120[通り]
[2]4色使う場合
この場合、2箇所が同じに色になります。
その部分はBとDか、CとEの2通り。
そのおのおのに対して、5色から4色を選んで4つの部分に塗る方法=5P4=5・4・3・2・1=120[通り]
したがって、2・120=240[通り]となります。
[3]3色使う場合
A、B、Cはお互いに他の2つと隣り合っているので、この3つの部分で3色が必要となります。
このとき、CはBと同じ色、EはCと同じいろになりますね。
よって、この場合の塗り方=5P3=5・4・3=60[通り]です。
[1]〜[3]より、120+240+60=420[通り]・・・(答)となります。
同じものを含む順列の問題
【問題】
aが4個、bが3個、cが2個ある。このとき、計9個の順列の総数を求めよ。
【解答&解説】
まず、a、b、cがすべて異なるものと考えてa1、a2、a3、a4、b1、b2、b3、c1、c2の9個の順列と考えると、その順列=9![通り]となりますね。
ここで、a1=a2=a3=a4=aとすると、同じものが4![通り]
b1=b2=b3=bとすると、同じものが3![通り]
c1=c2=cとすると、同じものが2![通り]
ずつ登場しますね。よって、求める順列の総数をkとすると、k・4!・3!・2!=9!となるので、
k=9! / (4!3!2!)=1260[通り]・・・(答)となります。
【別解】
以上は順列を活用して求めましたが、組み合わせを使って求めることも可能です。
[1]以下の9個の◯からa4個を入れる位置を決める方法=9C4[通り]
◯◯◯◯◯◯◯◯◯
[2]残りの5個の◯からb3個を入れる位置を決める方法=5C3[通り]
a◯aa◯◯◯◯a
[3]残りの2個の◯にc2個を入れる方法=2C2[通り]
abaa◯bb◯a
よって、9C4・5C3・2C2=1260[通り]・・・(答)となります。
同じ数字を含む順列の問題
【問題】
1、2、3の数字が書かれたカードがそれぞれ2枚、3枚、4枚ある。これらのカードから4枚を使ってできる4桁の整数は全部で何個あるか求めよ。
【解答&解説】
1、2、3のいずれかをA、B、Cで表しましょう。ただし、A、B、Cはすべて異なる数字とします。
[1]AAAAの場合
同じ数字を4つ含むとき、4枚ある数字は3のみなので1個となります。
[2]AAABの場合
同じ数字を3つ含むとき、3枚以上ある数字は2と3なのでAの選び方は2通りですね。
Aにどれを選んでもBの選び方は2通りです。
そのおのおのについて並べ方=4!/3!=4通りです。
したがって、このタイプの整数は2・2・4=16[個]となります。
[3]AABBの場合
同じ数字2つを2組含むとき、1、2、3はすべて2枚以上あるので、A、Bの選び方は3C2[通り]です。
そのおのおのについて並べ方=4!/2!2!=6[通り]です。
よって、このタイプの整数は3C2・6=18[個]となります。
[4]AABCの場合
最後は同じ数字2つを1組含むときです。
Aの選び方は3通りあり、B、CはAを選べば決定しますね。
そのおのおのについて並べ方=4!/2!=12[通り]です。
よって、このタイプの整数は3・12=36[個]となります。
[1]〜[4]より、1+16+18+36=71[個]・・・(答)となります。
順列を使った最短経路に関する問題
【問題】
以下の図のような道において、PからQまで遠回りをしないで行くのに、次の場合の道順の総数を求めよ。
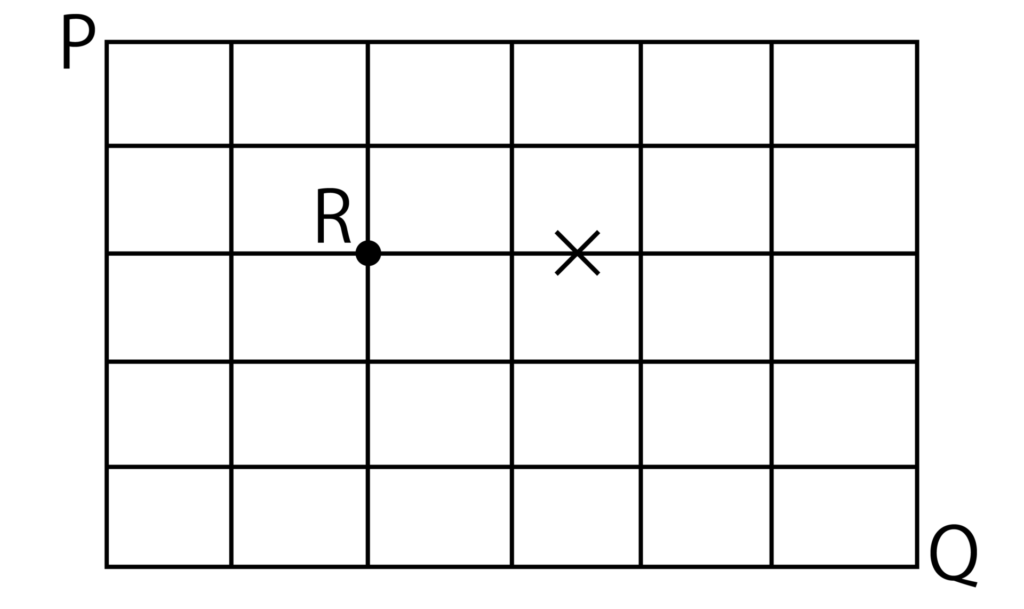
(1)Rを通って行く。
(2)Rを通り、×印の箇所は通らないで行く。
【解答&解説】
(1)右へ1区間進むことを→、下へ1区間進むことを↓で表すとします。
PからRまで行く最短の道順は、→2個と↓2個の順列で表すことができるので、4!/2!2![通り]です。
RからQまで行く最短の順列は、→4個と↓3個の順列で表すことができるので、7!/4!3![通り]です。
したがって、4!/2!2! × 7!/4!3!=210[通り]・・・(答)となります。
(2)Rを通って行く最短の道順の総数から、Rを通り×印の箇所を通って行く道順を除けば良いですね。
Rを通り×印の箇所を通る経路はP→R→A→B→Qなので、
4!/2!2! × 1 × 1 × 5!/2!3!=60[通り]となります。
Rを通って行く最短の道順の総数は(1)より210通りなので、210-60=150[通り]・・・(答)となります。
順序が決まった順列の問題
【問題】
YOKOHAMAの8文字を横一列に並べて順列を作るとき、Y、K、H、Mがこの順に並ぶ順列の数を求めよ。
【解答&解説】
Y、K、H、Mがこの順に並ぶということはY、K、H、Mの並べ替えは考えなくても良いということです。
つまり、Y、K、H、Mを同じもの□として、□4個とO2個、A2個の順列を作り、□にY、K、H、Mの順に入れると考えます。
よって、求める順列の総数=8! / (4!2!2!)=420[通り]・・・(答)となります。
円順列・数珠順列・重複順列
ここからは円順列・じゅず順列・重複順列の3つを簡単にご紹介していきます。
まず円順列からですが、円順列とはいくつかのものを円形に並べる配列のことです。
円順列では、適当に回転させて並びが一致するものは同じものとみなします。
異なるn個のものの円順列の総数=(n-1)!で求めることができます。
詳しくは円順列について解説した記事をご覧ください。
続いて数珠順列です。数珠順列とは首飾りのように、異なるいくつかのものを円形に並べ、回転または裏返して一致するものは同じものとみなすときの並び方のことをいいます。
異なるn個のものの数珠順列の総数=(n-1)! / 2となります。
詳しくは数珠順列について解説した記事をご覧ください。
最後は重複順列です。重複順列とは異なるn個のものから、重複を許してr個を取り出して並べる順列のことです。重複順列の公式はnrとなります。
詳しくは重複順列について解説した記事をご覧ください。
順列と組み合わせの違い・見分け方
最後に順列と組み合わせの違い・見分け方について解説します。
順列は先ほどから解説している通り「一列に並べる」というのがポイントになります。
順列では選ぶときに選んだものの順序まで考えます。
それに対して、組み合わせでは選んだものの順序は考えません。どれとどれを選ぶのかのみに注目します。
例えば、4人の生徒A・B・C・Dから2人を選ぶことを考えてみます。
単に2人を選ぶだけなら4C2=(4・3)/(2・1)=6[通り]です。
A・Bを選ぶのとB・Aを選ぶのは同じことです。つまり、順序は考えていません。
しかし、2人を選んでその2人を前後一列に並べる場合はどうでしょうか?
このときは4P2=4・3=12[通り]となります。
(前、後)=(A、B)と(前、後)=(B、A)では意味が異なるので、同じものとはみなしませんよね。つまり順序を考慮しています。よって、組み合わせではなく順列になります。
順列と組み合わせに迷ったときは、ABとBAを同じとみなすかどうかをぜひ一度考えてみてください。
※組み合わせについて詳しく解説した記事もご用意しているので、ぜひ合わせてご覧ください。
いかがでしたか?
今回は順列Pとは何かについて解説した後、計算方法や公式、証明、順列を活用した様々な問題、順列と組み合わせの違い・見分け方をご紹介しました。
順列は大学入試や共通テストで必ずといっていいほど使います。たくさんの問題を解いて慣れていきましょう。


