三角形の面積の求め方は主に4つあります。中には高校で学習する三角比を活用して三角形の面積を求める方法もあります。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が三角形の面積の求め方の公式を4つ(ヘロンの公式を含む)ご紹介します。
高校生であれば4つすべて知っておくべき内容ですので、必ず最後までお読みください。
三角形の面積の求め方の公式1つ目
三角形の面積の求め方の公式1つ目は基本中の基本とも言える「底辺×高さ×1/2」です。
小学校でも学習する内容なので、高校生であれば必ず知っておかなければなりません。
例えば、以下の三角形ABCの面積を公式を活用して求めてみましょう。
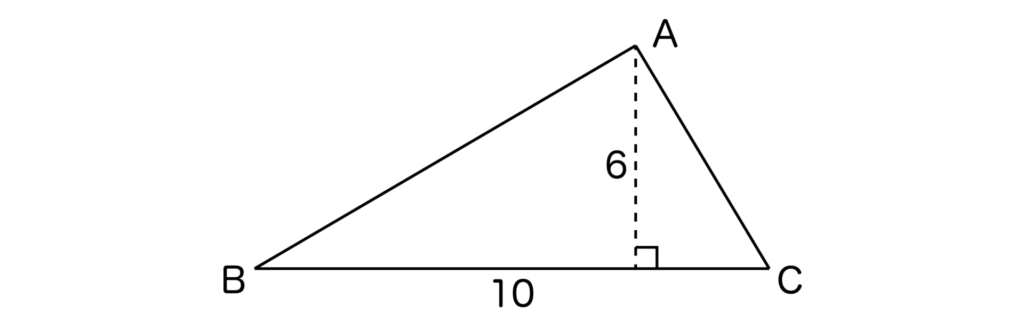
底辺=BC=10、高さ=6なので、三角形ABCの面積=10×6×1/2=30となります。
「底辺×高さ×1/2」は三角形の面積の求め方の公式の定番なので、必ず覚えましょう。
三角形の面積の求め方の公式2つ目
ここからは高校に入ってから学習する内容になります。
以下の三角形ABCの面積Sは、
S=1/2・bcsinA=1/2・casinB=1/2・absinC
で求めることができます。
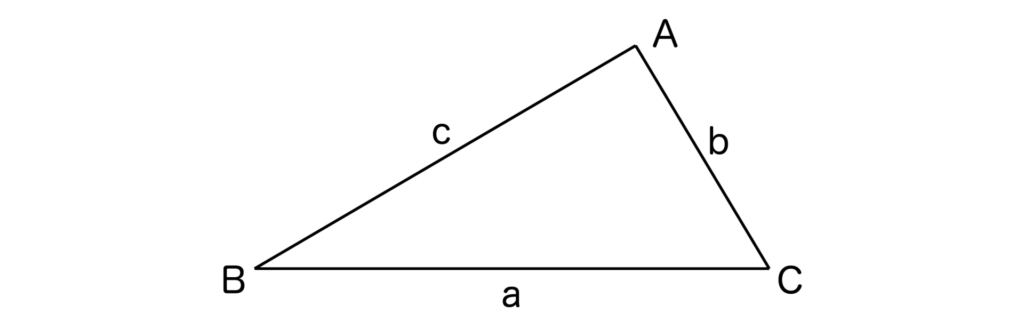
※sinの求め方がわからない人は三角比の覚え方について解説した記事をご覧ください。
では、以上の公式を使って以下の三角形ABCの面積を求めてみましょう。
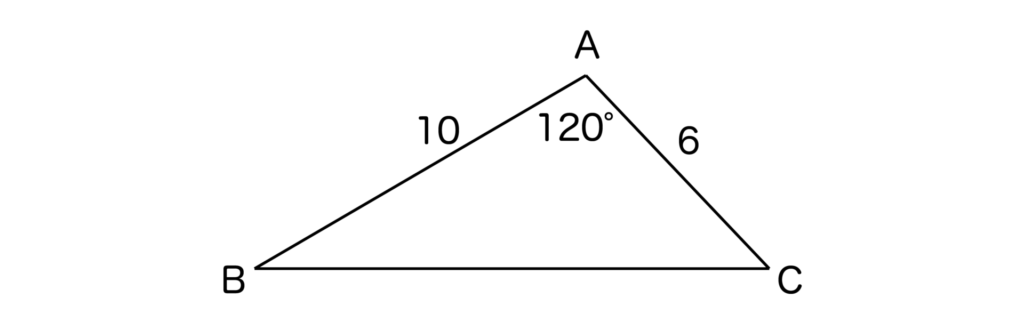
1/2・bcsinAより、1/2・6・10・sin120°=1/2・6・10・√3/2=15√3となります。
※sin120度の求め方について解説した記事もぜひ合わせてご覧ください。
ここからは、S=1/2・bcsinA=1/2・casinB=1/2・absinCが成り立つことを証明していきます。
【証明】
以下の図のように三角形ABCの頂点CからABに垂線CHを下ろします。
[1]∠Aが鋭角のとき、図は以下のようになりますね。
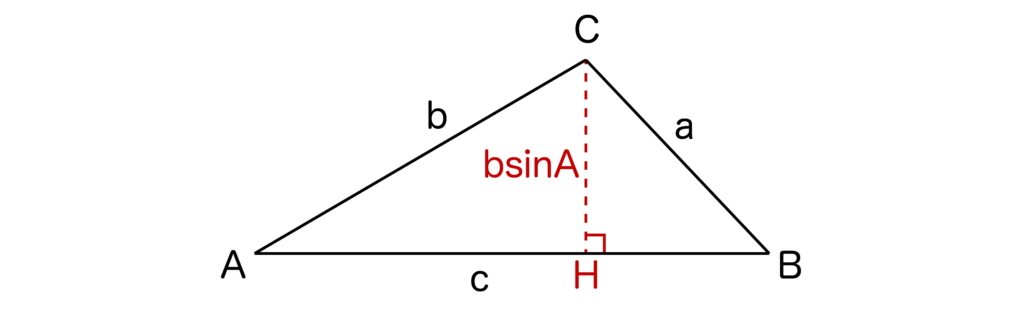
sinA=CH/bより、CH=bsinAとなります。
よって、三角形ABCの面積=c・bsinA・1/2=1/2・bcsinAとなります。
[2]∠A=90°のとき、図は以下のようになりますね。
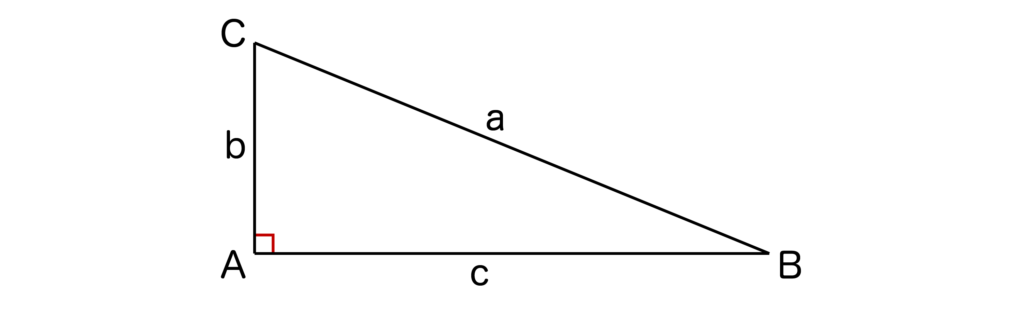
三角形ABCの面積=c・b・1/2=1/2bcとなります。
sinA=sin90°=1なので、1/2・bcsinA=1/2bcとなることがわかります。
[3]∠Aが鈍角のとき、図は以下のようになりますね。
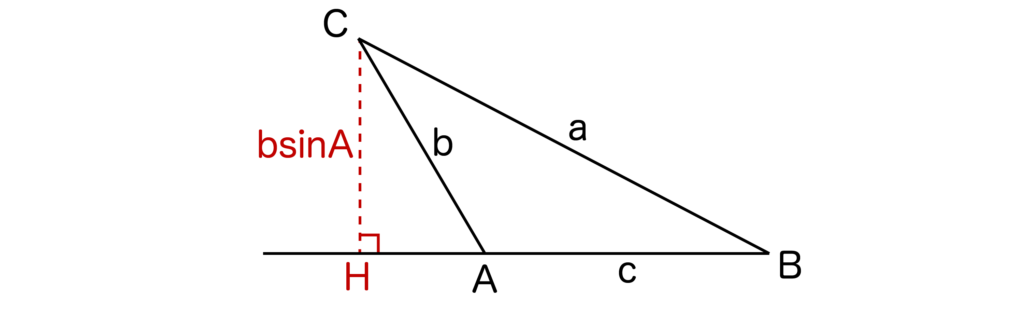
sin∠CAH=CH/bより、CH=bsin∠CAHとなります。
ここで、∠CAH=180°-∠BAC=180°-∠Aより、CH=bsin(180°-∠A)=bsinAとなります。
ゆえに三角形ABCの面積=1/2・c・bsinA=1/2・bcsinAとなります。
残り2つのS=1/2・casinB、S=1/2・absinCに関しても上記と同様に証明が可能です。
S=1/2・bcsinA=1/2・casinB=1/2・absinCは高校数学ではかなり重要な公式の1つなので、必ず覚えておきましょう。
三角形の面積の求め方の公式3つ目(ヘロンの公式)
三角形の面積の求め方の公式3つ目は、
- 以下の図の三角形ABCにおける面積=S
- 2s=a+b+c
とすると、S=√s(s-a)(s-b)(s-c)が成り立ちます。これはヘロンの公式と呼ばれています。

では、例題として以下の三角形ABCの面積をヘロンの公式を使って求めてみましょう。
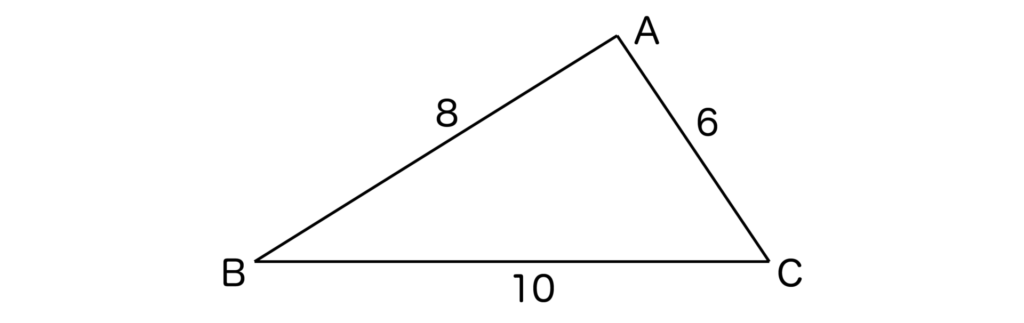
ヘロンの公式より、2s=10+6+8=24となりますね。
したがって、s=12となります。
ゆえに求める三角形ABCの面積=√12(12-10)(12-6)(12-8)=√12・2・6・4=√576=24となります。
ここからは、ヘロンの公式が成り立つ理由を証明していきます。
【証明】
先ほどご紹介した「三角形の面積の求め方の公式2つ目」より、三角形ABCの面積S=1/2・bcsinAが成り立つのでした。
このsinAを3辺の長さa、b、cで表すことを考えましょう。
余弦定理よりcosA=(b2+c2-a2)/2bcですね。
※余弦定理とは何かについて解説した記事もぜひ合わせてご覧ください。
ここで、sin2A+cos2A=1を使います。
※sin2A+cos2A=1が成り立つ理由がわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。
sin2A+cos2A=1より、
sin2A
=1-cos2A
=(1+cosA)(1-cosA)
={1+(b2+c2-a2)/2bc}{1-(b2+c2-a2)/2bc}
=(2bc+b2+c2-a2)/2bc × (2bc-b2-c2+a2)/2bc
={(b+c)2-a2 / 2bc} × {a2-(b-c)2 / 2bc}
={(a+b+c)(-a+b+c)(a-b+c)(a+b-c) / 4b2c2}
ここで、a+b+c=2sとおくと
-a+b+c=2(s-a)、a-b+c=2(s-b)、a+b-c=2(s-c)となりますね。
したがって、sin2A
={2s・2(s-a)・2(s-b)・2(s-c) / 4b2c2}
={4s(s-a)(s-b)(s-c) / (bc)2}
sinA>0であるから、sinA=2√s(s-a)(s-b)(s-c) / bc
これをS=1/2・bcsinAに代入して、ヘロンの公式S=√s(s-a)(s-b)(s-c)が証明できました。
ヘロンの公式は高校数学の教科書では取り上げていない場合もありますが、三角形の面積を求めるためには知っておくとかなり便利なのでぜひ覚えておきましょう。
三角形の面積の求め方の公式4つ目
最後は内接円から三角形の面積を求める方法をご紹介します。
以下のような三角形ABCの面積をS、内接円の半径をrとすると、S=r(a+b+c)/2となります。
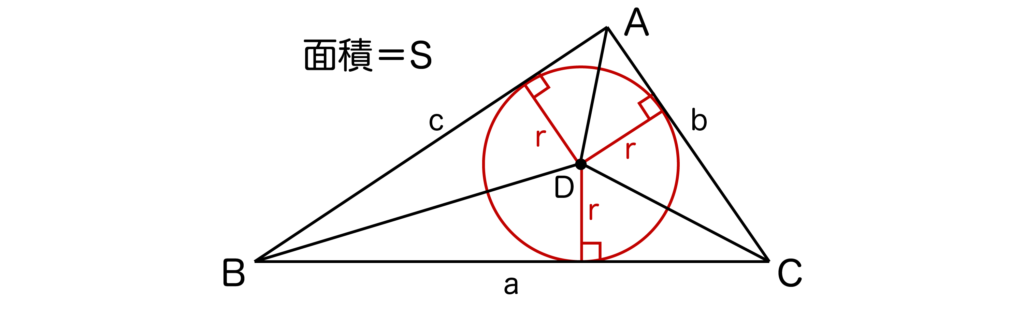
詳しくは内接円とは何かについて解説した記事をご覧ください。
いかがでしたか?
今回は三角形の面積の求め方の公式4つをご紹介していきました。
今回ご紹介した4つの公式はすべて高校数学では暗記必須です。必ず使いこなせるようにしておきましょう。


