皆様は「tan60度の値を求めよ」と言われて即座に求められますでしょうか?
結論としてはtan60度=√3なのですが、中にはこれを暗記している人もいるでしょう。
しかし、これからの三角関数の学習のことを考えると、必ず自力でtan60度の値を求められるようにしておく必要があります。単に暗記するだけでは絶対にこの先の学習でつまずいてしまいます。
そこで今回は早稲田大学教育学部数学科を卒業した筆者がtan60°が√3になる理由3つを図解で丁寧に解説していきます。
tan60°が√3になる理由その1
まずは最も簡単にtan60度を求める方法からご紹介していきます。
以下のように左下に60度がある直角三角形ABCを書いてみましょう。今回は∠BAC=60°となっています。
このとき、三角形ABCの辺の比は1:2:√3となりますね(中学数学で習いましたね)
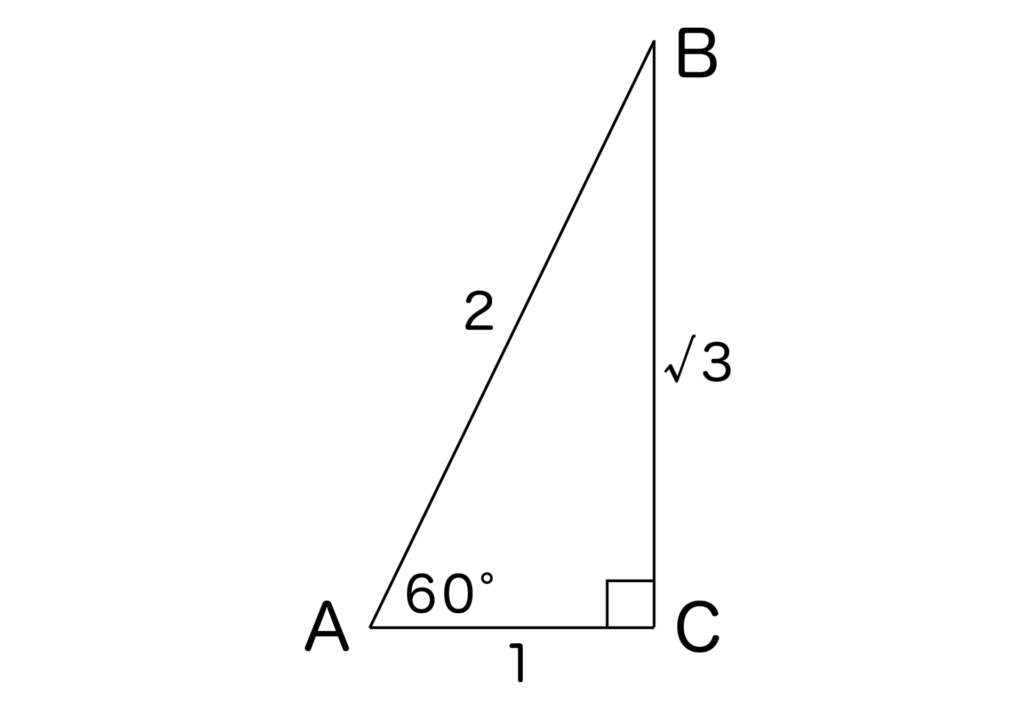
このとき、tan60度=tan∠BAC=BC/ACとなるので、tan60度=√3/1=√3となるのです。
※tan∠BAC=BC/ACとなる理由がわからない人は三角比の覚え方について解説した記事をご覧ください。
以上が最も簡単なtan60度の求め方となります。求めたい角度が90度未満のときは求めたい角度を左下において直角三角形を作るという流れをしっかり理解しておきましょう。
tan60°が√3になる理由その2
以上の図を活用して、少し遠回りな方法ですが別の方法でtan60度を求めてみます。
再び∠BAC=60°の直角三角形を書いてみます。

すると、sin60度=sin∠BAC=BC/AB=√3/2となりますね。
※sin60度、sin-60度の値について詳しく解説した記事もぜひ合わせてご覧ください。
また、cos60度=cos∠BAC=AC/AB=1/2となりますね。
ここで、tanθ=sinθ/cosθでした。
※詳しくは三角比の関係式・相互関係について解説した記事をご覧ください。
つまり、tan60度=sin60度/cos60度=√3/2 ÷ 1/2=√3となります。
先ほど求めたtan60度=tan∠BAC=BC/AC=√3と確かに同じ値になっていますね。
少し遠回りなやり方ではありますが、tanθ=sinθ/cosθは大学入試や共通テストでも頻出なので、公式を覚えるという意味でもこの求め方をご紹介させていただきました。
tan60°が√3になる理由その3
いよいよ最後となるtan60度の求め方をご紹介します。
最後は単位円を使ってtan60度の値を求めてみましょう。単位円とはxy平面において原点Oを中心とした半径=1の円のことでした。
単位円は三角関数の学習を進めるにあたってかなり重要な役割を果たすので、必ず使いこなせるようにしておきましょう。
まずは単位円上に60度を取ってみます(以下の図参照)単位円なのでOP=1となります。
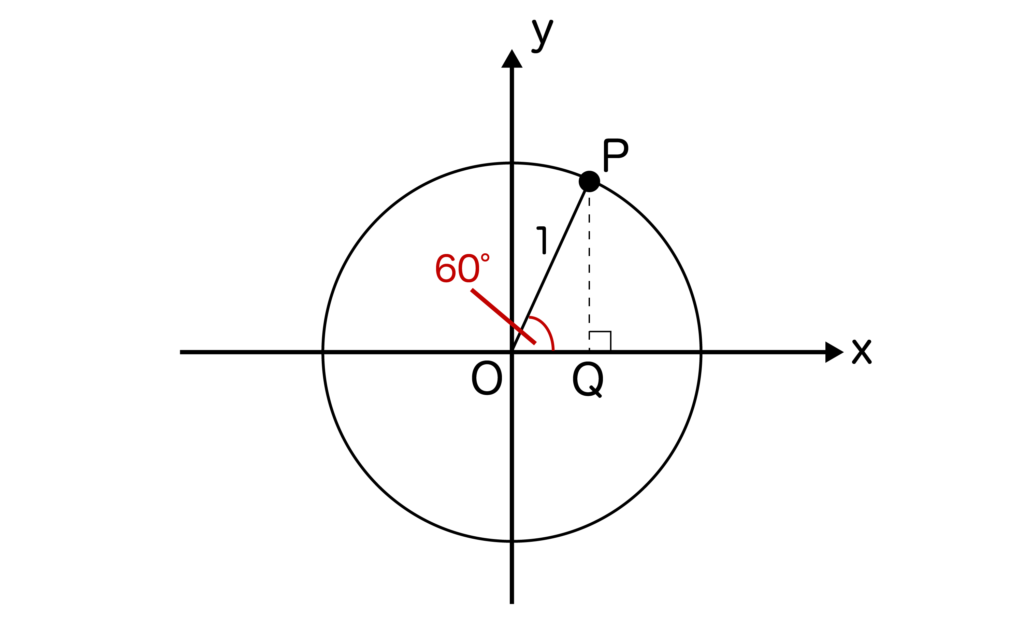
三角形OPQに注目すると、∠POQ=60度、∠OQP=90度なので三角形OPQは辺の比が1:2:√3の直角三角形であることがわかります。
よって、
- OQ=OP×1/2=1×1/2=1/2
- PQ=OP×√3/2=1×√3/2=√3/2
となりますね。
したがって、tan30度=tan∠POQ=PQ/OQ=√3/2 ÷ 1/2=√3となります。
以上が単位円を使ったtan60度の求め方となります。この求め方も必ずできるようにしておきましょう。
tan60度の値を三角比の表で確認しておこう
最後に、tan60度の値を三角比の表で確認しておきましょう。以下の赤枠の部分がtan60度の値になりますね。
※三角比の表の見方がわからない人は三角比の表の見方について解説した記事をご覧ください。
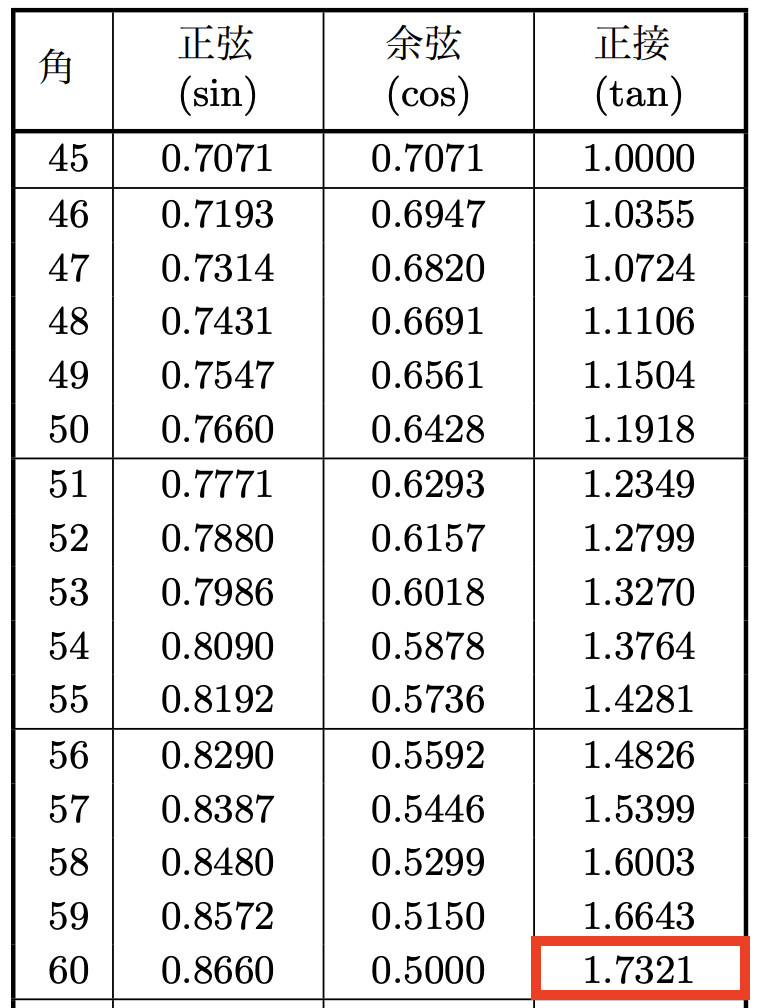
tan60度は小数で1.7321となっています。
√3=1.7320508…(人並みに奢れや)なので、確かに1.7321になっていることが確認できました。
※√3だけでなく√2や√5、√6など様々なルートの近似値の語呂合わせについては平方根とは何かについて解説した記事を参考にしてください。
いかがでしたか?
今回はtan60°が√3になる理由3つを図解で解説していきました。今回ご紹介した3つの求め方はすべて重要です。どの方法でもできるようにしておきましょう。