皆様はsin60度、sin-60度の値を暗記ではなく自力で求めることができますでしょうか?
sin60度、sin-60度の値は暗記しても問題はありませんが「なぜその値になるのか?」をしっかりと理解しておかないとこの先の三角関数の学習で苦戦してしまいます。
そこで今回は早稲田大学教育学部数学科を卒業した筆者がsin60度、sin-60度の値の求め方についてわかりやすく解説していきます。
sin60度の求め方
まずはsin60度の求め方から解説していきます。今回は2通りの方法で求めてみたいと思います。
どちらの方法も使えるようにしておきましょう。
求め方1:60度型の直角三角形を書く
最も簡単な方法となります。
以下のように左下に60度がくるようにして(今回は∠BAC=60度)直角三角形を書いてみましょう。
中学数学で学習した通り、60度型の直角三角形なので辺の比はAC:AB:BC=1:2:√3となります。
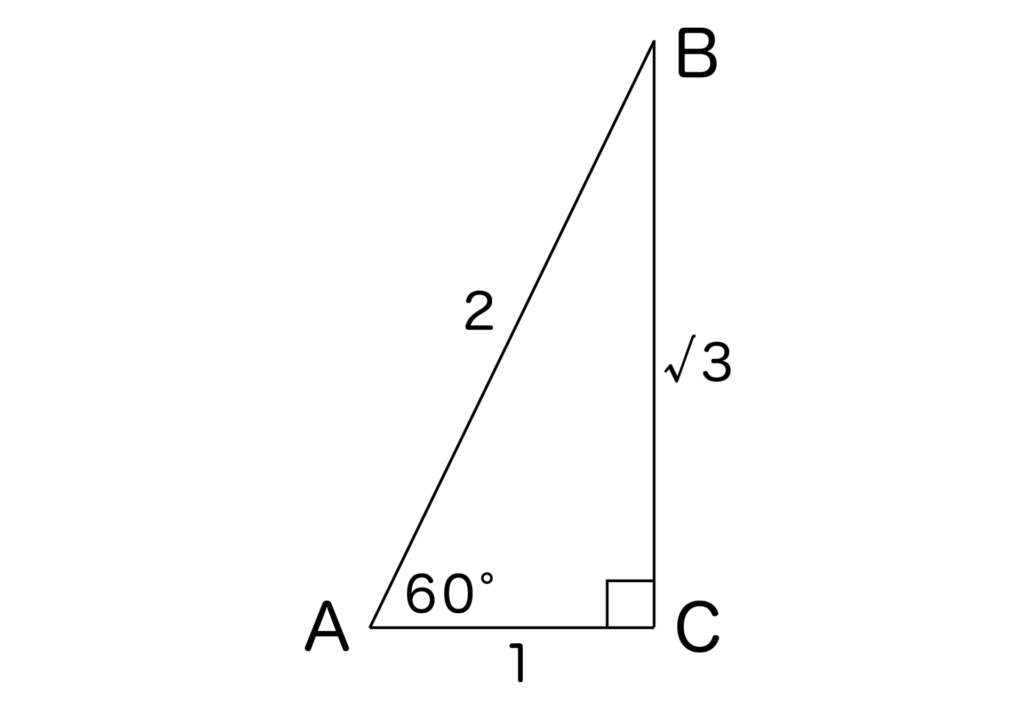
よって、sin60度=BC/AB=√3/2となることがわかります。
sinの求め方がわからない人は三角比の覚え方について解説した記事をご覧ください。
求め方2:単位円の活用
sin60度の求め方2つ目は単位円を活用する方法です。
1つ目にご紹介した方法よりも少し手間がかかってしまいますが、単位円は大学入試でも共通テストでも頻出なので、扱い方を学ぶという意味でも理解しておきましょう。
以下の図のように単位円上で60度を取り、点Pからx軸に対して下ろした垂線とx軸との交点を点Qとします。すると、三角形OPQは60度型の直角三角形となりますね。
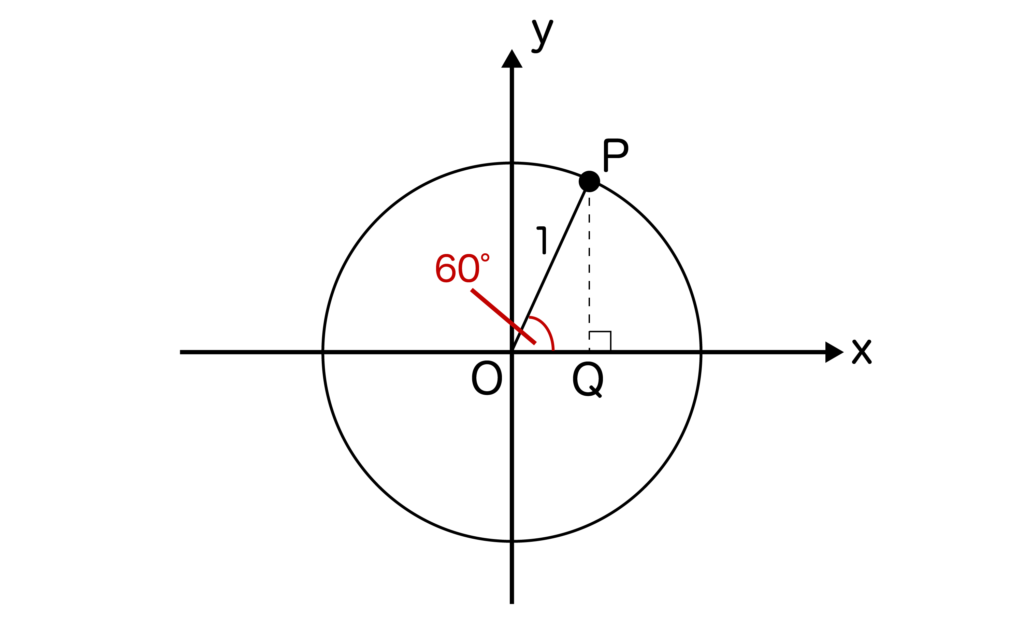
OP:PQ=2:√3であり、単位円なのでOP=半径=1となるので、2:√3=1:PQより、PQ=√3/2となります。
つまり、点Pのy座標=√3/2になるということですね。
単位円においては点P(x、y)を単位円上に取ると、sinθ=y、cosθ=xになるのでした。
※sinθ=y、cosθ=xになる理由がわからない人はsin90度が1なのはなぜかについて解説した記事をご覧ください。
したがって、sin60度=点Pのy座標=√3/2となります。
先ほどご紹介した「求め方1」にて自分で60度型の直角三角形を書いたときと同じ値になりましたね。
単位円を使ってsin30度の求め方について解説した記事やsin45度の求め方について解説した記事もご用意しているので、単位円についてもっと学習したい人はぜひ参考にしてください。
sin-60度の求め方
では、sin-60度はどうやって求めれば良いでしょうか?
今回は角度が-60度で負の数になっているので、先ほどご紹介した「求め方1」のように自力で直角三角形を書くのは難しそうですね。
なので、単位円で考えてみましょう。単位円上に-60度を取ると以下のようになりますね。
※単位円においては以下の図でいうところのQOを0度とし、反時計回りが+(プラス)、時計回りが-(マイナス)となります。よって、-60度はQOから時計回りに60度進んだ箇所になります。
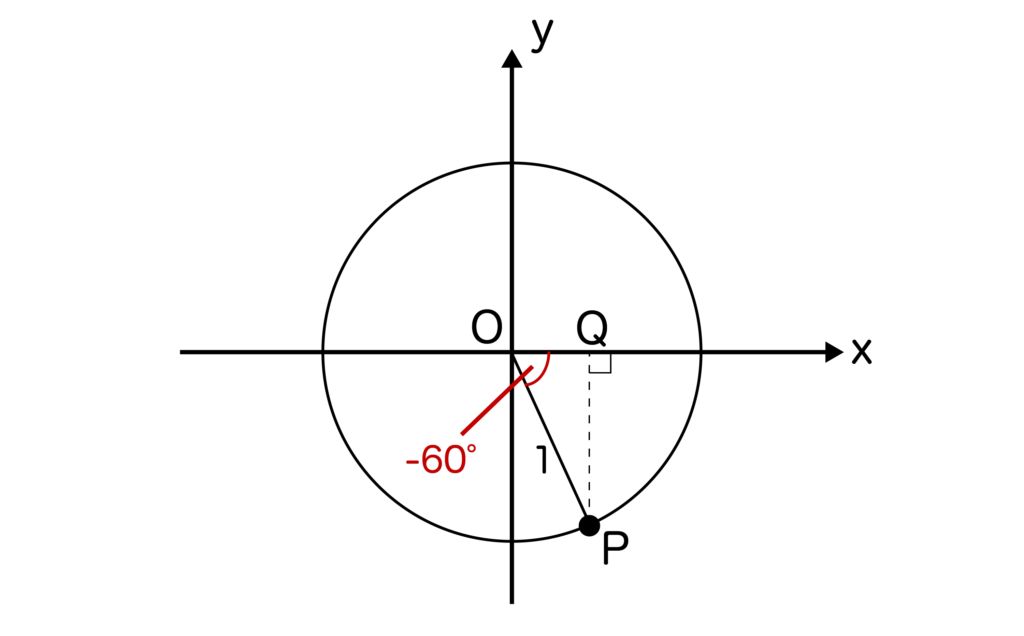
ここで、先ほどと同様にPQの長さを求めましょう。OP:PQ=2:√3で、OP=1なので2:√3=1:PQよりPQ=√3/2となります。
ここで注意すべきはPQ=√3/2より、点Pのy座標は-√3/2となることです。
上記でも解説した通り、単位円においては点P(x、y)を単位円上に取ると、sinθ=y、cosθ=xになるのでした。
したがって、sin-60度=点Pのy座標=-√3/2となります。マイナスが付くことに十分注意してください。
以上がsin-60度の求め方となります。単位円はマイナスの角度の三角比を求めるときに役に立つので、必ず扱えるようにしておきましょう。
【おまけ】cos±60度、tan±60度も求めてみよう!
以上でsin60度とsin-60度は求めることができましたが、おまけとしてcos60度、cos-60度、tan60度、tan-60度も求めてみましょう。
cos60度、tan60度
cos60度・tan60度は自分で60度型の直角三角形を書いて求めるのが手っ取り早そうですね。
先ほどと同じように∠BAC=60度の直角三角形を書いてみます。

したがって、cos60度=AC/AB=1/2、tan60度=BC/AC=√3となります。
※tan60°が√3になる理由3つについて解説した記事もぜひ合わせてご覧ください。
cos-60度、tan-60度
今回は角度がマイナスの値なので単位円で考えます。先ほどと同様に単位円上に-60度を取りましょう。

OP:OQ=2:1で、OP=1より、2:1=1:OQとなるので、OQ=1/2となります。
つまり、点Qのx座標=1/2です。
単位円においては点P(x、y)を単位円上に取ると、sinθ=y、cosθ=xです。
点Pのx座標は点Qのx座標と等しいので、cos-60度=1/2となります。
また、tan-60度=sin-60度/cos-60度なので、-√3/2 ÷ 1/2=-√3となります。
※tan-60度=sin-60度/cos-60度がわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。
いかがでしたか?
今回はsin60度、sin-60度の値の求め方について解説しました。特にマイナスの角度の三角比の求め方は苦戦する人が多いので、ぜひ単位円を使えるように訓練を積みましょう。