三角比の覚え方！角度や公式・定義、求め方も図でわかりやすく紹介！

数学1では三角比（sin・cos・tan）が新たに登場しますが、三角比で苦戦する高校生は非常に多いです。

三角比の分野では三角比の定義や公式など基本をしっかりと抑えておかなくてはこの先も間違いなく苦戦してしまいます。

そこで今回は早稲田大学教育学部数学科を卒業した筆者が三角比の覚え方や角度や公式・定義、求め方や覚え方などを図でわかりやすく紹介していきます。

この先、三角比でつまずかないためにも、ぜひ最後までご覧いただき、内容をしっかり理解してください。

三角比（sin・cos・tan）の定義

まずは三角比（sin・cos・tan）の定義から解説します。

以下の図のように、∠POQが鋭角である直角三角形OPQを考えます。

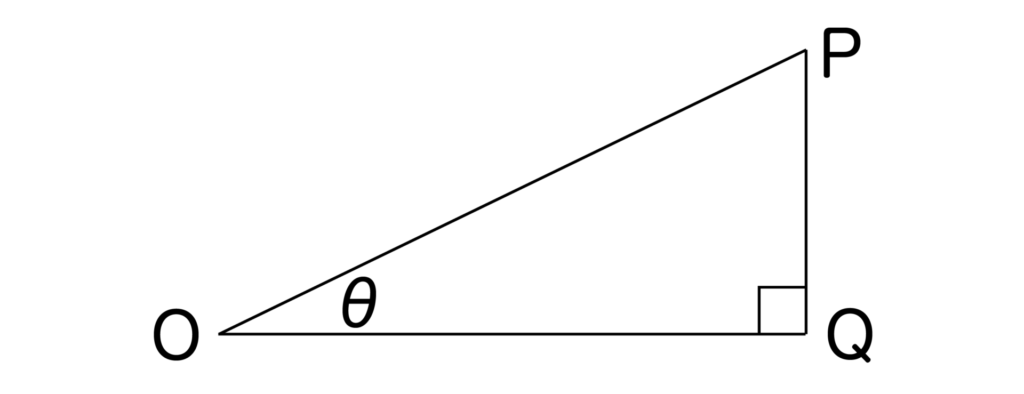
∠POQの大きさをθ（シータと読む）とすると、

• sinθ＝PQ/OP
• cosθ＝OQ/OP
• tanθ＝PQ/OQ

となります。

ちなみに、sinはsineの略で「サイン」と読みます。日本語では正弦とも言われます。

cosはcosineの略で「コサイン」と読みます。日本語では余弦とも言われます。

tanはtangentの略で「タンジェント」と読みます。日本語では正接とも言われます。

以上が三角比（sin・cos・tan）の定義となります。基本事項として必ず覚えておきましょう。

三角比（sin・cos・tan）の例

以上を踏まえて、三角比の例を見ていきましょう。

例えば、∠BAC＝30°の直角三角形ABCのsin・cos・tanを求めてみましょう。

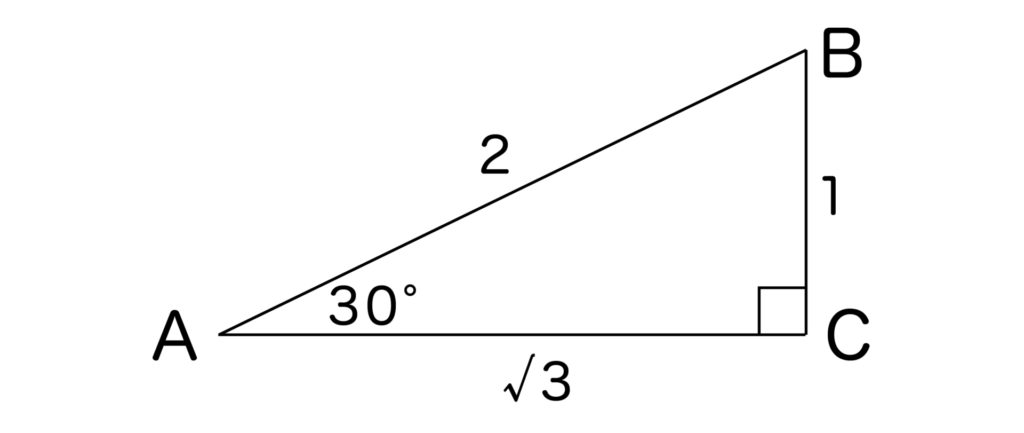
sin30°＝BC/AB＝1/2となります。

cos30°＝AC/AB＝√3/2となります。

tan30°＝BC/AC＝1/√3となります。

※単位円を使ってsin30度が1/2になる理由について解説した記事もぜひ合わせてご覧ください。

では、60°の場合はどうなるでしょうか？以下のような直角三角形を書いて考えてみましょう。

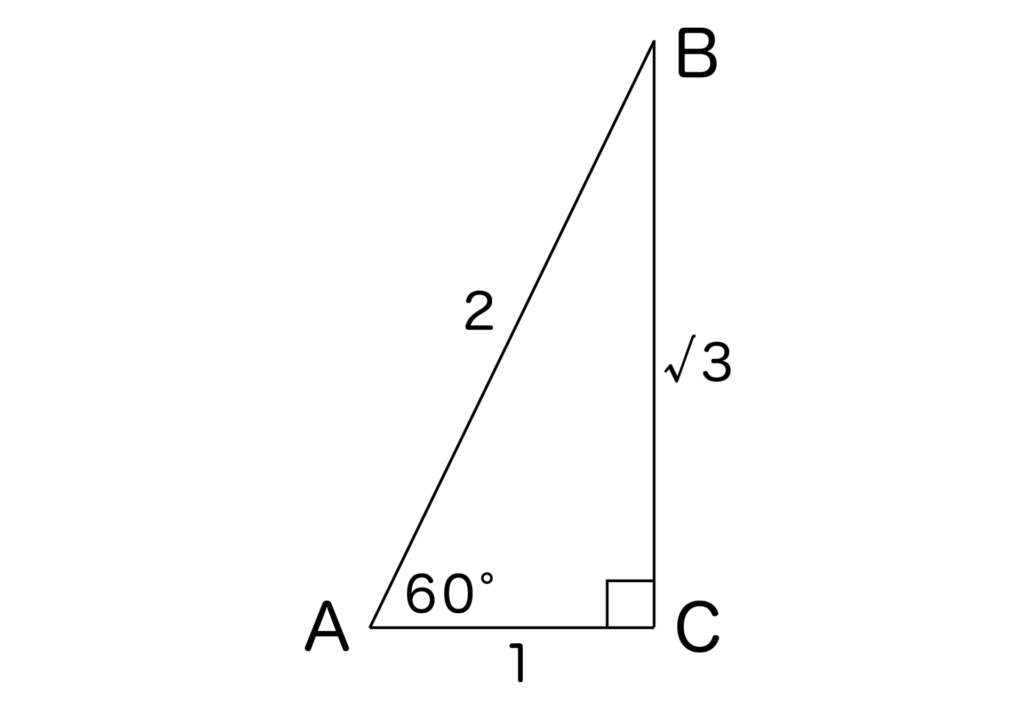
すると、30°のときと同様に考えて、

sin60°＝√3/2

cos60°＝1/2

tan60°＝√3

が求まりますね。

※sin60度、sin-60度の値の求め方について詳しく解説した記事や※tan60°が√3になる理由3つについて解説した記事もぜひ合わせてご覧ください。

三角比（sin・cos・tan）を考えるときは左下に求めたい角度を用意した直角三角形で考えるのが定石ですので、必ず覚えておきましょう。

三角比（sin・cos・tan）の覚え方

三角比学習したばかりだと、三角比（sin・cos・tan）の定義を覚えるのに苦戦する人もいます。

そんな人のために、三角比（sin・cos・tan）の覚え方をご紹介します。

まずcosからご紹介します。cosは以下の図のように角度に対して「C」を書くように覚えましょう。

斜辺が分母で底辺が分子となります。

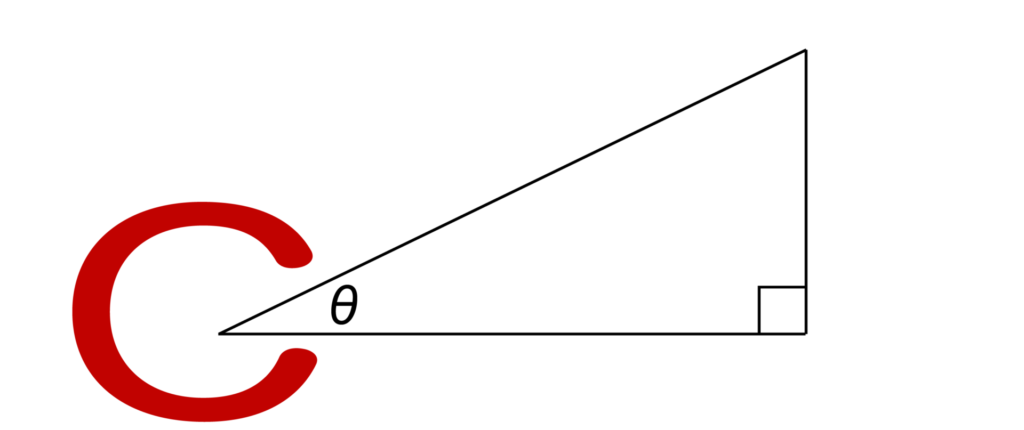
これは非常に覚えやすくて有名な覚え方なので、ぜひ「Cを書く」で覚えて頂ければと思います。

続いてsinですが、これはcosがわかっていれば問題なく求めることができるかと思います。

sinもcosも分母は斜辺で、cosは分子が底辺なのでsinの分子は自動的に残った辺（高さ）になります。

残りのtanですが、これも覚えやすい覚え方があります。先ほどcosでは「C」を書きましたが、tanでは「筆記体のt」を書きます。

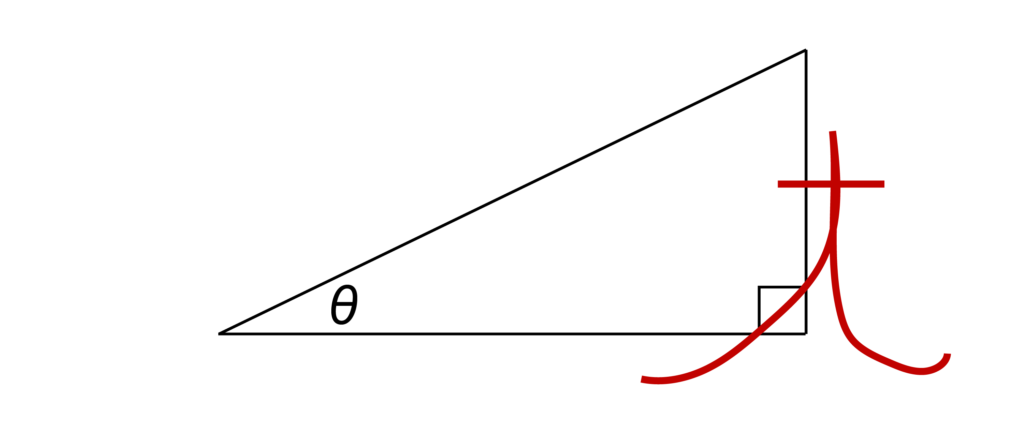
conと同様に書き始めは分母なので、tanは底辺が分母になって高さが分子になります。

sin・cos・tanは必ず覚えておかなくてはなりません。ぜひトイレの壁などに貼って覚えてみてください。

三角比（sin・cos・tan）の特徴

三角比（sin・cos・tan）は1つの鋭角の大きさが決まると、辺の長さがいくつであっても三角比（sin・cos・tan）の値は変わりません。

例えば、辺の長さが以下のような直角三角形を比べてみましょう。両方とも∠BAC=30°です。

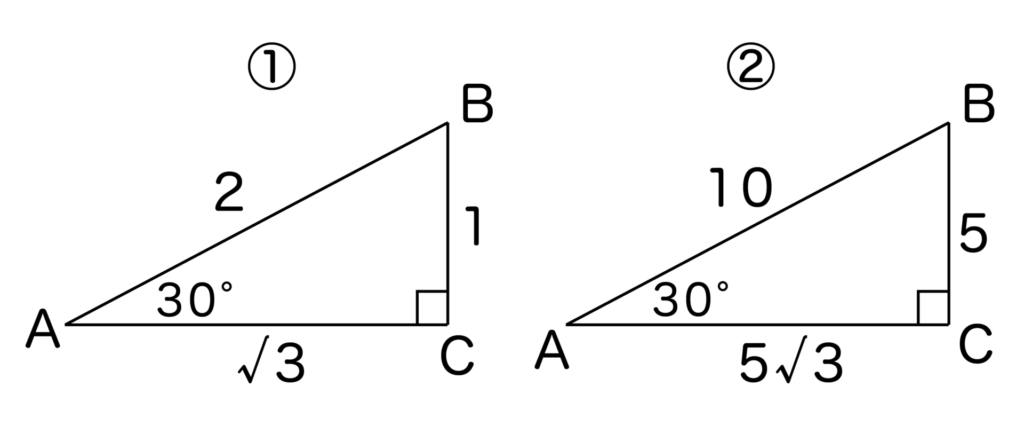
①の直角三角形では、

• sin30°＝1/2
• cos30°＝√3/2
• tan30°＝1/√3

となりますね。

②の直角三角形でも、

• sin30°＝5/10＝1/2
• cos30°＝5√3/10＝√3/2
• tan30°＝5/5√3＝1/√3

となるので、結果的に①と同じになっていることがわかります。

なので、三角比（sin・cos・tan）を求めるときは辺の長さではなく、辺の比で考えることをおすすめします。

例えば、∠BAC＝30°の直角三角形の辺の比は1：2：√3であることを中学数学で習いましたね。

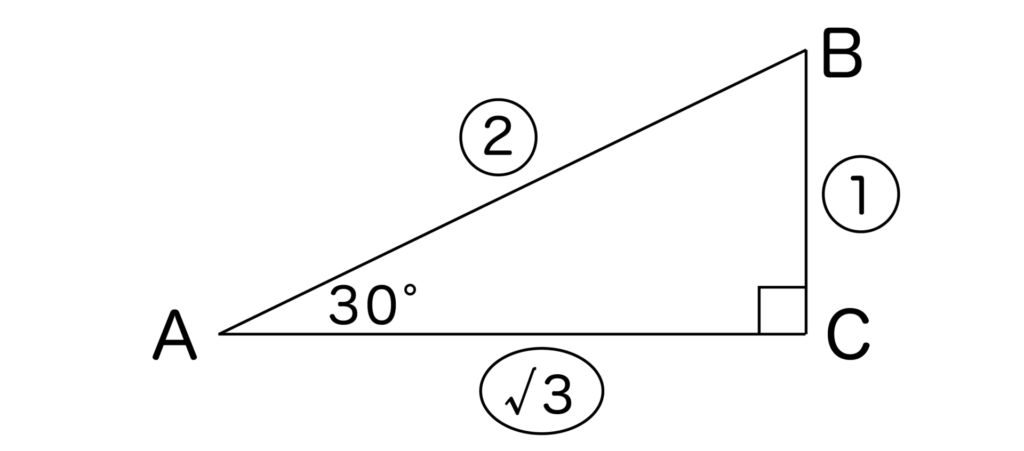
この1：2：√3をもとにして三角比（sin・cos・tan）を考えると余計や計算（約分）をする手間が省けます。

三角比（sin・cos・tan）の公式

ここからは三角比（sin・cos・tan）の公式を2つご紹介していきます。

※本記事では公式のご紹介のみとなります。公式の証明は三角比の関係式・相互関係について解説した記事をご覧ください。

公式その1：三角比の相互関係

θが鋭角、すなわち0°<θ<90°のとき

• tanθ＝sinθ/cosθ
• sin²θ+cos²θ＝1
• 1+tan²θ＝1/cos²θ

が成り立ちます。

※sinθの2乗は（sinθ）²ではなく、sin²θと記載し「サイン2乗θ」と読みます。con、tanに関しても同様です。

特に、2つ目のsin²θ+cos²θ=1は大学入試・共通テストで頻出ですので、必ず覚えておいてください。

公式その2：90°-θの三角比

θが鋭角、すなわち0°<θ<90°のとき

• sin（90°-θ）＝cosθ
• cos（90°-θ）＝sinθ
• tan（90°-θ）＝1/tanθ

が成り立ちます。

有名な角度の三角比（sin・cos・tan）を求めてみよう

最後に、以上で解説したことを頭に入れて有名な角度の三角比（sin・cos・tan）を求めてみましょう。

30°と60°のパターンは先ほど解説したので、ここからは45°を考えてみましょう。

45°の三角比

まずは以下のように45°の直角三角形を書きましょう。45°の直角三角形の辺の比は1：1：√2でしたね。

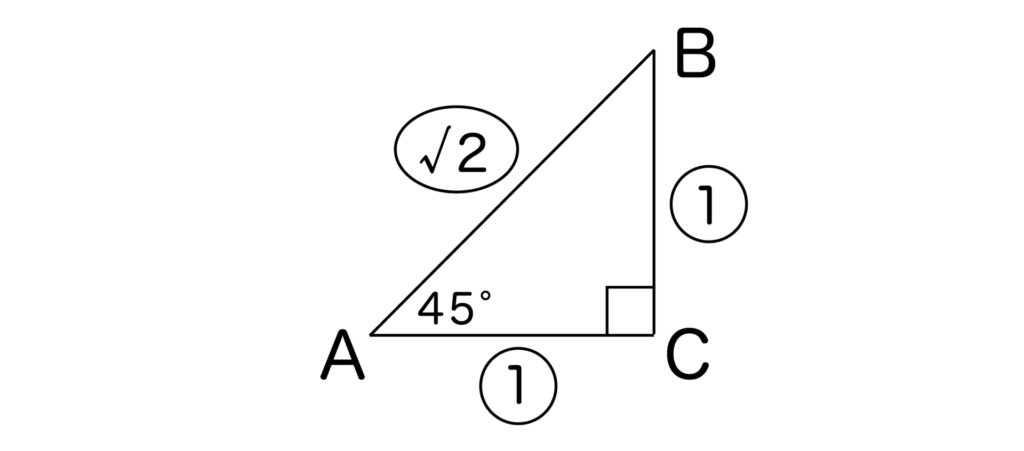
よって、

• sin45°＝1/√2
• cos45°＝1/√2
• tan45°＝1

となります。

※単位円を使って45度の三角比求める方法について解説した記事もご用意しているので、ぜひ合わせてご覧ください。

本記事でご紹介した30°、45°、60°の三角比（sin・cos・tan）は大学入試や共通テストで必ずと言って良いほど使うので、暗記しても問題はありません。

しかし、ただ単に暗記するのではなく「なぜsin・cos・tanがその値になるのか？」をしっかりと理解してください。

※ちなみにですが、sin90度＝1となります。sin90度が1なのはなぜかについて解説した記事もぜひ参考にしてください。

三角比（sin・cos・tan）の練習問題

最後に三角比（sin・cos・tan）の練習問題をご用意しました。

三角比（sin・cos・tan）はとにかくたくさんの問題を解いて慣れることが重要です。ぜひチャレンジしてみてください。

【練習問題】

以下の図において、sinθ、cosθ、tanθの値を求めなさい。

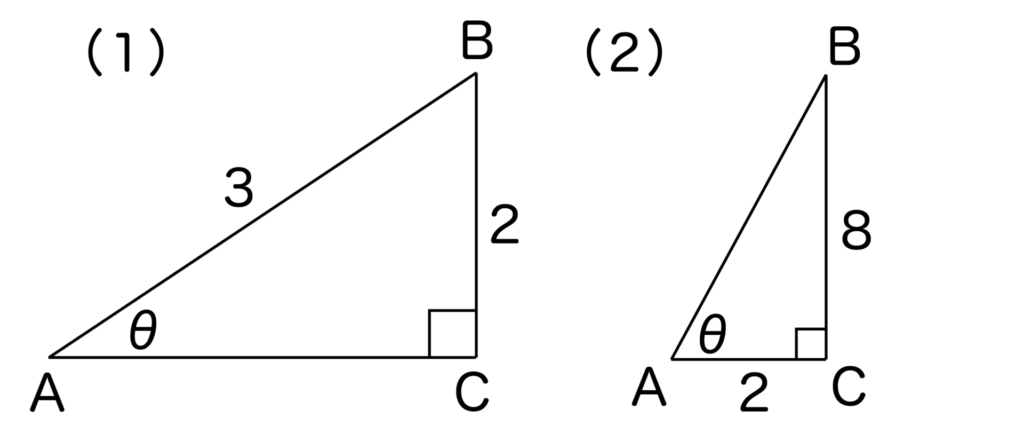
【解答＆解説】

（1）三平方の定理より、AC＝√32-22＝√5となります。

よって、

sinθ＝BC/AB＝2/3

cosθ＝AC/AB＝√5/3

tanθ＝BC/AC＝2/√5

となります。

（2）三平方の定理より、AB＝√82+22＝√68＝2√17となります。

よって、

sinθ＝BC/AB＝8/2√17＝4√17/17

cosθ＝AC/AB＝2/2√17＝1/√17

※1/√17は分母の有利化を行って√17/17としても問題ありませんが、1/√17も綺麗な形なので有利化を行わなくても問題ありません。

tanθ＝BC/AC＝8/2＝4

となります。

いかがでしたか？今回は三角比の基本事項（定義や公式、覚え方など）について解説していきました。

冒頭でも解説した通り、本記事の内容をしっかり理解しておかなけば、この先の三角比の学習で必ずつまずいてしまいます。

ぜひ何度も本記事を見返して、三角比（sin・cos・tan）を求められるようにしておきましょう。