二次不等式を解くにあたり、場合分けが必要なケースがあります。
しかし、場合分けはどういった条件で場合分けをすればいいか悩んでしまう人も多いのではないでしょうか?
そこで今回は早稲田大学教育学部数学科を卒業した筆者が二次不等式の場合分けについて例題を使いながら解説していきます。
ぜひ最後まで読んで、二次不等式の場合分けの感覚を掴んでいきましょう。
二次不等式の場合分けその1
二次不等式の場合分けに慣れるにはたくさんの問題を解くことが重要です。
なので、まずは例題を見ていきましょう。
【例題】
二次不等式x2+(2-a)x-2a≦0を解きなさい。ただし、aは定数とする。
【解答&解説】
二次不等式の解き方を解説した記事をご覧いただくとわかりますが、二次不等式を解くときはまずは因数分解できるかを確認するのでした。
x2+(2-a)x-2aを因数分解すると(x+2)(x-a)となりますね。
※数学1の因数分解について解説した記事もご用意しているので、ぜひ参考にしてください。
つまり、x2+(2-a)x-2a≦0は(x+2)(x-a)≦0となります。
よってx=-2、αとなるわけですが、x=-2のときは(x+2)(x-a)=(x+2)2となるので重解になりますね。
なので、a=-2を境として場合分けを行いましょう。
[1]a<-2のとき、解はa≦x≦-2となります。
[2]a=-2のとき、(x+2)2≦0となるので、解はx=-2となります。
※解がx=-2となる理由がわからない人は二次不等式の解5パターンについて解説した記事をご覧ください。
[3]-2<aのとき、解は-2≦x≦aとなります。
二次不等式の場合分けその2
では、2つ目の例題です。
【例題】
不等式ax2≦axを解きなさい。
【解答&解説】
問題文が「二次不等式」ではなく「不等式」となっていることに注意してください。
つまり、a=0の可能性もあり得ます。
ax2≦axからax(x-1)≦0・・・①となりますね。
[1]a>0のとき、x(x-1)≦0となるので解は0≦x≦1となります。
[2]a=0のとき、①は0・x(x-1)≦0となるので、xがどんな値でも成り立ちます。よって解はすべての実数となります。
※すべての実数の意味がわからない人は、二次不等式の全ての実数とは何かについて解説した記事をご覧ください。
[3]a<0のとき、x(x-1)≧0となるので解はx≦0、1≦xとなります。
二次不等式の場合分けその3
例題3つ目となります。こちらも問題文に注意して解いていきましょう。
【例題】
任意の実数xに対して、不等式ax2-2√3x+a+2≦0が成り立つような定数aの範囲を求めなさい。
※実数の意味がわからない人は実数とは何かについて解説した記事をご覧ください。
【解答&解説】
今回も問題文が「二次不等式」ではなく「不等式」となっていることに注意してください。
つまり、a=0のときとa≠0で場合分けが必要です。
[1]a=0のとき、不等式は-2√3x+2≦0となり、例えばx=0のとき不等式は成り立たちません。
[2]a≠0のとき、y=ax2-2√3x+a+2とすると、yは二次関数のグラフになりますね。
問題文の通り、任意の実数xつまり全ての実数xに対してax2-2√3x+a+2≦0つまりy≦0が成り立つためには、yが以下のようなグラフになれば良いですね。
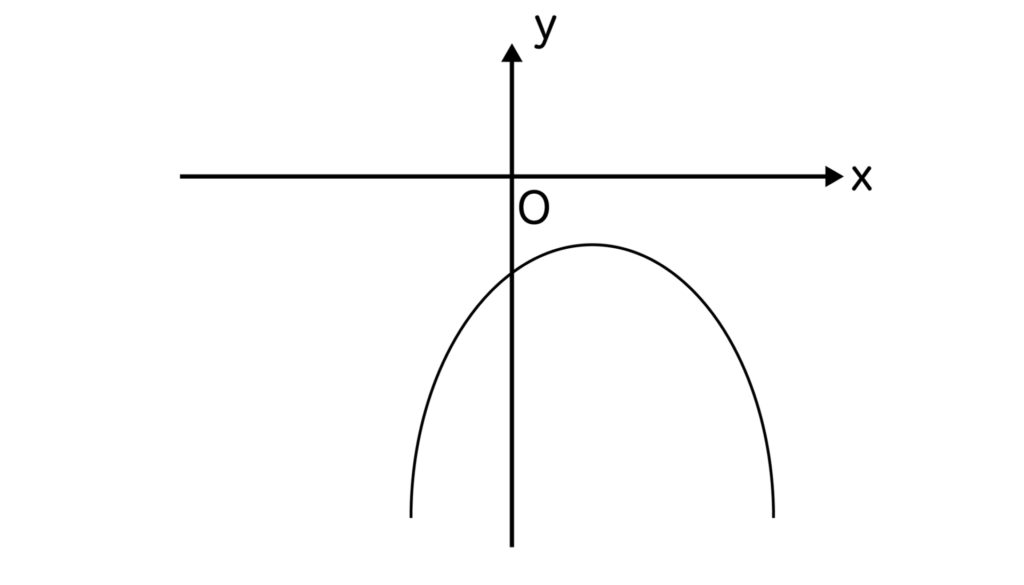
つまり、a<0かつ判別式D≦0になれば良いということがわかります(y≦0なので、判別式D=0でも問題ありません)
※判別式がわからない人は二次方程式の判別式とは何かについて解説した記事をご覧ください。
判別式D=(-√3)2-a(a+2)=-a2-2a+3=-(a+3)(a-1)となるので、D≦0よりa≦-3、1≦aが求まります。
最後にa<0との共通範囲を考えます。
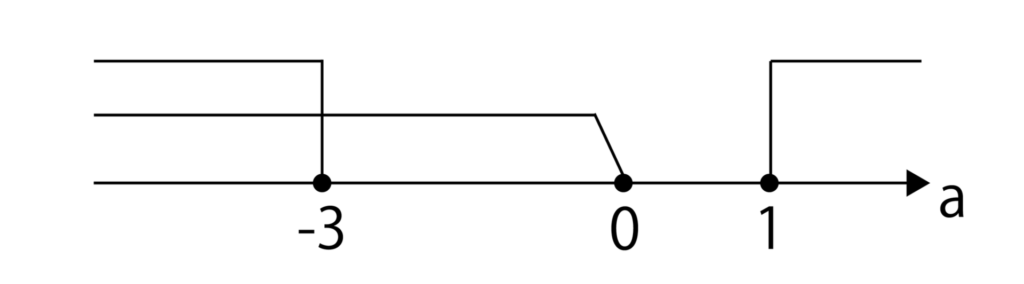
※共通範囲の考え方がわからない人は一次不等式とは何かについて解説した記事をご覧ください。
よって答えはa≦-3・・・(答)となります。
二次不等式の場合分けその4
二次不等式に絶対値が含まれる場合も場合分けが必要なケースが多いです。
【例題】
不等式|x2-2x-3|≧3-xを解きなさい。
【解答&解説】
x2-2x-3を因数分解すると(x+1)(x-3)となりますね。
- x2-2x-3≧0の解はx≦-1、3≦x
- x2-2x-3<0の解は-1<x<3
ですね。
[1]x≦-1、3≦xのとき、不等式はx2-2x-3≧3-xとなるのでx2-x-6≧0より、x≦-2、3≦x・・・①となります。
これはx≦-1、3≦xを満たしています。
[2]-1<x<3のとき、不等式は-(x2-2x-3)≧3-xとなるのでx2-3x≦0となるので、0≦x≦3となります。
-1<x<3との共通範囲は以下の通り0≦x<3・・・②となります。
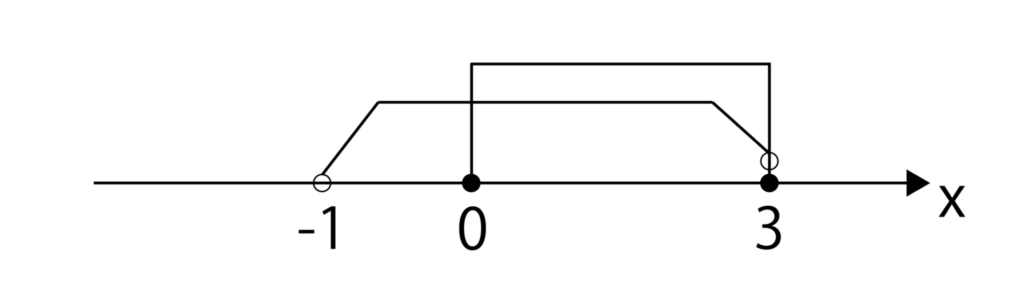
よって答えは①と②を合わせた範囲でx≦-2、0≦x・・・(答)となります。
二次不等式の場合分けその5
いよいよ最後の例題となります。
【例題】
二次不等式x2+2mx+1≧0が、0≦x≦2において常に成り立つように定数mの範囲を定めよ。
【解答&解説】
y=x2+2mx+1とします。
まずはy=x2+2mx+1の頂点の軸を求めましょう。
x2+2mx+1=(x+m)2-m2+1となるので、y=x2+2mx+1は下に凸のグラフで軸はx=-mとなりますね。
※二次関数の頂点・軸の求め方について解説した記事もぜひ参考にしてください。
ここからは、軸x=-mが0≦x≦2にあるかどうかで場合分けを行っていきます。
[1]-m<0つまり、m>0のとき
0≦x≦2においてyはx=0で最小値=1を取ります。
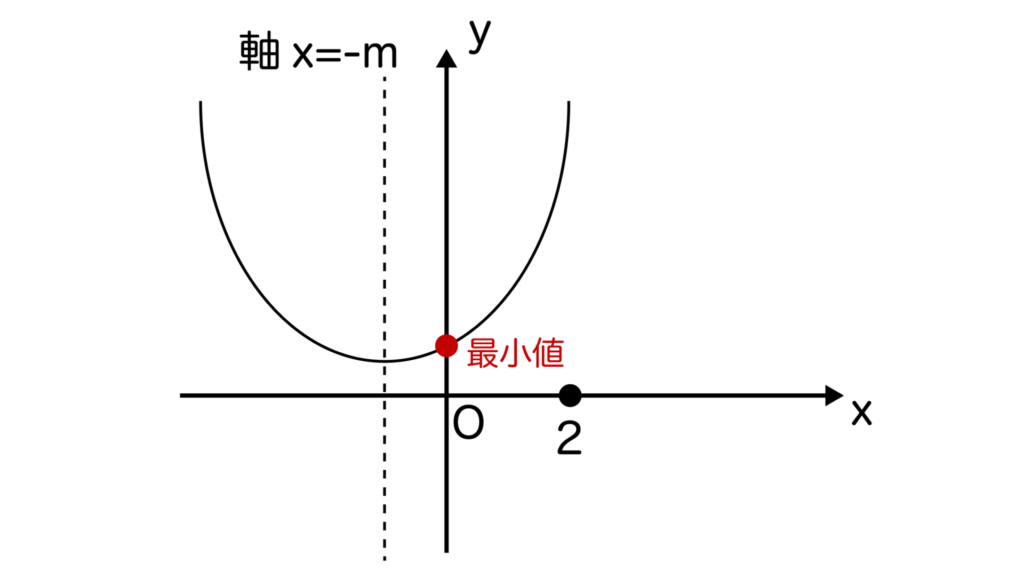
よって、m>0のときは0≦x≦2において常にy≧0が成り立つことがわかります。
[2]0≦-m≦2つまり、-2≦m≦0のとき
0≦x≦2においてyはx=-mで最小値-m2+1を取ります。
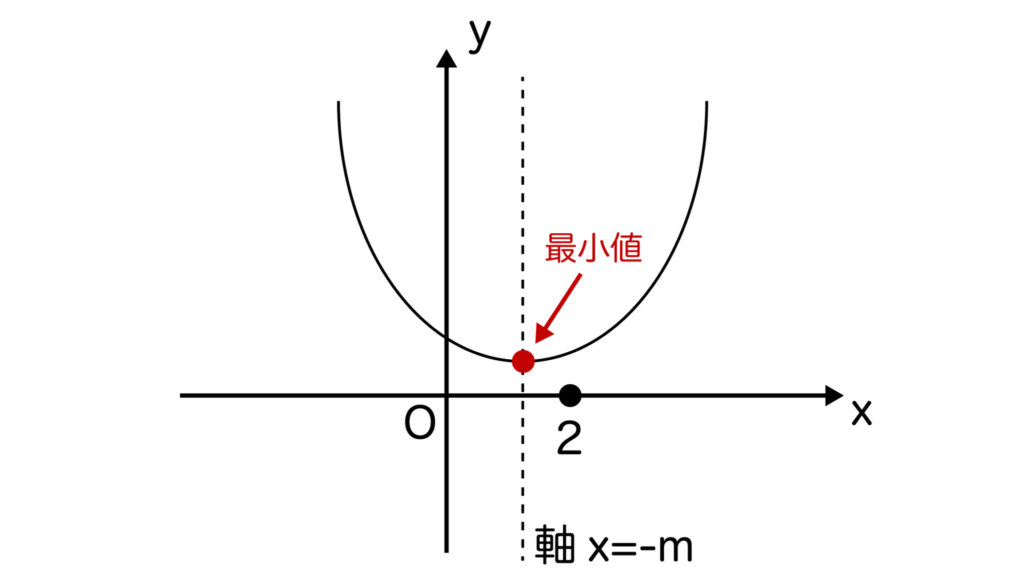
よって、0≦x≦2において常にy≧0が成り立つための条件は-m2+1≧0
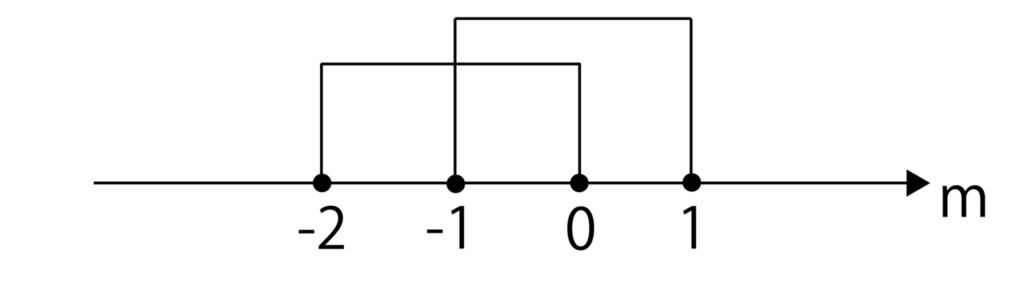
すなわち、(m+1)(m-1)≦0より-1≦m≦1となります。
-2≦m≦0との共通範囲は以下より、-1≦m≦0となります。
[3]2<-mつまり、m<-2のとき
0≦x≦2においてyはx=2で最小値=22+2m・2+1=5+4mを取ります。
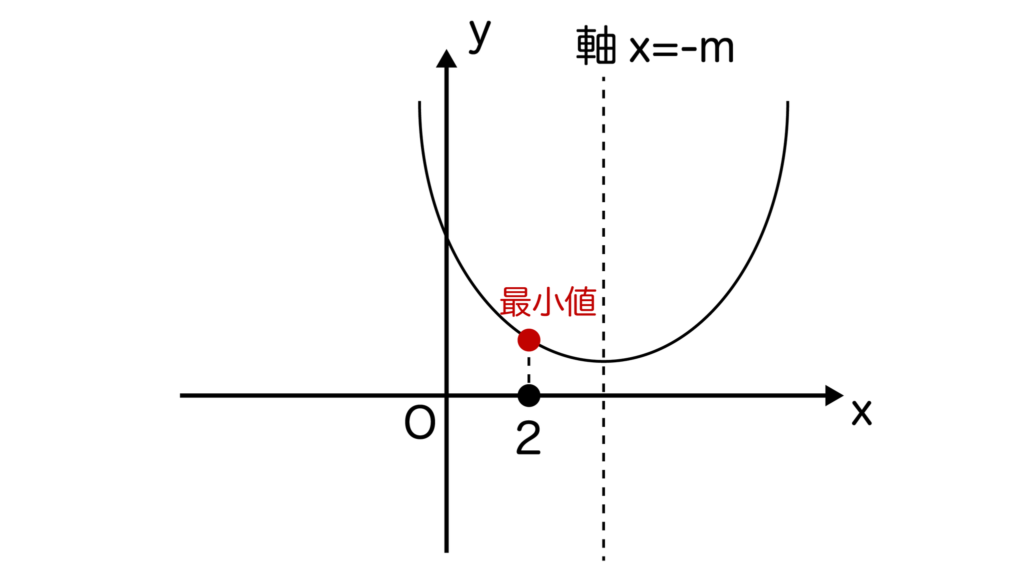
よって、0≦x≦2において常にy≧0が成り立つための条件は5+4m≧0
すなわち、m≧-5/4となりますが、これとm<-2の共通範囲はありません。
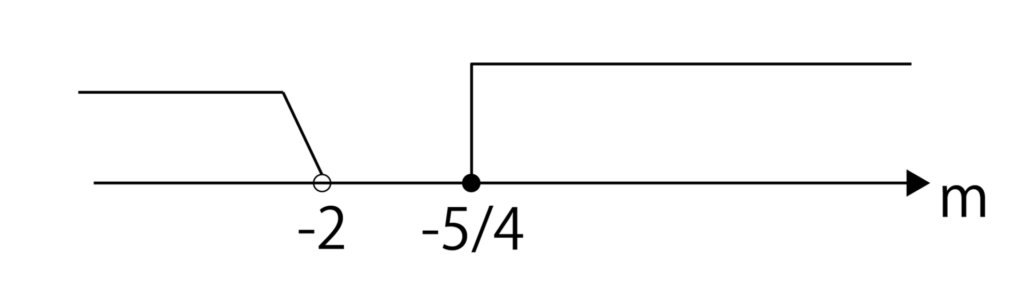
よって、[1]〜[3]より、m≧1・・・(答)となります。
いかがでしたでしょうか?
今回は二次不等式の場合分けについて例題で解説していきました。場合分けは最初は慣れないかと思いますが、問題をたくさん解いていくにつれて感覚が養われていきます。
ぜひたくさんの問題を解いて場合分けに慣れていってください。


