二次不等式では解=解なしとなるケースが4つあります。
しかし、なぜ解なしになるのかをしっかり理解できている人は少ないのではないでしょうか?
そこで今回は早稲田大学教育学部数学科を卒業した筆者が二次不等式において解なしとなる4つのケースを全てご紹介し、なぜ解なしになるのかを解説していきます。
※二次不等式の解き方について解説した記事もぜひ参考にしてください。
解なしとはどういう状況?
まずは解なしとはどういう状況なのかについて解説します。
例えばxを正の数としたとき「4x=-20になるxを求めよ」と言われたら困りますね。
x=-5は正の数ではないので不適となります。つまり、この場合は4x=-20を満たすxは1つも存在しないということになります。
このように、方程式において条件を満たす数が1つも存在しない状況のことを「解なし」と言います。
二次不等式で解なしになる4つのケース
二次不等式では解なしになるケースは以下の4つです。
a>0かつ判別式D=0のとき、二次方程式ax2+bx+c=0の重解=αとすると、
- ax2+bx+c<0の解=解なし
- (x-α)2<0の解=解なし
a>0かつD<0のとき、
- ax2+bx+c<0の解=解なし
- ax2+bx+c≦0の解=解なし
それぞれ順番に詳しくみていきましょう。
ax^2+bx+c<0の解=解なし
a>0かつ判別式D=0で、二次方程式ax2+bx+c=0の重解=αとのことです。
※判別式がわからない人は判別式とは何かについて解説した記事をご覧ください。
以上をもとにして二次関数y=ax2+bx+cのグラフを書いてみると以下のようになりますね。
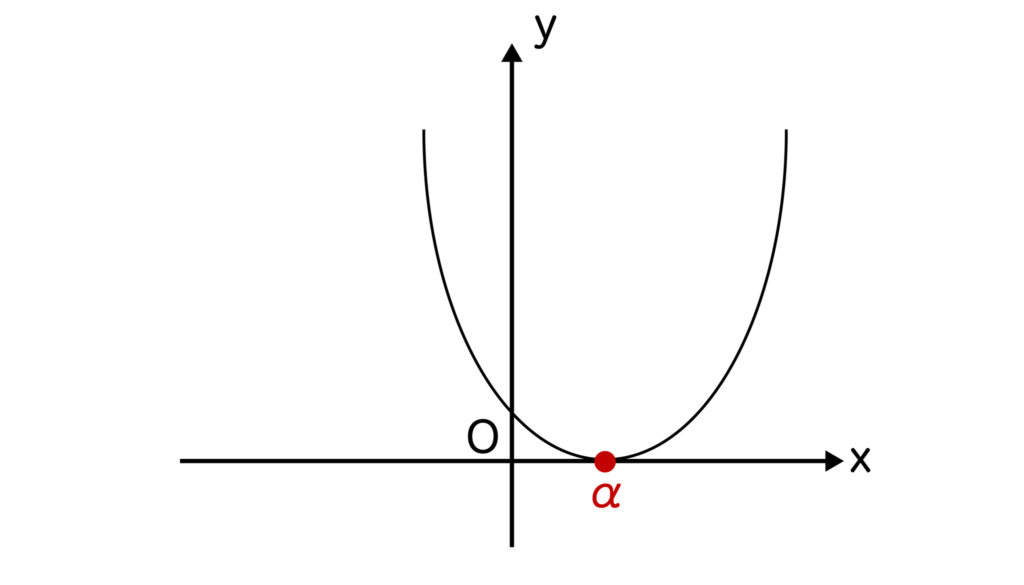
a>0より下に凸なグラフとなり、x=αの1点でx軸と接します。
※二次関数のグラフの作成方法を解説した記事もご用意しているので、ぜひ参考にしてください。
ax2+bx+c<0ということはy<0ということですね。
グラフでy<0になっているところを探してみると、y<0になっているところは1つもないことがわかります。
yの最小値はx=αのときで0になっています。y<0なので、y=0は含みません。
※記号「<」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。
よって、ax2+bx+c<0は解なしとなります。
(x-α)^2<0の解=解なし
a>0かつ判別式D=0で、二次方程式ax2+bx+c=0の重解=αということはax2+bx+cを因数分解すると(x-α)2になるということですね。
※詳しくは重解とは何かについて解説した記事をご覧ください。
つまり、(x-α)2<0はax2+bx+c<0と同じ意味ということです。
よって(x-α)2<0は解なしとなります。
ax^2+bx+c<0の解=解なし
今度はa>0かつD<0のときのax2+bx+c<0の解を考えてみます。
今回もy=ax2+bx+cのグラフを書いて考えてみましょう。
a>0、判別式D<0よりy=ax2+bx+cのグラフは以下のようになりますね。
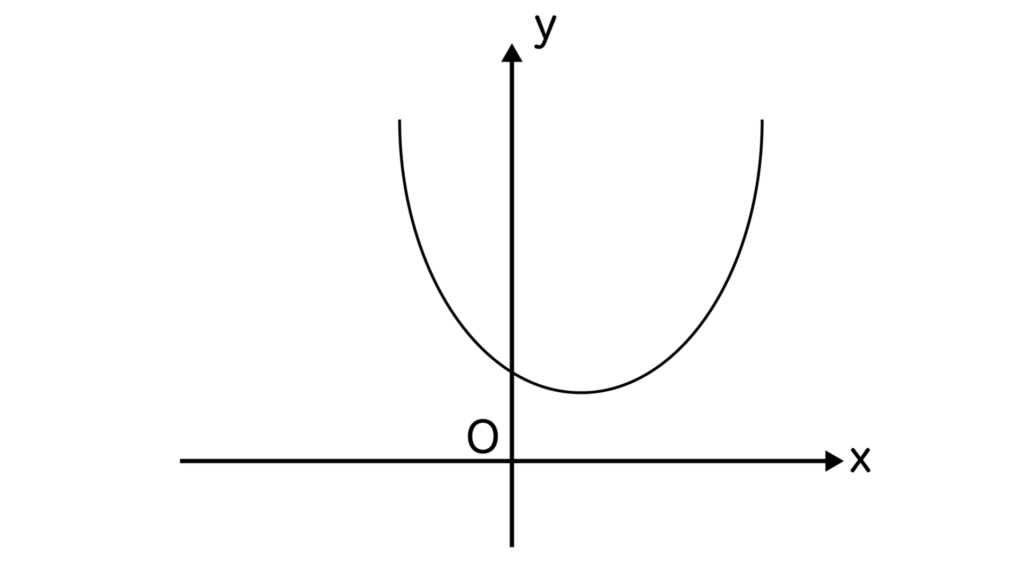
a>0なので下に凸なグラフとなり、D<0よりx軸との接点はありません。
ここで上記のグラフを見ながらax2+bx+c<0を考えてみましょう。
ax2+bx+c<0つまり、y<0となっているところはグラフに1つもありませんね。
よって、ax2+bx+c<0は解なしとなります。
ax^2+bx+c≦0の解=解なし
ax2+bx+c≦0は先ほどのax2+bx+c<0の「<」が「≦」に変わっただけです。
しかし、「≦」になっても、先ほどのグラフを見ての通りy≦0になっている箇所はありません。
「≦」なのでy=0も含みますが、判別式D<0なのでy=0になることもあり得ません。
したがってax2+bx+c≦0も解なしとなるのです。
二次不等式では解=全ての実数になるケースもある
以上で二次不等式において解なしになる4つのケースをご紹介していきましたが、二次不等式では解なしとは反対に解=全ての実数となるケースもあります。
全ての実数とは虚数(数学2で学習します)を除く全ての数が解になるということです。解なしとは真逆の意味になります。
二次方程式において解=全ての実数となるケースは「解なし」と同様に4つのケースがあります。もっと詳しく学習したい人は二次不等式の全ての実数とは?解が全ての実数になる全ケースも紹介をぜひご覧ください。
いかがでしたか?
今回は二次不等式で解なしとなる4つのケースをご紹介していきました。
二次不等式の解なしはただ単に暗記するのではなく、なぜ解なしになるのか?の理由をしっかりと理解することが重要です。ぜひ本記事を繰り返し読んで理由の部分をしっかり理解してください。


