本記事を読んでいる読者の皆様は「二次方程式とは何ですか?」と聞かれて説明できますでしょうか?
「なんとなくは理解しているけど、言葉で二次方程式を説明するのは難しいな」と感じた人も多いのではないでしょうか?
そこで今回は早稲田大学教育学部数学科を卒業した筆者が二次方程式とは何かについて解説した後、二次方程式の分野に必要な知識や公式を一挙にご紹介していきます。
高校生の皆様が二次方程式に関して知りたいであろうことを網羅している記事なので、ぜひ最後までお読みください。
二次方程式とは?簡単にわかりやすく解説
まずは二次方程式とは何かについて簡単にわかりやすく解説していきます。
二次方程式とは、最高次数が2である方程式のことです。
ここで、次数という言葉が出てきましたが皆様覚えていますでしょうか?
例えば、3x2+8x+9において、項3x2はxが2回掛け合わされているので次数=2となります。同様に考えて、項8xの次数=1、定数項9の次数=0となります。
※詳しくは多項式の定義について解説した記事をご覧ください。
なので、例えば4x+8=0という方程式は最高次数が1(=一次式)なので、一次方程式となり、x2+7x+10=0という方程式は最高字数が2(=二次式)なので、二次方程式となるわけです。
※一次式とは何かについて解説した記事もぜひ参考にしてください。
同様に考えて、例えばx3+8x-7=0という方程式は三次方程式になりますし、x6+4×2+9=0という方程式は六次方程式となります。
また「方程式」というと「右辺が0でなければならない」と思っている人も多いですが、そんなことはありません。
x2+8=3xも立派な方程式(二次方程式)です。
x2+8=3xは3xを左辺に移行すればx2-3x+8=0となり、右辺を0にできます。つまり、右辺は0にしようと思えばいつでもできるのです。
方程式と解くときは右辺を0にした方が解きやすいのでそうしていますが、必ずしも最初から右辺が0である必要はありませんのでご注意ください。
二次方程式の解き方
二次方程式の解き方としては因数分解・平方完成・解の公式の3パターンがあります。
例えば二次方程式x2-9x+20=0を因数分解・平方完成・解の公式それぞれの方法で解いてみます。
※3つの解き方の詳細は二次方程式の解き方3パターン&見分け方を徹底解説した記事をご覧ください。
【因数分解】
x2-9x+20を因数分解すると(x-4)(x-5)となるので、(x-4)(x-5)=0より、x=4、5となります。
※因数分解がわからない人は因数分解のやり方について解説した記事をご覧ください。
【平方完成】
x2-9x+20を平方完成すると、(x-9/2)2-1/4となりますね。
よって、(x-9/2)2-1/4=0となるので、-1/4を右辺に移行して(x-9/2)2=1/4とします。
すると、x-9/2=±1/2よりx=4、5となります。
※平方完成のやり方について解説した記事もぜひ参考にしてください。
【解の公式】
解の公式とは、二次方程式ax2+bx+c=0があるとき(a、b、cは実数でaは0でないとする)、その解はb2-4ac≧0のとき、x=-b±√(b2-4ac) / 2aになるという公式です。
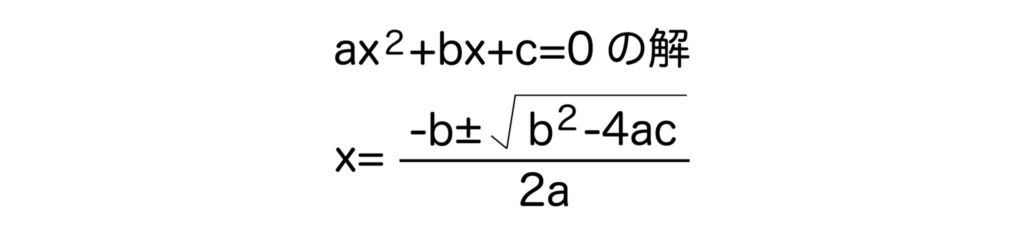
※詳しくは二次方程式の解の公式について解説した記事をご覧ください。
大学入試や共通テストでも頻出の公式なので必ず覚えましょう。
解の公式を使って先ほどの二次方程式x2-9x+20=0を解くと、
x = 9±√(-9)2-4×1×20 / 2×1 = 9±√1 / 2 = 4、5になります。
二次方程式の判別式とは?
先ほど解の公式について簡単に解説しましたが、解の公式のルートの中身であるb2-4acのことを判別式と言います。
判別式はDで表現されることが多いので覚えておきましょう。
判別式を使えば、以下のように二次方程式ax2+b+c=0の実数解の個数を調べることができます。
※実数解の意味がわからない人は実数解とは何かについて解説した記事をご覧ください。
- D>0 ⇔ 異なる2つの実数解を持つ
- D=0 ⇔ ただ1つの実数解(=重解)を持つ
- D<0 ⇔ 実数解を持たない
判別式についてもっと詳しく知りたい人は判別式とは何かについて解説した記事をご覧ください。
二次方程式の重解とは?
先ほど、「D=0 ⇔ ただ1つの実数解(=重解)を持つ」において「重解」という用語が出てきましたね。
判別式D=0となるとき、二次方程式ax2+bx+c=0は解を1つだけもち、その解のことを重解といいます。
例えば、二次方程式x2-10x+25=0の解は(x-5)2=0よりx=5の1つだけですね。つまり、5が重解となっているわけです。
このとき、判別式D=(-10)2-4×1×25より確かに0になっています。
重解という用語は二次方程式の分野においてかなりの重要用語なので必ず覚えましょう。
詳しくは重解とは何かについて解説した記事をご覧ください。
二次方程式の解と係数の関係
二次方程式では解の公式だけでなく、解と係数の関係という非常に重要な公式もあります。
二次方程式の解と係数の関係とは、二次方程式ax2+bx+c=0の解をα、βとすると
α+β=-b/a、αβ=c/a
が成り立つことです。
例えば、二次方程式3x2+6x+8=0があり、解をα、βとすると、
α+β=-6/3=-2、αβ=8/3になります。
詳しくは二次方程式の解と係数の関係について解説した記事をご覧ください。
いかがでしたでしょうか?
今回は二次方程式とは何かについて解説した後、二次方程式の学習で登場する用語や公式をご紹介していきました。
本記事でご紹介したことはすべて暗記必須の重要事項です。ぜひ何度も見返して頭に入れておきましょう。


